22. Complex Numbers Solutions Part 3

101. Since \(P, A, B\) are collinear

     \[\therefore \begin{vmatrix}z & \overline{z} & 1\\a & \overline{a} & 1\\ b & \overline{b} & 1\end{vmatrix} = 0 \Rightarrow z(\overline{a} - \overline{b}) - \overline{z}(a - b) + (a\overline{b} - \overline{a}b) = 0\]

     Similarly, \(P, C, D\) are collinear

     \[\Rightarrow z(\overline{c} - \overline{d}) - \overline{z}(c - d) + (c\overline{d} - \overline{c}d) = 0\]

     Multiplying the first equation with \(c - d\) and second with \(a - b\) and subtracting resulting equations we get

     \[z(\overline{a} - \overline{b})(c - d) - \overline{z}(\overline{c} - \overline{d})(a - b) = (c\overline{d} - \overline{c}d)(a - b) - (a\overline{b} - \overline{a}b)(c - d) \]

     Given that \(a, b, c, d\) all lie on the circle \(|z| = r \therefore |z|^2 = r^2 \Rightarrow z\overline{z} = r^2 \Rightarrow \overline{z} = \frac{r^2}{z}\)

     Substituting accordingly in previous equation

     \[z\left(\frac{r^2}{a} - \frac{r^2}{b}\right)(c - d) - z\left(\frac{r^2}{c} - \frac{r^2}{d}\right)(a - b) = \left(\frac{cr^2}{d} - \frac{dr^2}{c}\right)(a - b) - \left(\frac{ar^2}{b} - \frac{br^2}{a}\right)(c - d) \]

     Solving this will yield desired result.

102. We have,

     \[\frac{z + 1}{z - 2} = \frac{3 + t + i\sqrt{3 - t^2}}{1 + t + i\sqrt{3 - t^2}} \therefore \left|\frac{z + 1}{z - 1}\right|^2 = \frac{(3 + t)^2 + 3 - t^2}{(1 + t)^2 + 3 - t^2} = \frac{6(t + 2)}{2(t + 2)} = 3\]

     Thus modulus of required fraction is independent of \(t\).

     Also, \(z = x + iy = 2 + t + i\sqrt{3 - t^2} \Rightarrow y = 3 - (x - 2)^2\) or \((x - 2)^2 + y^2 = 3.\)

     Thus locus of complex number represents a circle with center at \((2, 0)\) having radius 3.

103. Given,

     \[\begin{vmatrix}a & b & c\\b & c & a\\c & a & b\end{vmatrix} = 0 \Rightarrow a^3 + b^3 + c^3 - 3abc = 0 \Rightarrow (a + b + c)[a^2 + b^2 + c^2 - ab -bc - ca] = 0 \Rightarrow (a - b)^2 + (b - c)^2 + (c - a)^2 = 0 \Rightarrow a = b = c [\because a + b + c \ne 0 \because z_1 \ne = 0]\]

     The circle made by these is shown below:

     

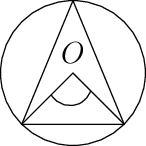
     Now OA = OB = OC where O is the origin and A, B and C are the points representing \(z_1, z_2\) and \(z_3\) respectively.

     \(\therefore\) O is the circumcenter of \(\triangle ABC.\)

     Now

     \[arg\left(\frac{z_3}{z_2}\right) = \angle BOC = 2\angle BAC = 2arg\left(\frac{z_3 - z_1}{z_2 - z_1}\right) = arg\left(\frac{z_3 - z_1}{z_2 - z_1}\right)^2\]

     Hence, proven.

104. \[z_2 = \frac{OQ}{OP}z_1e^{i\theta} = cos\theta z_1e^{i\theta} \]

     and

     \[z_3 = \frac{OR}{OP}z_1e^{i2\theta} = cos2\theta z_1e^{i2\theta} \]

     Hence,

     \[z_2^2cos2\theta = z_1z_3cos^2\theta. \]

105. Given circles are \(|z| = 1\) or \(x^2 + y^2 - 1 = 0\) and \(|z - 1| = 4\) or \(x^2 + y^2 -2x - 15 = 0.\)

     Let the circles cut by these two circles orthogonally is

     \[x^2 + y^2 + 2gx + 2fy +c = 0 \]

     Now since first two circles cut this third one orthogonally

     \[\therefore 2g.0 + 2f.0 = c - 1 \Rightarrow c = 1 \]

     and

     \[\therefore 2g(-1) + 2f.0 = c - 15 \Rightarrow g = 7 \]

     Therefore the required circles are

     \[x^2 + y^2 + 14x + 2fy + 1 = 0 |z + 7 + if| = \sqrt{48 + f^2}\]

106. Given \(|z + 3| = t^2 - 2t + 6\) represents a circle with center (-3, 0) and radius \(t^2 -2t + 6.\) The inequality \(|z - 3\sqrt{3}i| < t^2\) means \(z\) lies in the interior of circle having center at \((0, 3\sqrt{3})\) having radius \(t^2.\)

     Let A is center of first circle and B is center of second circle. Clearly when both the circles are disjoint or touching then no solution is possible.

     Further solution is left as an exercise.

107. Let \(z = x + iy\)

     \[\frac{az + b}{cz + d} = \frac{ax + iay + b}{cx + icy + d} = \frac{[(ax + b) + iay][(cx + d) - icy]}{(cx + d)^2 + d^2} Im\left(\frac{az + b}{cz + d}\right) = \frac{ay(cx + d) - cy(ax + b)}{(cx + d)^2 + d^2} \Rightarrow \frac{ady - bcy}{(cx + d)^2 + d^2}\]

     Now since \(ad > bc\) sign is same as \(y\) i.e. positive. Hence, proven.

108. Given,

     \[z_1 = \frac{i(z_2 + 1)}{z_2 - 1} \Rightarrow x_1 + iy_1 = \frac{i(x_2 + iy_2 + 1)}{(x_2 - 1) + iy_2} = \frac{[-y_2 + i(x_2 + 1)][(x_2 - 1) + iy_2]}{(x_2 - 1)^2 + y_2^2}\]

     Now equating for real part and then evaluating the desired equation will yield the result.

109. \(sin25\theta + icos25\theta\) This question is left as an exercise.

110. Let \(z = x + iy.\) Now we have

     \[z^2 + |z| = x^2 - y^2 + i2xy + \sqrt{x^2 - y^2} = 0 \]

     Equating imaginary parts we have \(2xy = 0\) which means either \(x = 0\) or \(y = 0.\) Let \(y = 0\) then we have

     \[x^2 + \sqrt{x^2} = 0 \]

     Since \(x\) is real the only possible solution is \(x = 0\). So \(z = 0.\)

     If \(x = 0\) then we have

     \[y^2 + \sqrt{-y^2} = 0 y^4 + y^2 = 0 y^2 = -1 \Rightarrow y = \pm i\]

     Thus we have \(z = \pm i.\)

111. Problem no. 111 to 118 have been left as exercises to the reader.

119. Given,

     \[|1 - \overline{z_1}z_2|^2 - |z_1 - z_2|^2 = (1 - \overline{z_1}z_2)(1 - z_1\overline{z_2}) - (z_1 - z_2)(\overline{z_1} - \overline{z_2}) [\because |z|^2 = z\overline{z}] = (1 - \overline{z_1}z_2 - z_1\overline{z_2} + |z_1|^2|z_2|^2) - (|z_1|^2 - \overline{z_1}z_2 - z_1\overline{z_2} + |z_2|^2) = (1 - |z_1|^2 - |z_2|^2 + |z_1|^2|z_2|^2) = (1 - |z_1|^2)(1 - |z_2|^2)\]

120. Consider two complex numbers \(z_1 = a_1 + ib_1\) and \(z_2 = a_2 + ib_2.\) Now we have to prove \(|z_1 + z_2| \le |z_1| + |z_2|\) which can be further extended to prove the result.

     \[\sqrt{(a_1 + a_2)^2 + (b_2 + b_2)^2} \le \sqrt{a_1^2 + b_1^2} + \sqrt{a_2^2 + b_2^2} \]

     Squaring both sides and simplifying we get

     \[a_1a_2 + b_1b_2 \le \sqrt{(a_1^2 + b_1^2)(a_2^2 + b_2^2)} \Rightarrow (a_1a_2 + b_1b_2)^2 - (a_1^2 + b_1^2)(a_2^2 + b_2^2) \le 0 \Rightarrow -(a_1b_2 - a_2b_1)^2 \le 0\]

     which is true. Hence, proven.

121. We have,

     \[\left|\frac{\overline{z_1} - 2\overline{z_2}}{2 - z_1\overline{z_2}}\right| = 1 \Rightarrow |\overline{z_1} - 2\overline{z_2}|^2 = |2 - z_1\overline{z_2}|^2 \Rightarrow (\overline{z_1} - 2\overline{z_2})(z_1 - 2z_2) = (2 - z_1\overline{z_2})(2 - \overline{z_1}z_2) \Rightarrow |z_1|^2 - 2z_1\overline{z_2} - 2\overline{z_1}z_2 + 4|z_2|^2 = 4 - 2z_1\overline{z_2} - 2\overline{z_1}z_2 + |z_1|^2|z_2|^2 \Rightarrow |z_1|^2|z_2|^2 - 4|z_2|^2 - |z_1|^2 - 4 = 0 \Rightarrow \because |z_1| \ne 1 |z_2| = 2\]

122. It can be solves similarly as 121 and is left as an exercise.

123. We have,

     \[\left|\frac{z_1 + z_2}{2} + \sqrt{z_1z_2}\right| + \left|\frac{z_1 + z_2}{2} - \sqrt{z_1z_2}\right| = \frac{1}{2}\left|(\sqrt{z_1} + \sqrt{z_2})^2\right| + \frac{1}{2}\left|(\sqrt{z_1} - \sqrt{z_2})^2\right| = |z_1| + |z_2|\]

124. From problem no. 54 it follows that \(|a + \sqrt{a^2 - b^2}| + |a - \sqrt{a^2 - b^2}| = |a + b| + |a - b|.\)

     Substituting \(a = \beta\) and \(b = \sqrt{\alpha\gamma}\) we have

     \[|\beta + \sqrt{\alpha\gamma}| + |\beta - \sqrt{\alpha\gamma}| = |\alpha|\left(|\frac{\beta}{\alpha} + \sqrt{\frac{\gamma}{\alpha}}| + |\frac{\beta}{\alpha} - \sqrt{\frac{\gamma}{\alpha}}|\right) = |alpha|\left(|-z_1 - z_2 + \sqrt{z_1z_2}| + |-z_1 - z_2 - \sqrt{z_1z_2}|\right) = |\alpha|(|z_1| + |z_2|)\]

125. We have,

     \[|a| = 1 \Rightarrow |a|^2 = 1 \Rightarrow a\overline{a} = 1 \Rightarrow \overline{a} = \frac{1}{a} \]

     From this we can write

     \[\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \overline{a} + \overline{b} + \overline{c} = 3 \]

126. Given,

     \[|z + 4| \le 3 \Rightarrow |z + 1 + 3| \le 3 \Rightarrow |z + 1| + 3 \le 3 [\because |z_1 + z_2| \le |z_1| + |z_2|] |z + 1| \le 0\]

     Following similarly

     \[|z + 4| = |z + 1 + 3| \ge |z + 1| - 3 \Rightarrow |z + 1| \ge 6 \]

     So least value is 0 and greatest value is 6.

127. Let \(z_1 = r_1cos\theta_1 + isin\theta_1\) and \(z_2 = r_2cos\theta_2 + isin\theta_2.\) Now it can be easily shown that

     \[4|z_1 + z_2|^2 - (|z_1| + |z_2|)^2\left(\frac{z_1}{|z_2|} + \frac{z_2}{|z_2|}\right)^2 \ge 0 \]

128. Given equation is \(z^2 + az + b = 0.\) Let \(p, q\) are two of its roots. Then we have \(p + q = -a\) and \(pq = b.\) Taking modulus of both we have \(|p + q| = |a|\) and \(|pq| = b.\) Now it is required that \(|p| = |q| = 1.\) Therefore we have \(|p + q| \le |p| + |q| = 2 \therefore |a| \le 2.\) Similarly \(|b| = |pq| = |p||q| = 1.\) Since \(p, q\) have unit modulii we can have them as \(p = cos\theta_1 + isin\theta_1\) and \(q = cos\theta_2 + isin\theta_2.\)

     \[pq = (cos\theta_1 + isin\theta_1)(cos\theta_2 + isin\theta_2) = cos(\theta_1 + \theta_2) + isin(\theta_1 + \theta_2) \therefore arg(b) = arg(pq) = \theta_1 + \theta_2 p + q = cos\theta_1 + isin\theta_1 + cos\theta_2 + isin\theta_2 = cos^2{\frac{\theta_1}{2}} + i^2sin^2{\frac{\theta_1}{2}} + i2sin{\frac{\theta_1}{2}}cos{\frac{\theta_1}{2}} + cos^2{\frac{\theta_2}{2}} + i^2sin^2{\frac{\theta_2}{2}} + i2sin{\frac{\theta_2}{2}}cos{\frac{\theta_2}{2}} = cos\frac{\theta_1 + \theta_2}{2} + isin\frac{\theta_1 + \theta_2}{2} \therefore arg(a) = arg(p + q) = \frac{\theta_1 + \theta_2}{2} \therefore argb = 2arga\]

129. Let \(a = x + iy.\) First we consider first two inequalities

     \[|z| \le |Re(z)| + |Im(z)| \Rightarrow \sqrt{x^2 + y^2} \le x + y\]

     Sqauting we have

     \[x^2 + y^2 \le x^2 + y^2 + 2xy \Rightarrow 2xy \ge 0 \]

     which is true. Now we consider last two inequalities

     \[|Re(z)| + |Im(z)| \le \sqrt{2}|z| \Rightarrow x + y \le \sqrt{2(x^2 + y^2)}\]

     Squaring we get

     \[x^2 + y^2 + 2xy \le 2(x^2 + y^2) \Rightarrow (x - y)^2 \ge 0 \]

     which is also true. Hence, proven.

130. Translating the given equation we have

     \[|z|^2 - 2|z| - 4 \ge 0 \]

     The greatest root of this equation is \(\sqrt{5} + 1.\) Hence proven.

131. Since \(\alpha, \beta, \gamma, \delta\) are root of the equation.

     \[(x - \alpha)(x - \beta)(x - \gamma)(x - \delta) = ax^4 + bx^3 + cx^2 + dx + e \]

     Substituting \(x = i\) we get following

     \[(i - \alpha)(i - \beta)(i - \gamma)(i - \delta) = ai^4 + bi^3 + ci^2 + di + e \Rightarrow (1 + i\alpha)(1 + i\beta)(1 + i\gamma)(1 + i\delta) = a - ib - c + id + e\]

     Taking modulus and squaring we get our desired result.

132. This is similar to 131 and is left as an exercise.

133. Let \(|z_1| = |z_2| = |z_3| = R.\) \(\therefore\) origin is the circumcenter of triangle. Since triangle is also equilateral circumcenter and origin coincide. Therefore, origin is also centroid. Thus

     \[\frac{z_1 + z_2 + z_3}{3} = 0 \Rightarrow z_1 + z_2 + z_3 = 0 \]

134. Similar to 133 it can be proven that it is an equilateral triangle. Now since \(|z_1| = |z_2| = |z_3| = 1\) therefore it is an equilateral triangle inscribed in an unit circle.

135. Circumcenter of an equilateral triangle is given by \(z_0 = \frac{z_1 + z_2 + z_3}{3}\) which is same as centroid. Now since this triangle is equilateral

     \[\sum z_1^2 = \sum z_1z_2 (\sum z_1)^2 = \sum z_1^2 + 2\sum z_1z_2 = 3\sum z_1^2\]

     Also,

     \[z_0 = \frac{\sum z_1}{3} \Rightarrow \sum z_1 = 3z_0 \Rightarrow 3\sum z_1^2 = 9z_0^2 \Rightarrow \sum z_1^2 = 3z_0^2\]

136. Since \(z_1, z_2\) and origin form an equilateral triangle we have

     \[z_1^2 + z_2^2 + 0^2 - z_1z_2 - z_2*0 - z_1*0 = 0 \]

     Hence, proven.

137. From 136 \(z_1, z_2\) and origin will form a triangle if \(z_1^2 + z_2^2 - z_1z_2 = 0.\) Therefore,

     \[(z_1 + z_2)^2 = 3z_1z_2 \Rightarrow a^2 = 3b. \]

138. Centroid of the triangle is given by \(\frac{z_1 + z_2 + z_3}{3}\) i.e. \(\frac{-3\alpha}{3}\) i.e. \(-\alpha.\) Triangle will be equilateral if

     \[z_1^2 + z_2^2 + z_3^2 = z_1z_2 + z_2z_3 + z_3z_1 \Rightarrow (z_1 + z_2 + z_3)^2 = 3(z_1z_2 + z_2z_3 + z_3z_1) \Rightarrow 9\alpha^2 = 9\beta \Rightarrow \alpha^2 = \beta\]

139. Given,

     \[z_2 = \frac{z_1 + z_3}{2} \]

     Clearly, from section formula we can deduce that \(z_2\) divides line segment joining \(z_1\) and \(z_3\) in two equal segments hence the complex numbers are collinear.

140. \(z_3\) will divide line segment joining \(z_1\) and \(z_2\) either externally or internally. Now section formula can be used to prove remaining.

141. We have,

     \[\frac{z - i}{ z + i} \]

     as a purely imaginary quantity. Let \(z = x + iy.\)

     \[\frac{[x + i(y - 1)][x - i(y + 1)])}{x^2 + (y + 1)^2} \]

     Equating real part to 0 we have

     \[\Rightarrow x^2 + y^2 - 1 = 0 \]

     Therefore locus of z represents the circle \(x^2 + y^2 = 1.\)

142. \(z\) represents the ring between the concentric circles whose center is at (3, 4i) having radii 1 and 2.

143. Let \(z = x+ iy.\) Now we have

     \[\sqrt{(x - 1)^2 + y^2} + \sqrt{(x + 1)^2 + y^2} \le 4 \]

     Let \(L + M = 4\)

     \[L^2 - M^2 = -4x \therefore L^2 - M^2 = -x \therefore 4L^2 = (4 - x)^2 4(x^2 + y^2 - 2x + 1) = 16 + x^2 - 8x 3x^2 + 4y^2 = 12 \frac{x^2}{4} + \frac{y^2}{3} = 1\]

     Hence it represent the above ellipse.

144. Let \(z = x + iy\) then we have

     \[x = t + 5 \text{ and } y = \sqrt{4 -t^2} \Rightarrow (x - 5)^2 = t^2 \text{ and } y^2 = 4 -t^2\]

     Adding we get, \((x - 5)^2 + y^2 = 4\) which represents a circle with radius at (5, 0) with radius 2.

145. Given \(\frac{z^2}{z - 1}\) is real i.e. its imaginary part is zero.

     \[\frac{(x^2 - y^2 + i2xy)((x - 1) - iy)}{(x - 1)^2 + y^2} \]

     Equating imaginary part to 0 we have

     \[x^2 + y^2 - 2x = 0 \therefore (x - 1)^2 + y^ = 1 \]

     which represents a circle having center at (1, 0) and radius unity.

146. Given, \(|z^2 + (-1)| = |z|^2 + |(-1)| \Rightarrow \frac{z^2}{-1}\) is non-negative real number. Thus \(z\) is purely imaginary number. Thus locus of z is a straight line.

Question 147 to 149 are left as exercises.

150. Given,

     \[\log_{\sqrt{3}}\frac{|z|^2 - |z| + 1}{2 + |z|} < 2 \Rightarrow \frac{|z|^2 - |z| + 1}{2 + |z|} < (\sqrt{3})^2 \Rightarrow |z|^2 - 4|z| - 5 < 0 \Rightarrow |z| < 5\]