1. Introduction#
First thing first. Definitely this is not the only book on data structures and algorithms. There are many great books on the subject. I will mention few of those. No links to any online shop will be given as it will show my bias towards that store. The first book is the most authoritative book on the subject which treats topics in great depth. It is the “The Art of Computer Programming” by Donald E. Knuth. The book is available in several volumes. Volume 1 describes Fundamental Algorithms, 2 describes numerical algorithms, 3 details sorting and searching and 4A deals with combinatorial algorithms. As of now only these volumes have been published. But these books are not for weak hearted people and I really mean that. This series is very heavy on mathematics and implementation is done using a computer designed by Knuth MMIX. However, it is a must read for advanced readers. The second book is also a classic. It is “Introduction to Algorithms” written by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein. This book is also known as “CLRS”. While Knuth is very deep, this book covers topics in breadth. Once again an excellent book but examples are given in pseudo programming language. There are many other introductory books on this subject with little difference in quality and almost all of them are a good read.
The subject of this book is data structure and algorithms. That involves three words. Data, structure and algorithms. A computer stores and manipulates data i.e. information. We use computer to store, manipulate and use data. We present same information in many ways which is about structure. The data and structure determines that what kind of operations i.e. algorithms can be performed over them. For example, we cannot perform addition on two character strings but then we can concatenate them using + operator in an object-oriented language which support operator overloading. Thus, these words summarize the soul of computer programming and software. All programs which we use and all operations we do involve these three basic elements.
Oh you would say that I missed the word mathematics. Well, then you have been observant! That was deliberate. :) Mathematics which will be treated in this book is although separate from the main subject but certain portions of the book like computer graphics and computational geometry will require a great deal of mathematics. Certainly the mathematics part can form a new book and can be read as such in isolation but I am a fan of thicker books so I intend to make it thick. Since I have no intention of getting it printed that, is all good. Such is miracle of digital technology.
There are specific structures which facilitate specific operations. For example, a stack allows access of data only from top. A queue is helpful to realize a life-like queue. A linked list allows traversal in forward or backward or both directions but not random. Binary trees are helpful for faster searches. Graphs can be used for path-finding and to solve network problems. Hash maps are very good for finding information quickly. These are just few cases which I have cited. The area of data structures and algorithms is immense and ever expanding.
This book is a natural successor of my first book on C99 programming. Examples will include only knowledge from C99 book.
1.1. Problem to Solution#
Usually while programming you will face the situation when you have to write a program to solve a problem. You will end up using few data structures and a few algorithms to solve that program. This book describes the most common data strutures and algorithms which have evolved over several centuries of mathematical work by mathematicians. Given a problem we build a model of solution (read program) in our mind. The details of that mental model varies from individual to individual. Once that mental model is built our brains orientation is fixed to a certain way of thinking. Now because of this we choose certain data structures and algorithms and try to find out solution using data starutures and algorithms chosen. Sometimes we are successful other times we fail may be partially maybe fully. Now the most important thing when we fail is to think over the problem again and get a fresh thinking. So better take a break. This is most serious advice I can give. Whenever you have difficulty solving a problem for more than 30 minutes take a break. This will reset your thinking and allow you to think in new way and you can try to find the solution afresh.
1.2. Abstract Data Types#
While code is definitely the final goal, to reach there we make models in our
mind. For example, when we think of numbers as humans we can think of numbers
without the restriction of range but in case of computers we are constrained by
the amount of memory available. However, that does not stop us from making
abstract models because typically computers have enough memory available for
storing large enough numbers available for all practical purposes. An abstract
data type specifies the logical properties of a data type. As you know a data
type like int, char and float represent collection of values and these
types determine what operations can be performed on those types. For example,
you should not perform multiplication on characters although programmatically it
is possible, it just does not make sense. Although, other meanings are possible
to multiplication to a character or string i.e. repetition but certainly not
multiplication. Thus, the collection of values and operations form an abstract
mathematical entity that can be implemented using hardware and software. This is
what is known as abstract data type. A formal way to put what an ADT is class
of objects whose logical behavior is defined by a set of values and a set of
operations. From experience I know that beginners do not really care for ADTs
and they simply skip to the implementation part which is not good. Unless you
understand the concept at an abstract level you will not be able to appreciate
the semantics of the ADT and as a result your implementation may suffer.
When we define an abstract data type we do not worry about efficiency whether time or space. Since it is abstract therefore those worries come when we implement that. While defining an ADT, we are not worried about implementation details. Certain times it may be possible to implement our ADT on a piece of hardware or software system. For example, infinitely big numbers or strings cannot be implemented in hardware or software as said earlier because of memory limitations. But then again for all practical purposes an ADT will be useful as help while implementing our problem provided you are willing to maintain the semantics.
There are two main ways of defining an ADT, imperative and functional. Imperative way of defining an ADT is closer to programming languages like C, C++ etc which allow imperative programming techniques while functional style is better suited for functional languages like Erlang, Haskell, OCaml etc. However, I will deviate from the formal style a bit to make it easy for you to understand ADTs without knowledge of a programming language so that you can evaluate it as a mathematical model.
Let us consider an example ADT then we will dissect that after:
ADT UnsignedInteger
Object: An ordered subrange of integers starting at zero and ending at a
maximum value of UINT_MAX on the computer.
/* operations */
for all x, y in N(set of natural numbers) and true, false in booleans
true ::== 1 (UnsignedInteger)
false ::== 0 (UnsignedInteger)
Zero(): UnsignedInteger => 0
IsZero(x): Boolean => if(x == 0) IsZero = true else false
Add(x, y): UnsignedInteger => if(x + y < UINT_MAX) Add = x + y
else Add = (x + y)%(UINT_MAX + 1)
Equal(x, y): Boolean => if (x == y) Equal = true else false
Sub(x, y): UnsignedInteger => if(x > y) Sub = x - y
else Sub = positive of 2's complement
with MSB is not sign bit
Mul(x, y): UnsignedInteger => if((x * y) < UINT_MAX) Mul = x * y
else Mul = (x * y)%(UINT_MAX + 1)
Div(x, y): UnsignedInteger => Div = Quotient of x/y
Mod(x, y): UnsignedInteger => Mod = Remainder of x/y
You, my observant reader, would have noticed that this is not an ADT in its purest sense because we have cared about hardware i.e. assumed that it implements 2’s complement. Your observation is correct. It is not an ADT but I have tried to make sure that this ADT works on modern computers which work on 2’s complement. Certainly this will not work on systems like UNIVAC which implement 1’s complement in hardware.
However, that is not important part. The important part is to learn as how you
specify an ADT so that it works. Let us try to learn what has been described in
ADT. This ADT describes unsigned integers much like that found in a statically
typed language like C or C++. This ADT starts at 0 and ends at a specific value
specified by UINT_MAX. What would be UINT_MAX is not specified as an
optimum value of that depends in internal details of hardware. Zero() is an
operation which always returns zero. IsZero() is an operation which returns
true if argument is zero else false. true and false have been specified
as their typical Boolean notations of 1 and 0 respectively. Add() adds two
unsigned integers if their sum is less than UINT_MAX, if it is more than
that then it is rotated which is based on the behavior of hardware again. Now I
leave it up to you to figure rest of ADT.
1.2.1. An ADT for rational numbers#
To foster the ideas as how to represent an ADT let us consider another example of rational numbers. A rational number is a fraction which either terminates or repeats upon division for example, \(\frac{1}{2}, \frac{3}{7}, \frac{7}{9}\). Thus, we see that denominators and numerators are integers. We also have to consider the sign of these rational numbers, which, may be positive or negative which we will represent using character data type for example. For completeness let us define a minimalistic character abstract data type as well.
ADT Character
Object: A character on English PC-104 keyboard which can fit in 8 bits
character ::== a-z,A-Z,0-9,`~!@#$%^&*()-_=+[{]}\|;:'",<.>/?(space)(TAB)(return)
c is one of the characters being one of the above.
value(c): UnsignedInteger => if(c == a-z)
return 0-25
else if(c == A-Z)
return 26-51
else if(c == 0-9)
return 52-61
else
sequential value in above list
from remaining characters
I have kept the ADT character minimalistic to be enough to serve our typical
usage. (space) specifies the space bar on your keyboard while (TAB) is
the tab and (enter) is the return key. We have defined characters in terms
of integral value so that we can store it in memory because memory can contain
only sequence of bits. Characters really cannot be stored in memory as it
is. This will allow us to apply equality for two characters as well as other
operations which can be applied to integers though I have left them for you as
an exercise. First three commas are just field separators.
Let us define our rational number ADT now.
ADT Rational
Object: A rational number which has a finite denominator and numerator.
/* Operations */
for all n1, n2, d1 and d2 as UnsignedInteger with d1 != 0 and d2 != 0
and true and false are our usual Booleans.
s1 and s2 are signs represented as Character - and +.
rational ::== <numerator, denominator, sign> where numerator and denominator
are UnsignedInteger, denominator != 0 and sign is a character '+' or '-'
MakeRational(n, d, s): Rational => return <n, d, s>
IsEqual(n1, d1, s1, n2, d2, s2): Boolean => if((n1*d2 == n2*d1) &&
((s1 == s2 == '+')||(s1 == s2 == '-')))
return true
else return false
Greater(n1, d1, s1, n2, d2, s2): Rational => if( s1 == s2)
if((n1*d2) >(n2*d1))
return <n1, d1, s1>
else if(s1 == '+')
return <n1, d1, s1>
return <n2, d2, s2>
Add(n1, d1, s1, n2, d2, s2): Rational => if(s1 == s2)
return <(n1*d2 + n2*d1),
d1*d2, s1>
else if(Greater(n1, d1, s1, n2,
d2, s2) == <n1, d1, s1>)
return <(n1*d2 - n2*d1),
d1*d2, s1>
else
return <(n2*d1 - n1*d2),
d1*d2, s2>
Sub(n1, d1, s1, n2, d2, s2): Rational => if(s1 == s2)
return <(n1*d2 - n2*d1),
d1*d2, s1>
else if(Greater(n1, d1, s1, n2,
d2, s2) == <n1, d1, s1>)
return <(n1*d2 + n2*d1),
d1*d2, s1>
else
return <(n2*d1 + n1*d2),
d1*d2, s2>
Mul(n1, d1, s1, n2, d2, s2): Rational => if(s1 == s2)
return <n1*n2,
d1*d2, '+'>
else
return <n1*n2,
d1*d2, '-'>
Div(n1, d1, s1, n2, d2, s2): Rational => if(s1 == s2)
return <n1*d2,
d1*n2, '+'>
else
return <n1*d2,
d1*n2, '-'>
It is not at all hard to understand the rational number ADT and I think that it is self-explanatory. I have used this informal style of ADT description for now but when I will be describing data structures I will stick to a more formal style.
One particular operation I would like to point out is IsEqual operation. Usually
ADTs are equal when they have equal value but in case of rational numbers they can be
equal even if absolute fractions are not equal. Rather, the different fractions will
have equal value in their reduced form, for example, \(\frac{1}{2}, \frac{2}{4},
\frac{3}{6}\).
Now that we have learned small bits of how to define an ADT let us turn our attention to more important philosophical questions.
1.2.2. Advantages of ADTs#
1.2.2.1. Encapsulation#
An ADT guarantees the properties and operations about itself. This allows programmer of ADT that only so much is needed to satisfy the requirements posed by ADT. The implementation may be complex but that is abstracted by a very simple interface definition. Thus, a great deal of abstraction is achieved by specifying the ADT for the user of ADT. As a programmer of ADT we are worried only about satisfying the interface and properties requirements of ADT and nothing more.
1.2.2.2. Localization of Change and Isolation from Implementation#
As a user of ADT we are not worried if the implementation changes internally as long as ADTs’ interface does not change. Since the implementation must adhere to interfaces defined by the ADT in question we as user of ADT get a guarantee that we are isolated from the implementation. Thus, a change in implementation of ADT does not warrant a change in our code as ADT user. For example, a car’s accelerator, break and clutch are always in the same positional order irrespective of change of mechanics inside. As you can see that changes in implementation are localized to the implementation details and users of the ADT are not effected which allows decoupling of ADT implementation and its usage which results in parallel work on both sides.
1.2.2.3. Flexibility#
An ADT can be implemented in different ways as you will see soon when I will present implementation of queues and stacks both using an array and a linked list. However, the users of those queues and stacks are free to switch between the two implementations as they see fit because the interfaces of ADTs remain same. This allows us to use different implementations as per requirement of our problem giving us flexibility and efficiency.
1.2.3. Complexity Considerations for an ADT#
As I have said that while defining an ADT, we are not worried about performance criterion of implementation. However, there are two schools of thoughts. One faction thinks that these should not be part of ADT while the other thinks that ADT should guarantee a minimum on performance criterion in terms of memory and time. For example, I will quote the author of STL, Alexander Stepanov who puts forth his argument as:
Following is what Alexander Stepanov has to say:
As far as I think complexity considerations should be part of ADTs because based on these guarantees we can choose what we will use and what we will not. In that sense, you can say that I agree with the opinion of Stepanov. In our trivial ADTs which we have seen I have omitted the complexity considerations but before we can include complexity considerations we have to include those in our analysis. However, before we can really introduce complexity considerations in our ADTs we have to learn what is complexity and how do we evaluate that. But before we can learn how to compute complexity of an algorithm let us have a concrete definition for it.
1.3. What is an Algorithm?#
The word algorithm comes from the name of the 9th century Persian Muslim mathematician Muḥammad ibn Mūsā al-Khwārizmī. Algorism originally referred only to the rules of performing arithmetic using Hindu-Arabic numerals but evolved via European Latin translation of al-Khwārizmī’s name into algorithm by the 18th century. al-Khwārizmī wrote a book titled “On the Calculation with Hindu Numerals” in about 825 AD, and was principally responsible for spreading the Indian system of numeration throughout the Middle East and Europe. It was translated into Latin as “Algoritmi de numero Indorum” (in English, “Al-Khwarizmi on the Hindu Art of Reckoning”). The term “Algoritmi” in the title of the book led to the term “algorithm”. Usage of the word evolved to include all definite procedures for solving problems or performing tasks. The question is a what is an algorithm. An algorithm is a finite sequence of well-defined operations on some input data which produces an output in finite amount of time and requires finite amount of space to hold its data which can be presented in a well-defined formal language for evaluation of a function.
The concept of algorithm has existed for millennia, however a partial formalization of what would become the modern algorithm began with attempts to solve the Entscheidungsproblem (the “decision problem”) posed by David Hilbert in 1928, who was a great mathematician born in Prussia(modern Russia). Coincidently, John Von Neumann(father of modern computer architecture and inventor of merge sort) was his assistant for some time. The geniuses of Hilbert and Neumann is well known. Hilbert’s problems which is a list of 23 problems have fueled much of mathematical research of 20th century while Neumann contributed to development of computers, nuclear bombs both Uranium and Hydrogen bombs as well as towards development of ICBMs. Subsequent formalizations were framed as attempts to define “Effective calculability”, those formalizations included the Gödel–Herbrand–Kleene recursive functions, Alonzo Church’s lambda calculus, Emil Post’s “Formulation 1”, and Alan Turing’s Turing machines. We will study Lambda Calculus and Turing Machines later in this book.
Algorithm A (Euclid’s algorithm). Given two positive integers a
and b find the greatest common divisor, i.e. the largest positive
integer which evenly divides (remainder after division is 0) both a
and b.
A1. [Find remainder.] Divide a by b. Say r is remainder
(r will certainly be \(0\le r<b\).).
A2. [Is it zero?] If r = 0 terminate execution b is the GCD.
A3. [Exchange values.] Set a = b and b = r. Goto step A1.
I will use the word A for alorithm. This algorithm will have a monotonically increasing suffix which will be a positive integer. When these algorithms are later referenced a hyperlink will be made to refernce back to the algorithm.
Some algorithms will have flowcharts given for them. For example, given below is the flowchart for Euclid’s algorithm.

Euclid’s algorithm as a flowchart.
Let us see a C99 program which evaluates GCD of two numbers. Given below is the sample code.
#include <stdio.h>
int main()
{
int a=0, b=0, r=1;
printf("Enter two positive integers separated by space:\n");
scanf("%d %d", &a, &b);
while(r != 0) {
r = a % b;
if(r == 0)
break;
else {
a = b;
b = r;
}
}
printf("GCD is %d\n", b);
return 0;
}
Note that terminating condition for our program is that remainder becomes zero. Typically we initialize variables with value 0 in C99 but in this case it must be non-zero. Now let us look at some desirable properties of an algorithm.
1.4. Complexity of an Algorithm#
There can be several algorithms to achieve the same effect on a particular set of data. However, the two methods may have different requirements on time constraint. One may take more or less or equal time than the second one. We definitely always want an algorithm which consumes less time. Time may not be only contraint all the time. Sometimes we may be bound by amount of memory available to use. This may forbid us from using those algorithms which consume more memory even though they run faster. So there are two types of complexities which are in question time and space.
Before we proceed let us familiarize ourselves with some special functions of mathematics and mathematical constants:
Function |
Name |
Typical Value |
Approximation |
|---|---|---|---|
\(\lfloor x\rfloor\) |
floor function |
\(\lfloor 3.14\rfloor\) |
\(x\) |
\(\lceil x\rceil\) |
ceiling function |
\(\lceil 3.14\rceil\) |
\(x\) |
\(\log_2 N\) |
binary logrithm |
\(\log_2 1024 = 10\) |
\(1.44\ln N\) |
\(F_N\) |
Fibonacci Numbers |
\(F_{10} = 55\) |
\(\phi^N/\sqrt{5}\) |
\(H_N\) |
Harmonic Numbers |
\(H_{10} = 2.9\) |
\(\ln N = \gamma\) |
\(N!\) |
Factorial Function |
\(10! = 3628800\) |
\((N/e)^N\) |
\(\log N!\) |
Logrithm Function |
\(\log 100! = 520\) |
\(N\log N - 1.44N\) |
Given below are some constants:
Constant |
Value |
|---|---|
\(e\) |
\(2.71828...\) |
\(\gamma\) |
\(0.577211...\) |
\(\phi\) |
\(\frac{1+ \sqrt{5}}{2}\) |
\(\ln 2\) |
\(0.693147...\) |
\(\log e\) |
\(1/\ln 2=1.44269...\) |
If we consider harmonic sequence defined by the equation
\(H_N = 1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{N}\)
then it looks like following curve for definite integral \(\ln N = \int_x^N \frac{dx}{x}\)
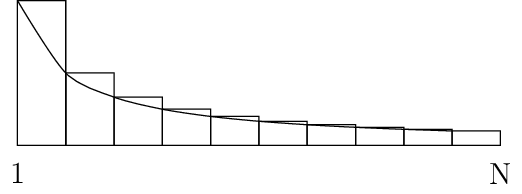
Harmonic Series Representation
As you can see the harmonic sequence is defined by the total area of the bars in the image while logarithm natural is the area under curve. The formula
\(H_N \approx \ln N + \gamma + (1/12 N)\)
is a very good approximation for the harmonic sequence where \(\gamma\) is Euler–Mascheroni constant also known Euler’s constant after Swiss mathematician Leonhard Euler. Lorenzo Mascheroni was an Italian mathematician.
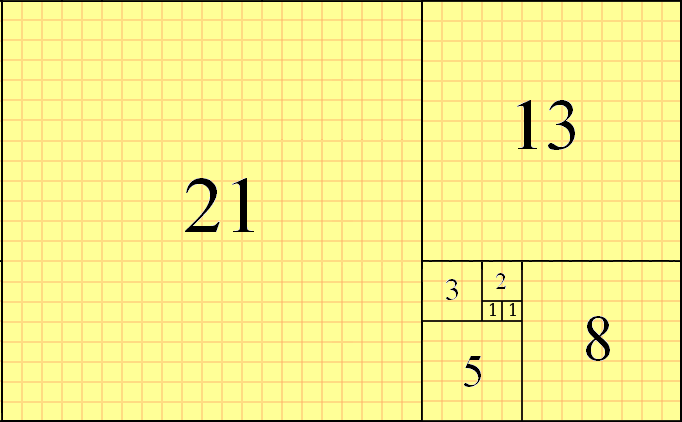
Similarly, for Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 … the nth term is represented by the recurrence relation \(F_N = F_{N_1} + F_{N-2}\) for \(N \ge 2\) where \(F_0 = 1\) and \(F_1 = 1\). These Finonacci numbers have many interesting properties. Fibonacci series also occurs in nature. For example, have a look at the following image of yellow Chamomile(courtesy, Wikipedia):

In this picture, the yellow Chamomile is showing the arrangements in 21(blue) and 13(aqua) spirals. Similarly, the sunflower image for its seeds also depict similar arrangements as shown below:

A geometrical representation of Fibinacci numbers can be given by golden spiral.
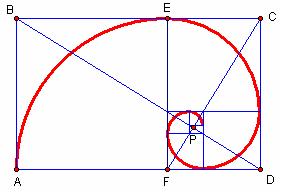
The sizes of squares are 1, 1, 2, 3, 5, 8, 13, 21 and 34. The spiral converges at the intersection of the two blue lines (P), and the ratio of the lengths of these two lines BP: PD is \(phi\), the Golden Ratio. In geometry, a golden spiral is a logarithmic spiral whose growth factor is the golden ratio. The polar equation for a golden spiral is the same as for other logarithmic spirals, but with a special value of the growth factor \(b: r = ae^{b\theta}\). An alternative image is given below(countesy Wikipedia1):
Another occurrence of Fibinacci number is in rose petals as shown below:

There are two ways by which you can categorize complexity. The first categorization is by resource consumption. We measure these using consumption of memory and CPU. Memory consumption is known as space complexity and CPU consumption is known as time complexity. The second categorization is by the methods by which we measure complexity of an algorithm. One of the popular methods is Big-O notation denoted by \(O\) . Big-O notation focuses on upper bound of algorithms for huge sets of data(tending to be infinity) and thus is known as asymptotic complexity. Another method which is less popular is amortized complexity. Amortized complexity is not concerned about worst-case performance but rather average run time for all cases. In an algorithm an operation may be costly but then its frequency may be less. Amortized complexity takes care of this fact and tries to balance the complexity value. Thus, we can safely say that Big-O notation is a guarantee but amortized notation is a probabilistic way of deducing run-time or rather more practical notion. Since it is much easier to computer Big-O complexity we will focus on it but from time to time I will also introduce amortized complexity for analysis of algorithms where suitable. Unfortunately, it is much harder to compute average case complexity or amortized complexity. To computer average case complexity one must make assumption about distribution of input which may not match with realistic inputs and realistic inputs are not easily represented as mathematical model. On the other hand worst-case complexity is quite acceptable and is universally acceptable but a paper by Paul Kemp shows that what can go wrong with worst case complexity. Note that worst case complexity comes in picture for very large inputs thus an algorithm demonstrating better worst case complexity is not necessarily better algorithm for real-world programs.
Big-O is a member of a larger family of notations that is called Landau notation, Bachmann–Landau notation (after Edmund Landau and Paul Bachmann). Mathematically it tells us that how closely a finite series approximates a given function, especially for a truncated Taylor series or asymptotic expansion.
One more concept is there for classification of algorithms. This classification is based on the fact whether data is available in its entirety to the algorithm or not. If the algorithm requires that data must be available for algorithm to work then it is known as offline algorithm. Algorithms which do not require entire data to be available on work on part of data at a point of time are known as online algorithms. Clearly as you can fathom, online algorithms will have better performance that offline algorithms. If ratio of performance of an online algorithm and its counterpart offline algorithm is bounded, the online algorithm is called competitive. Also, a point worth noticing is that all online algorithms do not have an offline counterpart.
Now let us try to understand what is big-O notation and how to compute it. Consider two functions \(f(x)\) and \(g(x)\). Let us assume that these functions operate on a subset of real numbers. Then in big-O notation \(f(x)\) is written in terms of \(g(x)\) as follows:
if and only if there is a positive constant \(K\) such that for all sufficiently large values of \(x,~f(x)\) is at most K multiplied by \(g(x)\) in absolute value. That is, \(f(x)~=~O(g(x))\) if and only if there exists a positive real number \(K\) and a real number \(x_0\) such that
We typically do not say that we are concerned with growth rate as \(x\) goes to \(\infty\) and we simply write \(f(x) = O(g(x))\).The notation can also be used to describe the behavior of \(f\) near some real number \(a\) (often, \(a = 0\)): we say
if and only if there exist positive numbers \(\delta\) and \(K\) such that
If \(g(x)\) is non-zero for values of \(x\) sufficiently close to \(a\), both of these definitions can be unified using the limit superior:
if and only if
To explain how we compute \(O(n)\) let us see an example. Consider a polynomial function with all positive coefficients. Say our polynomials is somthing like \(f(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + ... + a_{n-1}x + a_n\). We can very safely say
Therefore we can say \(f(x) = O(x^n)\).
1.4.1. An Alternative Definition#
For two functions \(f(x)\) and \(g(x)\) and a constant \(K \in I\!R^+\) \(f(x) = O(g(x))\) if \(lim_{x\rightarrow \infty} \left(\frac{g(x)}{f(x)}\right) = K\)
Given below is a plot of some most common functions encountered in algorithms.
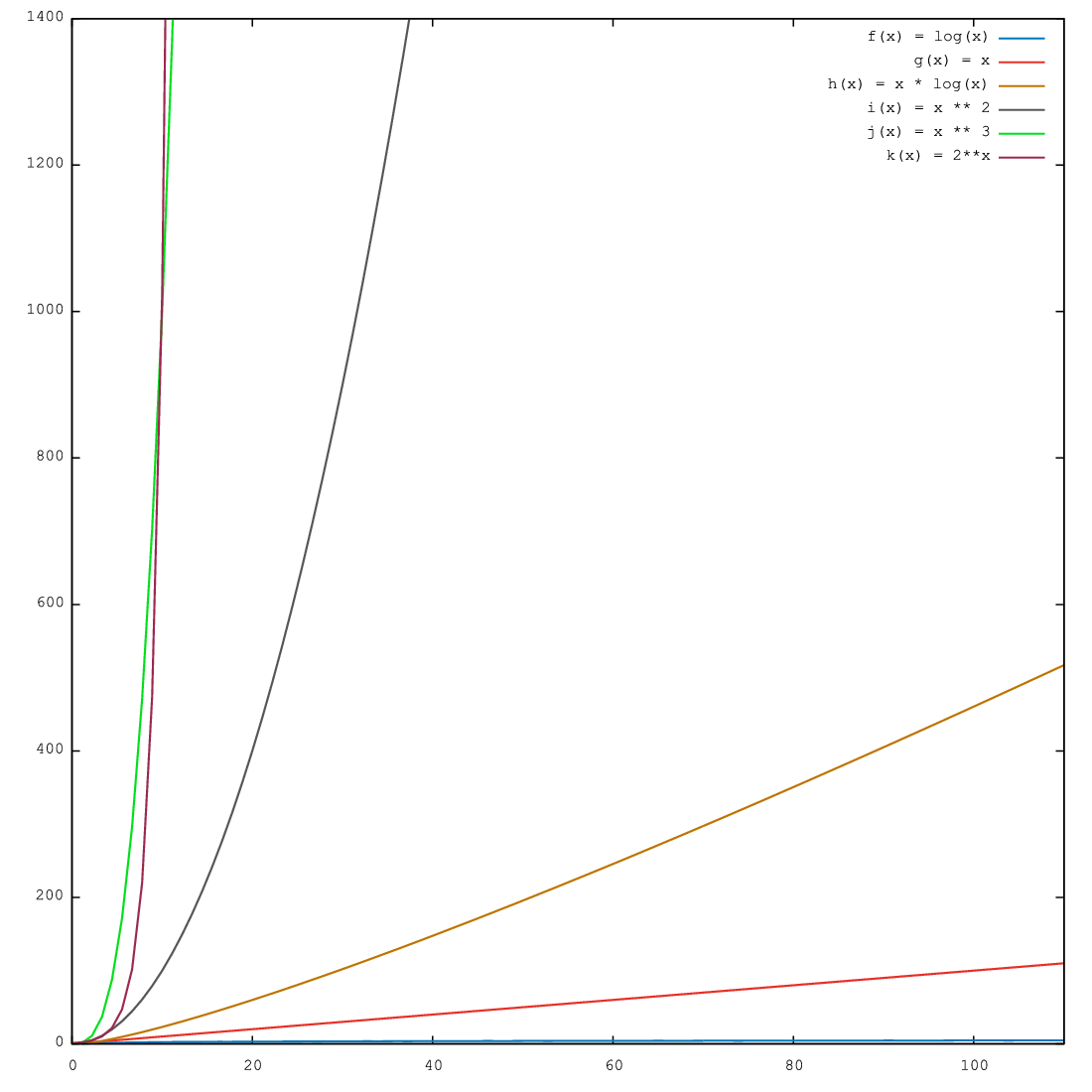
Note that plot of log(x) is barely visible in output. As you can clearly
see \(log(x)<x<x*log(x)<x^2<x^3<2^n\).
As \(O\) -notation gives upper bound similarly \(\Omega\) -notation gives lower bound.
\(g(n) = \Omega(f(n))\) means there exists two constants \(L\) and \(n_0\) such that
\(g(n) \ge L|f(n)|\) for all \(n> n_0\).
If we want to write exact order of growth without being accurate about constant factors \(L\) and \(K\) then we use \(\Theta\) -notation.
\(g(n) = \Theta(f(n)) \Leftrightarrow g(n) = O(f(n))\) and \(g(n) = \Omega(f(n))\) implying \(\Theta\) -notation gives both upper and lower bounds.
In computer science for algorithm analysis we are almost always worried about big-\(O\) complexity because it gives upper bound i.e. for large set of input how the algorithm will behave.
Complexity of algorithms form into various functions. I am presenting graphs of some common functions below for quick understanding. By looking at these graphs you can quickly deduce that which complexity fares well and which does not.
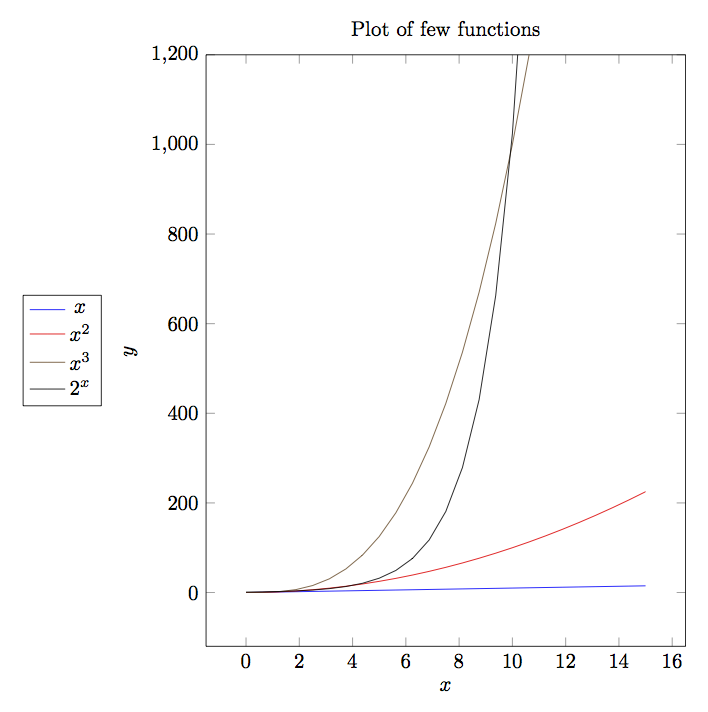
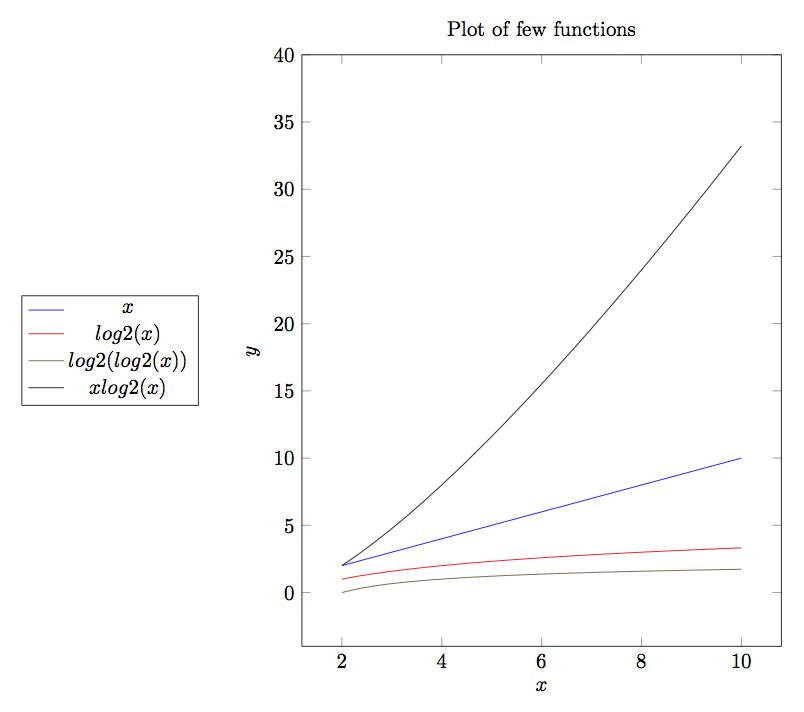
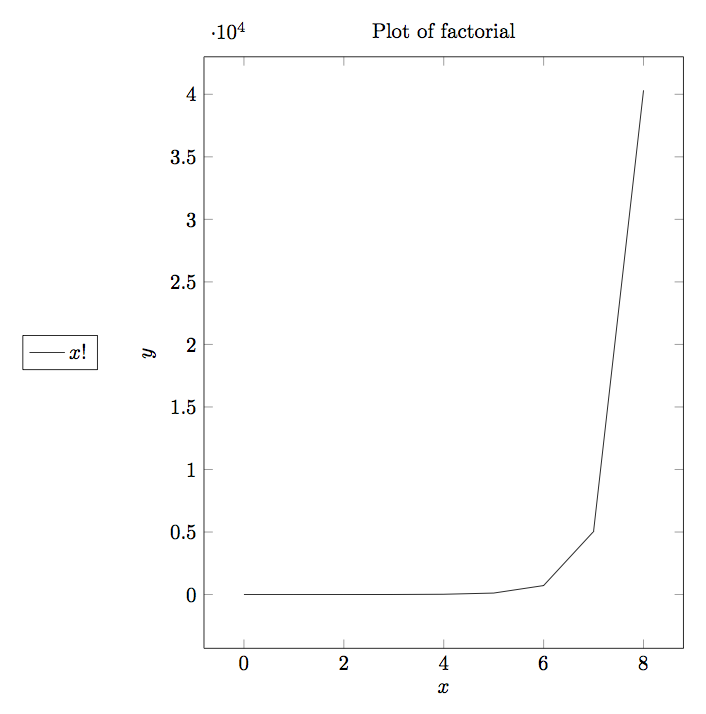
Continuing this let us discuss a bit more about big-\(O\) notation. The problem with big-\(O\) notation is that even though it talks about two contants \(x_0\) and \(K\) it does not give any hints about there values or how to compute them. It also does not put any restriction on the values of these constants not gives any guidelines when there are many such values.
There is also space efficiency or memory efficiency. There are times when the devices we use do not have a lot of memory then we need to find algorithms which are efficient memory-wise. For example, there are two very good algorithms for sorting an array of values (or string) quick sort and merge sort. However, consider the case when we have less memory than the array then neither of these algorithms can be used. One of the sorting algorithms among many is external sort. This technique is old because in earlier devices memory was less and usually data to be sorted was more.
I am presenting a table for runtime of various complexities, looking at which you can appreciate the algorithms with better runtime. This table is for a computer which executes instructions at \(10^9\) instructions per second.
\(x\) |
\(f(x)=x\) |
\(f(x)=x\log_2 x\) |
\(f(x)=x^2\) |
\(f(x)=x^3\) |
\(f(x)=2^x\) |
|---|---|---|---|---|---|
10 |
.01 μs |
.03 μs |
.1 μs |
1 μs |
1 μs |
20 |
.02 μs |
.09 μs |
.4 μs |
8 μs |
1 ms |
30 |
.03 μs |
.15 μs |
.9 μs |
27 μs |
1 s |
40 |
.04 μs |
.21 μs |
1.6 μs |
64 μs |
18.3 min |
50 |
.05 μs |
.28 μs |
2.5 μs |
125 μs |
13 d |
100 |
.1 μs |
.66 μs |
10 μs |
1 ms |
4* \(10^{13}\) yrs |
1000 |
1 μs |
9.96 μs |
1 ms |
1 s |
32* \(10^{283}\) yrs |
10,000 |
10 μs |
130 μs |
100 ms |
16.67 min |
|
100,000 |
100 μs |
1.66 ms |
10 s |
11.57 days |
|
1,000,000 |
1 ms |
19.92 ms |
16.67 min |
31.71 yrs |
The complexity of function \(2^x\) rises so fast that it is already beyond the number of years sun is going to survive. As you can clearly see \(O(log(log(x)))O(log(x))<O(x)<O(x*log(x))<O(x2)<O(x3)<O(2x)<O(x!)\). As O-notation gives upper bound similarly Ω-notation gives lower bound. g(x)=Ω(f(n)) means there exists two constants L and \(n_0\) such that
\(g(x)\ge L|f(x)| ~\forall~ x>x_0\)
Note that this is Knuth’s definition for \(\Omega\) not the Hardy-Littlewood definition. Knuth has commented on why he has changed this definition:
Hardy-Littlewood’s version of \(\Omega\) is given below:
\(f(x)=\Omega(g(x))\;(x\rightarrow\infty)\;\Leftrightarrow\;\limsup_{x\rightarrow\infty}\left|\frac{f(x)}{g(x)}\right|>0\)
If we want to write exact order of growth without being accurate about constant factors \(L\) and \(K\) then we use \(Θ\) - notation.
\(g(x)=\Theta(f(x))\Leftrightarrow g(x)=O(f(x)) ~\text{and}~ g(x)=\Omega(f(x))\)
Note that for an algorithm performing at a complexity of \(O(x^2)\) we can say that \(O(x3)\) is its complexity as an approximation. It is allowed to represent a complexity at a worse notation but not a better notation. Just that the statement will be slightly inaccurate. The reason for this is that the function which has worse complexity is still and upper bound of the better function and thus our assumption of giving an upper bound holds true.
If you know calculus and coordinate geometry then you would notice that a worse function has a higher rate of growth i.e. slope of the curve i.e. \(\frac{dy}{dx}\) or \(\frac{df(x)}{dx}\) where \(y=f(x)\). For any higher value of \(x\) the slope or rate of growth will eventually be higher for worse performing function. For example, for \(O(x^2)\) that value of \(x\) is 1 when compared with \(O(x)\). This value can be obtained by solving \(\frac{dy}{dx}\) for the two functions.
In computer science for algorithm analysis we are almost always worried about big-\(O\) complexity because it gives upper bound i.e. for large set of input how the algorithm will behave. The problem with big-\(O\) notation is that even though it talks about two constants \(x_0\) and \(K\) it does not give any hints about there values or how to compute them. It also does not put any restriction on the values of these constants not gives any guidelines when there are many such values.
There is also space efficiency or memory efficiency. There are times when the devices we use do not have a lot of memory then we need to find algorithms which are efficient memory-wise. For example, there are two very good algorithms for sorting an array of values (or string) quick sort and merge sort. However, consider the case when we have less memory than the array then neither of these algorithms can be used. One of the sorting algorithms among many is external sort. This technique is old because in earlier devices memory was less and usually data to be sorted was more. Algorithms which were very important a few decades ago are now important merely for academic importance.
In case you prefer graphs to mathematical functions to understand, below I present all three big notations.
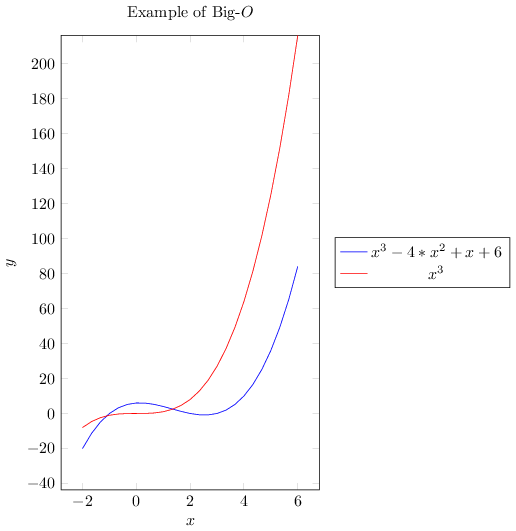
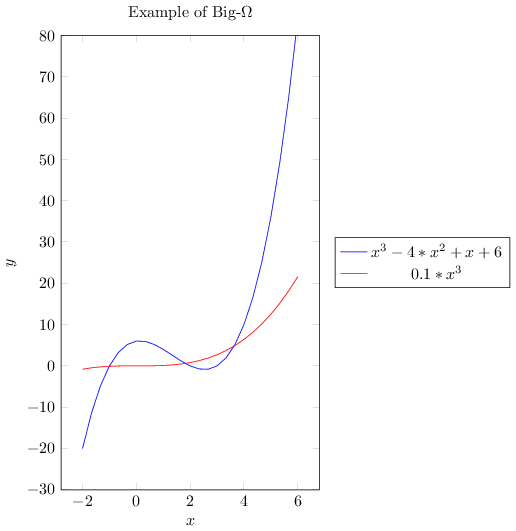
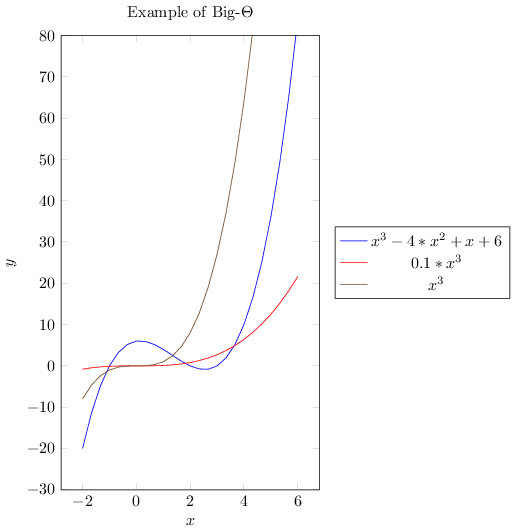
1.5. Examples of Asymptotic Complexity Computation#
In an algorithm analysis we have to consider all operations although many times
if the code is simple you can just see and guess the complexity. However, in
case of complex code you will find it difficult to do that. For example
consider the following code which computes sum of n numbers stored in an
array.
for(i=sum=0; i<n; ++i)
sum += a[i];
First we have two initializations for i and sum. Let cost of assignment
be \(C_1\). Then i is incremented from 0 to n-1. Let cost of
increment be \(C_2\). Now There are n additions and n assignments
for sum. Let cost of addition is \(C_3\). So total cost is
\(n*(C_1 + C_3)\). Thus total cost is \(2*C_1 + n*C_2 + n*(C_1 + C+3)\)
i.e. \((2+n)C_1 + n*C_2 + n*C_3\). These constants \(C_1, C_2\) and
\(C_3\) can be measured in terms of clock cycles. Thus complexity is
\(O(n)\).
As you can guess if we have nested loops complexity wil increase in terms of power of \(n\). However, the complexity may not increase exactly by integral power.
1.6. Simplicity#
It is not enough for an algorithm to be efrficient from the perspective of memory and time but it should also be simple enough to implement. For example, splay-trees are very good for maintaining fast search time. But the implementation is complex compared to a Red-Black tree or AVL-tree therefore they are usually not preferred. However, this is not the only reason. I will let you know more detail when we discuss trees in their own chapter.
1.7. More on Asymptotic Notations#
1.7.1. Little o Notation#
The notation is written as \(f(x)=o(g(x))\). And in set notation it is \(f(x)\in o(g(x))\). It means that \(g(x)\) grows faster than \(f(x)\). As \(x\rightarrow\infty\) for every positive constant \(\epsilon\) there exists a constant \(x\) such that
\(\vert f(x)\vert\leq\epsilon\vert g(x)\vert\;\forall\;x\geq N\)
Note the difference between big-O and little-o. While for big-O we need at least one constant but for little-o it must hold true for all constants, however small. Thus, the constraints for little-o is stronger than big-O. This also implies a function which is big-O will be little-o but may not be other way around.
If \(g(x)\) is nonzero, or at least becomes nonzero beyond a certain value of its variable, the relation \(f(x)=o(g(x))\) is equivalent to
\(\lim_{x\rightarrow\infty}\frac{f(x)}{g(x)}=0\)
1.7.2. Little \(\omega\) Notation#
Little-\(\omega\) notation is the inverse of the little-\(o\) notation i.e.,
\(f(x)\in o(g(x))\Leftrightarrow g(x)=\omega f(x)\)
\(\lim_{x\rightarrow\infty}\frac{g(x)}{f(x)}=0\)
1.8. Problems on Complexity#
For each of the following pairs of functions \(f(n)\) and \(g(n)\), either \(f(n) = O(g(n))\) or \(g(n) = O(f(n))\), but not both. Determine the case.
\(f(n) = (n^2 - n)/2, g(n) = 6n\).
\(f(n) = n + 2\sqrt{n}, g(n) = n^2\).
\(f(n) = n + \log n, g(n) = n\sqrt{n}\).
\(f(n) = n\log n, g(n) = n\sqrt{n}/2\).
\(f(n) = n + \log n, g(n) = \sqrt{n}\).
\(f(n) = 2(\log n)^2 , g(n) = \log n + 1\).
\(f(n) = 2(\log n)^2 , g(n) = \log n + 1\).
\(f (n) = 4n \log n + n, g(n) = (n^2 - n)/2\).
Which of the following cases are true and which are false?
\(n^2 = O(n^3)\).
\(n^3 = O(n^2)\).
\(n\log n = O(n\sqrt{n})\).
\(\sqrt{n} = O(\log n)\).
\(\log n = O(\sqrt{n})\).
\(n^3 = O(n^2(1 + n^2))\).
\(1/n = O(\log n)\).
\(\log n = O(1/n)\).
\(\log n = O(n^{-1/2})\).
If \(f(n) \sim g(n)\), then \(f(n) = \Theta(g(n))\).
If \(f(n) = \Theta(g(n))\), then \(g(n) = \Theta(f(n))\).
Give proof for following:
Does \(n^{\log n} = O((\log n)^n)\)?
Does \(n^{\log n} = \Omega((\log n)^n)\)?
Does \(n^{\log \log \log n} = O((\log n)!)\)?
Does \(n^{\log \log \log n} = \Omega((\log n)!)\)?
Does \((n!)! = O(((n - 1)!)!(n - 1)!^{n!})\)?
Does \((n!)! = \Omega(((n - 1)!)!(n - 1)!^{n!})\)?
Does
\[O\left(\left(\frac{n^2}{\log \log n}\right)^{1/2}\right) = O(\lfloor\sqrt{n}\rfloor)\]Does \(2^{(1+O(1/n))} = 2 + O(1/n)\).
Prove that if \(f_1(n) = O(g_1(n))\) and f_2(n) = O(g_2(n)), then \(f_1(n) + f_2(n) = O(g_1(n) + g_2(n))\).
Prove that if \(f_1(n) = \Omega(g_1(n))\) and f_2(n) = Omega(g_2(n)), then \(f_1(n) + f_2(n) = O(g_1(n) + g_2(n))\).
Prove that if \(f_1(n) = O(g_1(n))\) and f_2(n) = O(g_2(n)), then \(f_1(n) + f_2(n) = O(max\{g_1(n), g_2(n)\})\).
Prove that if \(f_1(n) = \Omega(g_1(n))\) and f_2(n) = Omega(g_2(n)), then \(f_1(n) + f_2(n) = \Omega(min\{g_1(n), g_2(n)\})\).
Prove or disprove: For all functions \(f(n)\) and \(g(n)\), either \(f(n) = O(g(n))\) or \(g(n) = O(f(n))\).
Prove or disprove: If \(f(n) > 0\) and \(g(n) > 0\) for all \(n\), then \(O(f(n) + g(n)) = f(n) + O(g(n))\).
Prove or disprove: \(O(f(n)^{\alpha}) = O(f(n))^{\alpha}\) for all \(\alpha \in \mathbf{R^+}\).
Prove or disprove: \(O(x + y)^2 = O(x^2) + O(y^2)\).
1.9. Mathematical Induction#
Mathematical induction is a powerful technique to prove certain mathematical equalities and inequqlities. To analyze an algorithm we can use mathematical induction. There will be many times when analyzing an algorithm mathematical induction will come handy. Many of the readers may be familiar with it and many may not. Therefore, I will start with basics of this particular technique. We will then develop some basic formulas to be used in this book. We use mathematical induction technique in following way.
Given a statement \(S(n)\) we first prove \(S(1), S(2)\) and \(S(3)\) are true. We then assume \(S(k)\) is true. After that we prove \(S(n+1)\) to be true. After this we can draw conclusion that \(S(n)\) is true for all \(n\).
Consider a statement that
now if we have to prove this then we will perform following step:
Algorithm A1
A1.1 Prove for \(S(1)\)
A1.2 Prove for \(S(2)\)
A1.3 Assume \(S(k)\) to be true.
A1.4 Prove \(S(k+1)\) to be true.
Therefore for step A1.1 \(S(1) = 1 = \frac{1*2}{2}\). So \(S(1)\) is true. For step A1.2 \(S(2) = 1 + 2 = 3 = \frac{2*3}{2}\). Now \(S(2)\) is also true. Let us say
now \(S(k+1) = k*(k+1)/2 + k+1 = (K+1)*(k+1+1)/2\). Hence, by mathematical induction we have proven the statement.
Therefore we can draw following flowchart for mathematical induction.
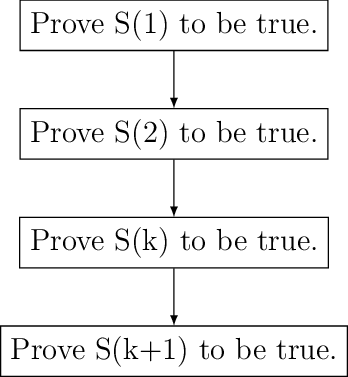
Flowchart for mathematical induction.
Let us consider another simple example which will further help boost our foundations of mathematical induction.
Consider a statement saying
Now we first find \(S(1) = 1 = 1^2\) which is true. For \(n = 2\) we have \(S(n) = 1 + 3 = 4 = 2^2\). Now let us assume it is true for \(k\). Now let us try for \(k+1\). \(S(k+1) = k^2 + 2k + 1 = (k+1)^2\). Therefore, we have proven the series to be true for \(S(n)\).
You can visualize this using a geographical representation too. I would like to ask the reader to find the visual diagram as an exercise.
1.10. Some Basic Mathematics#
Let us see a way to find sum of first \(n\) numbers. Typically we use symbol \(\sum\) to denote the sum. The following notations are used.
\(\sum_{1\le i\le n}i\), \(\sum_{1\le i\le n}a_i\) and \(\sum_{i=0}^na_i\) to denotes the sum of numbers 1 to \(n\) and series \(a_1+a_2+a_3+...+a_n\) respetively.
Let us try to find sum of first \(n\) numebers using another method which will not use mathematical induction.
The same can be written by reversing the series in following manner
Now if we sum the series we will get following
So now we can clearly get our result mentioned in the above section.
Before we proceed let us take a look at following solution:
Now by the same analogy let us try to find out sum of squares.
There is one more generic notation \(\sum_{R(i)}a_i\). Here, \(R(i)\) is any relation which involves \(i\). The notation here means sum of all \(a_i\) for \(i\) for which relation \(R(i)\) is true. Now let us study some basic laws with this notation.
Distributive Law, for multiplication of such sums:
For example consider the follwing case:
Interchanging order of summation:
The reader is to prove this. This is left as an exercise.
Change of variable:
Hacking the relation:
Given these four rules reader is encouraged to find the sum an arithmetic and an geometric progression.
I think I should stop here now and ask the reader to brush up his math skills. These derivations are just a glimpse of what you will need to analyze the algorithms.