2. Recursion#
In this chapter we will study recursion. Recursion is such a powerful concept that it requires its own chapter. Usually, beginners find it hard to understand recursion. We will study several problems and their solutions to foster the concept of recursion. We will also study advantages and disadvantages of recursion. I have already discussed recursion in small detail here. Usually, beginners do not understand recursion because they do not understand how the stack(not the data structure but the stack of a process in memory) works. Once you understand how it works, it is very easy to understand recursion. I will treat recursion in much greater depth here than what was presented in C programming book.
The power of recursion can be understood by following quote by great computer scientist Nicklaus Wirth:
Formally, we can say that a definition, which defines an object in terms of simpler case of itself is recursive definition. In C or any other programming language for that matter, recursion is the concept of a function calling itself. When a repeated operation has to be preformed over a variable, recursion can be used. Recursion simplifies the code a lot. Typically, there is always a more effective iterative solutions are available but there are certain cases where recursion is always better than iteration. For example, traversal of trees where iteration is not so effective as compared to recursion. For beginners it is hard to understand recursion but once you understand it then it is not that hard to understand. A classic example is that of factorial calculation which would serve as base of the entire concept. The formula for factorial is given by \(n! = \prod_{k = 1}^nk\) and recursive definition of factorial is given by: \(n! = 1\) if \(n = 0 n!=(n - 1)! * n~~\forall~~n > 0\)
In case you do not understand the formula given below is expansion:
\(0! = 1! = 1\)
\(n! = \prod_{k=1}^n = n \times (n - 1) \times (n - 2) \times ... 3 \times 2 \times 1\)
However, note that last two equations are not recursive. Rather, the one given in terms of \((n-1)!\) is recursive because it defines factorial in terms of a factorial in a simplified form.
A recursive definition usually have one or more base cases, which produce result without causing recurrence for one or more set of inputs in a trivial fashion. Obviously, recursive algorithm also have recursive cases, where the algorithm recurs i.e. calls itself. For example, for factorial definition the base case would be \(0!=1\). The recursive case for factorial is \((n-1)!\) Note that you have to be very careful when writing recursive algorithms in any structured language because the stack is limited and deep recursion will cause stack overflow. However, there are techniques like tail recursion described below which allows you to do deep recursion. Usually, base cases are when the recursive algorithm terminates and thus, these are called terminating cases.
Sometimes you may not really have a terminating or base case. For example, evaluation of \(e^x = 1 + x +
\frac{x^2}{2!} + \frac{x^3}{3!} + ...\) or \(\cos(x) = 1 - x + \frac{x^2}{2!} - \frac{x^3}{3!} + ...\) does not
really have a base case. For evaluation of such infinite series you have to settle on an error constant usually denoted
by \(\epsilon\) up to which you compute the series and then you stop. Usually if the constant \(\epsilon\) is
below six significant digits for float and twelve for double then you should stop calculation as that is the
maximum resolution you will get. The constant factor \(\epsilon\) will determine the terminating case for such a
series.
2.1. Types of Recursion#
2.1.1. Single and Multiple Recursions#
Recursions involving single references are known as single recursion and those involving multiple references are known as multiple recursion. For example, the factorial definition which we have seen is a case of single recursion. An example of multiple recursion is Fibonacci sequence. Mathematically an nth Fibonacci number in sequence is given by \(F_n + F_{n - 1} + F_{n - 1}\) while the first two numbers are given by \(F_1 = F_2 = 1\). Since the recursion involves two simpler references that is why we call it multiple reference. Another such example would be Ackermann’s function. Ackermann’s function is given by
Clearly, second and third cases of Ackermann’s function show that it is a function having multiple recursion. One more important example of multiple recursion is traversal of binary tree in all three ways i.e. in-order, pre-order and post-order. Similarly, depth-first traversal of a graph is also a classic example of recursion. We will not see these last two here but rather in their own respective chapters of trees and graphs.
Sometimes, it is possible to convert a multiple recursion algorithm to single recursion version. For example, a naive implementation of Fibonacci sequence shown above will be a case of multiple recursion but we can save two numbers and generate next Fibonacci number and pass it along with the previous number to the next iteration which will cause multiple recursion to become single recursion and will also allow us to do tail recursion. When we do this it becomes a case of corecursion. Similarly, binary tree can be traversed using extra storage iteratively or you can use threaded binary tree to eliminate the need of that extra storage.
2.1.2. Indirect Recursion#
The examples which we have seen are cases of direct recursion. In direct recursion a function calls itself. However,
if is quite possible for two functions to call each other. When such calls happen then the functions are known as
demonstrating indirect recursion or mutual recursion. It is quite possible that a function f calls another
function g and then g calls f again. Chains of more than 2 functions is also possible. For example, a
function f1 calls functions f2 which in turn calls f3 and then it calls f1.
Two very good examples of indirect or mutual recursion are recursive descent parsers and finite state machine implementation. For a recursive descent parser each rule of the grammar can be implemented as a function and these functions can call each other. A finite state machine’s individual states can be implemented by a separate function and while the states keep changing these functions can call each other forming a case of indirect recursion i.e. mutual recursion.
2.1.3. Anonymous Recursion#
Our programming language is C and in ISO C11(as of this writing. It may be part of a future specification with something like block of Obj-C.) this does not happen but I am giving this for the sake of completeness of discussion of recursion. Usually functions recurse by calling themselves by name. But in certain languages there are functions known as anonymous functions or lambdas which do not have a name. When such functions recurse then it is known as anonymous recursion. However, untill I give C++ examples you will not see this in action in this book.
2.1.4. Structured and Generative Recursion#
A classification has been made by authors on how a piece of data is generated and used by certain authors. There are two types of such categorization. First is structured and second is generative.
Thus a critical observation which we can have from this definition is that the type of argument is a simpler form of original input following our original definition of recursion. For example, parsing an XML document or a JSON document, any kind of tree traversal will fall in this category. Even factorial or single recursive version of Fibonacci sequence generation will fall in this category.
The second category is defined as:
The critical difference between these two types of recursion is how they terminate. Where it is very easy to prove the termination of structurally recursive functions, it is much harder to do so for generative recursions. The guarantees of simplification of data in generative recursion is harder to guess. When you want to give a mathematical proof for structurally recursive function the proof is easier to give because the complexity decreases uniformly, usually but it may be non-uniform for generative recursion and thus, making it harder to give a proof.
2.2. Tail Recursion#
Functional languages usually do not have loops. In such languages a loop is written using recursion. For example,
consider the following loop which prints all positive integers for data type unsigned long.
#include <stdio.h>
#include <limits.h>
int main()
{
for(unsigned long i=0; i<=ULONG_MAX; ++i)
printf("%lu\n", i);
return 0;
}
If you observe this simple program then it start printing the sequence 0, 1 ,2 till ULONG_MAX is reached and then it
will wrap around and i will become zero and loop will terminate. This simple loop can be implemented using recursion
as shown below:
void f(unsigned long i)
{
if(i == ULONG_MAX) {
printf("%lu\n", i);
return;
}
printf("%lu\n", i);
f(i + 1);
}
int main()
{
f(0);
return 0;
}
If I compile this program using the command gcc -Wall -std=c11 -pedantic test.c then it causes stack overflow and
terminates at a value of 261938 for i. The reason is simple is and that is it creates a lot of stack frames which is
limited by ulimit. I can make my stack size more than its current valeu of 8MB but that is not the solution because
even with all the RAM i.e. 8GB on my computer that willl be exhausted by this code. Now, the question is how do we
overcome this problem. The short answer is that you add -O2 to compiler for compilation making the command
gcc -Wall -std=c11 -pedantic test.c. This will make code work. The long answer is that when you pass -O2 flag to
compiler then it does tail recursion optimization. Before we go in detail about tail recursion optimization let us look
at assembly produced by the steps gcc -Wall -std=c11 -pedantic -c test.c and objdump -d test.o respectively:
test.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <f>:
0: 55 push %rbp
1: 48 89 e5 mov %rsp,%rbp
4: 48 83 ec 10 sub $0x10,%rsp
8: 48 89 7d f8 mov %rdi,-0x8(%rbp)
c: 48 83 7d f8 ff cmpq $0xffffffffffffffff,-0x8(%rbp)
11: 75 18 jne 2b <f+0x2b>
13: 48 8b 45 f8 mov -0x8(%rbp),%rax
17: 48 89 c6 mov %rax,%rsi
1a: bf 00 00 00 00 mov $0x0,%edi
1f: b8 00 00 00 00 mov $0x0,%eax
24: e8 00 00 00 00 callq 29 <f+0x29>
29: eb 26 jmp 51 <f+0x51>
2b: 48 8b 45 f8 mov -0x8(%rbp),%rax
2f: 48 89 c6 mov %rax,%rsi
32: bf 00 00 00 00 mov $0x0,%edi
37: b8 00 00 00 00 mov $0x0,%eax
3c: e8 00 00 00 00 callq 41 <f+0x41>
41: 48 8b 45 f8 mov -0x8(%rbp),%rax
45: 48 83 c0 01 add $0x1,%rax
49: 48 89 c7 mov %rax,%rdi
4c: e8 00 00 00 00 callq 51 <f+0x51>
51: c9 leaveq
52: c3 retq
0000000000000053 <main>:
53: 55 push %rbp
54: 48 89 e5 mov %rsp,%rbp
57: bf 00 00 00 00 mov $0x0,%edi
5c: e8 00 00 00 00 callq 61 <main+0xe>
61: b8 00 00 00 00 mov $0x0,%eax
66: 5d pop %rbp
67: c3 retq
and the counterpart produced by gcc -Wall -std=c11 -pedantic -O2 -c test.c and objdump -d test.o is given below:
test.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <f>:
0: 48 83 ff ff cmp $0xffffffffffffffff,%rdi
4: 53 push %rbx
5: 48 89 fb mov %rdi,%rbx
8: 74 24 je 2e <f+0x2e>
a: 66 0f 1f 44 00 00 nopw 0x0(%rax,%rax,1)
10: 48 89 da mov %rbx,%rdx
13: 31 c0 xor %eax,%eax
15: be 00 00 00 00 mov $0x0,%esi
1a: bf 01 00 00 00 mov $0x1,%edi
1f: 48 83 c3 01 add $0x1,%rbx
23: e8 00 00 00 00 callq 28 <f+0x28>
28: 48 83 fb ff cmp $0xffffffffffffffff,%rbx
2c: 75 e2 jne 10 <f+0x10>
2e: 5b pop %rbx
2f: 48 c7 c2 ff ff ff ff mov $0xffffffffffffffff,%rdx
36: be 00 00 00 00 mov $0x0,%esi
3b: bf 01 00 00 00 mov $0x1,%edi
40: 31 c0 xor %eax,%eax
42: e9 00 00 00 00 jmpq 47 <f+0x47>
Disassembly of section .text.startup:
0000000000000000 <main>:
0: 48 83 ec 08 sub $0x8,%rsp
4: 31 ff xor %edi,%edi
6: e8 00 00 00 00 callq b <main+0xb>
b: 31 c0 xor %eax,%eax
d: 48 83 c4 08 add $0x8,%rsp
11: c3 retq
The key is the bottom of functions at locations 4c and 42 respectively. As you can see in the first version callq
instruction is called to call the function which is our recursive call but it is simply not their in optimized
version. The question is how compiler can deduce. If you look at carefully call of function f(0) has no dependency on
the values computed by f(1), which has no further dependency on f(2) and so on. Thus the compiler can optimize in such a
way that no new stack frames need to be created for further calls. But even before we tail recursion in more detail, let
us try to capture what how recursive code is executed in terms of stack. I am giving an indicative diagram for that
below:

As you can see when main calls f(0) a stack frame is created and again for f(1) and again for f(2) and
it will continue untill all of stack is exhausted or i becomes equal to ULONG_MAX. Let us say we had infinite
stack memory available to us then when i reaches the base case of ULONG_MAX then f(ULONG_MAX) will return
and successively f(ULONG_MAX - 1) and others will follow in reverse order. This is known as stack unwinding.
However, since we do not have infinite space available to us we need to use tail recursion. The fundamental principal
behind tail recursion is that we should write in code in such a way that later calls of our function are not a
dependency for earlier calls i.e. caller does not have a dependency on callee. If we can ensure that then compiler will
be able to optimize that for us. This example was a trivial example. More involving recursive examples will have more
complicated versions of tail recursive functions. Note that functional languages deploy tail recursion heavily to
optimize their code execution. Tail recursion not only makes deep recursion possible but causes less consumption of
memory. For example, you can increase your stack size to 1GB if you have enough RAM available by using the command
ulimit -s 1048576. Then run the unoptimized version of binary and examine the memory usage which will go on
increasing till the stack space is violated. There is no computer in this world which can run the unoptimized version of
the program. The benefit is not only of memory. Even execution of a tail recursive version will be faster because it
takes time to set up stack frames however small that is. It will matter for large stack sizes and deep recursion. Even
the instruction call to call a function is expensive, relatively.
Now I will present several recursive algorithms, evaluate their complexity, give implementations for both naive version and tail recursive version.
2.3. Recursive Algorithms#
2.3.1. Factorial Computation#
I straightaway present recursive implementation of factorial computation. First a naive version.
//Description: Recursive factorial.
#include <stdio.h>
long long fact(unsigned int input);
int main()
{
unsigned int input=0;
printf("Enter a number whose factorial has to be computed:\n");
scanf("%u", &input);
printf("Factorial of %u is %lld.\n", input, fact(input));
return 0;
}
long long fact(unsigned int input)
{
if(input==0)
return 1;
else
return fact(input-1)*input;
}
The problem with this implementation can be seen from the fact that compiler cannot optimize it for tail recursion. This can be seen from the assembly given below:
test.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <fact>:
0: 53 push rbx
1: 89 fb mov ebx,edi
3: b8 01 00 00 00 mov eax,0x1
8: 85 db test ebx,ebx
a: 75 04 jne 10 <fact+0x10>
c: 5b pop rbx
d: c3 ret
e: 66 90 xchg ax,ax
10: 8d 7b ff lea edi,[rbx-0x1]
13: e8 00 00 00 00 call 18 <fact+0x18>
18: 48 0f af c3 imul rax,rbx
1c: 5b pop rbx
1d: c3 ret
Thus we will have to modify our code in the way we have discussed so that compiler can do necessary optimization. The improved version is given below:
#include <stdio.h>
void factorial(unsigned int *index, unsigned int *input, unsigned long long *fact);
int main()
{
unsigned int input = 0;
unsigned int index = 1;
unsigned long long fact = 1;
printf("Enter a number whose factorial has to be computed:\n");
scanf("%u", &input);
factorial(&index, &input, &fact);
printf("Factorial of %u is %llu.\n", input, fact);
return 0;
}
void factorial(unsigned int *index, unsigned int *input, unsigned long long *fact)
{
if(*index == *input) {
return ;
}
else {
*index += 1;
*fact *= *index;
}
factorial(index, input, fact);
}
and the equivalent assembly of our function is:
test.o: file format elf64-x86-64
Disassembly of section .text:
0000000000000000 <factorial>:
0: 8b 07 mov (%rdi),%eax
2: 3b 06 cmp (%rsi),%eax
4: 74 1d je 23 <factorial+0x23>
6: 48 8b 0a mov (%rdx),%rcx
9: 0f 1f 80 00 00 00 00 nopl 0x0(%rax)
10: 83 c0 01 add $0x1,%eax
13: 41 89 c0 mov %eax,%r8d
16: 89 07 mov %eax,(%rdi)
18: 49 0f af c8 imul %r8,%rcx
1c: 39 06 cmp %eax,(%rsi)
1e: 75 f0 jne 10 <factorial+0x10>
20: 48 89 0a mov %rcx,(%rdx)
23: f3 c3 repz retq
As you can see that factorial has been optimized for tail recursion. It may appear from above code that I have
bypassed base case but it is not so. That is hidden in the way variables are initialized. fact is initialized with 1
which guaranteed that even for input having a value 0 our result is 1 and same for input having a value 1. Thus
base cases are implicit in code.
2.3.2. Fibonacci Series#
First I present the most naive version using multiple recursion which then I will convert quickly to single recursion and then present a tail recursive version.
Naive Version
#include <stdio.h>
long long fibonacci(int input);
int main()
{
int input=0;
printf("Which Fibonacci number you want?\n");
scanf("%d", &input);
printf("%lld\n", fibonacci(input));
return 0;
}
long long fibonacci(int input)
{
long long fib1=1, fib2=1;
if(input==1)
{
return fib1;
}
else if(input==2)
{
return fib2;
}
else
{
long long fib = fibonacci(input-1)+fibonacci(input-2);
return fib;
}
}
What is wrong? Well, it is terribly wrong. Consider following diagrams for function calls for different Fibonacci
numbers(number inside circles indicate the position of that number in sequence and corresponding fib call):
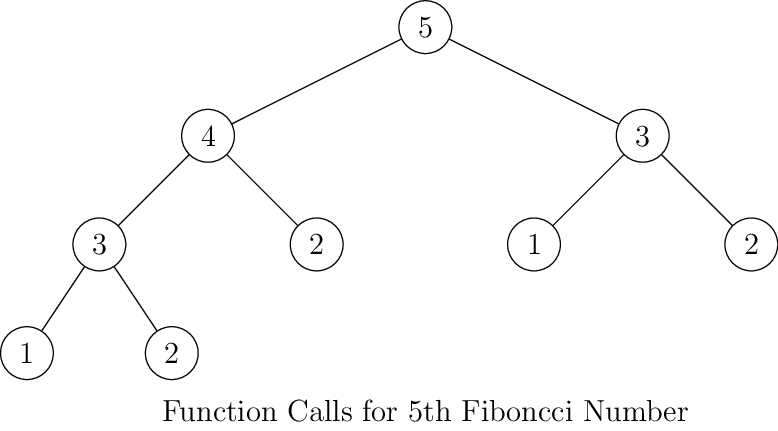
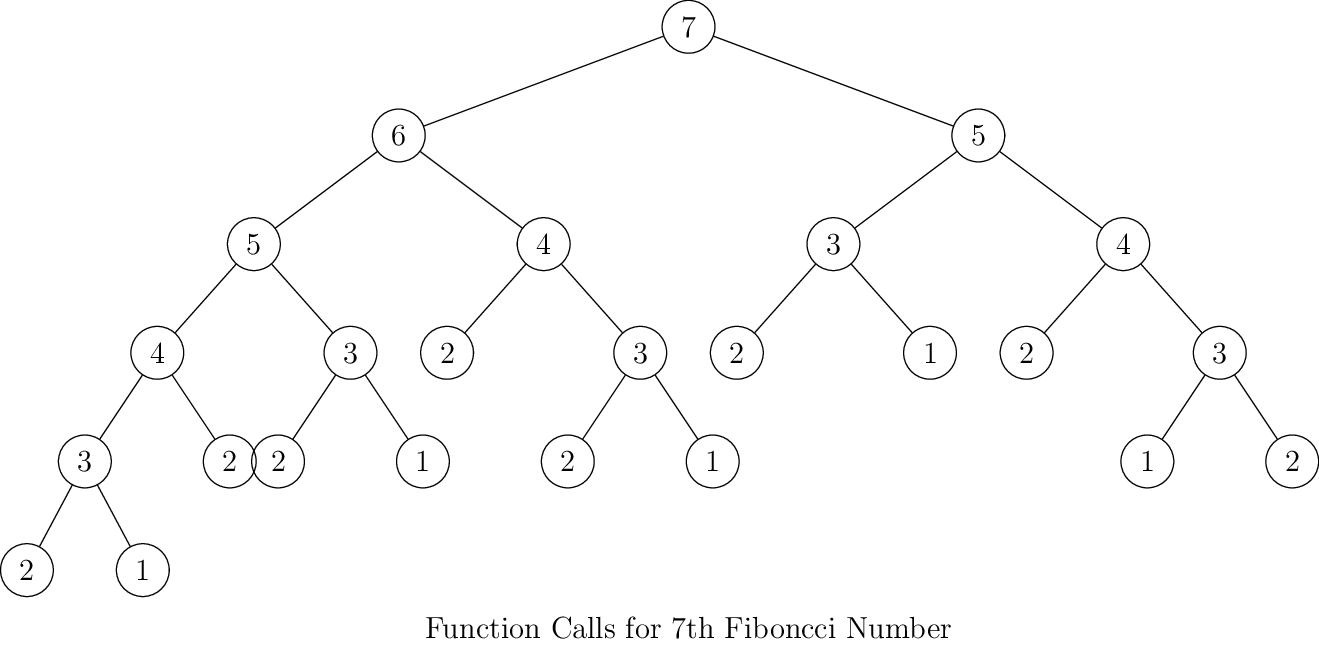
As you can see for every next number the number of elements on left and right side of the tree will be almost doubled. Thus, by intuition we can say that its complexity is \(O(2^n)\). However, that is not a tight bound. The tighter bound is given by \(O(\phi^n)\) where \(\phi\) is golden ratio i.e. \(\frac{1 + \sqrt{5}}{2}\). Computing tighter bound is very easy although it require little bit of mathematics which is not difficult at all. Fibonacci sequence can be written as two dimensional matrix of linear difference equations:
which gives,
solving for nth Fibonacci number we get,
2.3.2.1. Tail Recursive Version#
Thus, we see that complexity of computation of Fibonacci numbers is as given above. I would love to talk more about mathematical poperties of Fibonacci numbers in more details but I will leave that for mathematical part. Let us continue with recursion and efficiency of the above algorithm. We have seen that the tree form complexity will have very bad effect on runtime of the program. The simplification of multiple recursion form of Fibonacci sequence to single recursion form will allow us to do tail recursion. The code is given below:
#include <stdio.h>
void fib(unsigned int *input, unsigned long long *fib1, unsigned long long *fib2, unsigned long long *fibn)
{
if(*input == 0) {
return;
} else if(*input == 1) {
*fibn = 1;
return;
} else if(*input == 2) {
*fibn = 1;
return;
} else if (*input == 3){
*fibn = *fib1 + *fib2;
*fib1 = *fib2;
*fib2 = *fibn;
return;
} else {
*fibn = *fib1 + *fib2;
*fib1 = *fib2;
*fib2 = *fibn;
}
(*input)--;
fib(input, fib1, fib2, fibn);
}
int main()
{
unsigned int input = 0;
unsigned long long fib1 = 1;
unsigned long long fib2 = 1;
unsigned long long fibn = 0;
printf("Enter the fibonacci number you want(positive integer please):\n");
scanf("%u", &input);
fib(&input, &fib1, &fib2, &fibn);
printf("%llu is the Fibonacci number\n", fibn);
}
The implementation is slighly convoluted because of usage of pointers but it is still simple enough.
If you want to see if the code is really performing well then given below is output timed for 45th Fibonacci number. The version which took more time is the naive version.
computer:~ shivdayal$ time ./a.out
Which Fibonacci number you want?
45
1134903170
real 0m7.535s
user 0m6.796s
sys 0m0.008s
computer:~ shivdayal$ time ./a.out
Enter the fibonacci number you want(positive integer please):
45
1134903170 is the Fibonacci number
real 0m0.864s
user 0m0.001s
sys 0m0.002s
If I try to compute 50th number then it breaks my patience. But the tail recursive version blows away even the 80th number easily. As you will learn or would have noticed early such is power of tail recursion or better algorithms. Implementation does matter which you will see in next algorithm.
One more point I would here like to make is compilers are pretty good at optimization. For example, if we apply -O2 switch to the naive version of Fibnacci program then we see some improvement:
Which Fibonacci number you want?
45
1134903170
real 0m3.841s
user 0m2.640s
sys 0m0.003s
but it still is no match for our optimized tail recursive version. Thus, we can conslude that even through compilers are very smart we have to give them smart code as well. Compiler optimizes code and it can optimize better implementations even better.
2.3.3. Ackermann’s Function#
By the way, Ackermann was also David Hilbert’s(who is famous for Hilbert’s ten prolems) student for those who care. More of this will follow in mathematics part. Ackermann’s function is a very nasty function because even for small value of input it grows very fast. C does not have that kind of data type which can represent the values even for small inputs. It is a very good benchmark for the systems which can optimize recursion. To see how it grows so fast let us see how it expands:
2.3.3.1. Naive Implementation#
#include <stdio.h>
int ackermann(int m, int n)
{
if (!m) return n + 1;
if (!n) return ackermann(m - 1, 1);
return ackermann(m - 1, ackermann(m, n - 1));
}
int main()
{
int m, n;
for (m = 0; m <= 4; m++)
for (n = 0; n < 6 - m; n++)
printf("A(%d, %d) = %d\n", m, n, ackermann(m, n));
return 0;
}
and the output is:
A(0, 0) = 1
A(0, 1) = 2
A(0, 2) = 3
A(0, 3) = 4
A(0, 4) = 5
A(0, 5) = 6
A(1, 0) = 2
A(1, 1) = 3
A(1, 2) = 4
A(1, 3) = 5
A(1, 4) = 6
A(2, 0) = 3
A(2, 1) = 5
A(2, 2) = 7
A(2, 3) = 9
A(3, 0) = 5
A(3, 1) = 13
A(3, 2) = 29
A(4, 0) = 13
A(4, 1) = 65533
gcc does quite good optimization. For example, if I time the above code without optimization then I get following:
$ time ./a.out
A(0, 0) = 1
A(0, 1) = 2
A(0, 2) = 3
A(0, 3) = 4
A(0, 4) = 5
A(0, 5) = 6
A(1, 0) = 2
A(1, 1) = 3
A(1, 2) = 4
A(1, 3) = 5
A(1, 4) = 6
A(2, 0) = 3
A(2, 1) = 5
A(2, 2) = 7
A(2, 3) = 9
A(3, 0) = 5
A(3, 1) = 13
A(3, 2) = 29
A(4, 0) = 13
A(4, 1) = 65533
real 0m18.102s
user 0m18.080s
sys 0m0.018s
But if I compile it using -O3 flag then for the same code I have following:
$ time ./a.out
A(0, 0) = 1
A(0, 1) = 2
A(0, 2) = 3
A(0, 3) = 4
A(0, 4) = 5
A(0, 5) = 6
A(1, 0) = 2
A(1, 1) = 3
A(1, 2) = 4
A(1, 3) = 5
A(1, 4) = 6
A(2, 0) = 3
A(2, 1) = 5
A(2, 2) = 7
A(2, 3) = 9
A(3, 0) = 5
A(3, 1) = 13
A(3, 2) = 29
A(4, 0) = 13
A(4, 1) = 65533
real 0m1.748s
user 0m1.742s
sys 0m0.005s
The problem with converting Ackermann function to tail recursive version is storing the values of intermediate values of m for which we need data structure like a linked list. Although, an array can be used as well. However, to really show the complexity of Ackermann function you need data types much bigger than unsigned long long.
Another version of Ackermann function which is a tail-recursive version.
#include <stdio.h>
int ackermann(unsigned int *m, unsigned int *n, unsigned int* a, int* len)
{
if(!*m && *len == -1) {
return ++*n;
}
else if(!*m && *len >= 0) {
++*n;
*m = a[(*len)--];
}
else if(*n == 0) {
--*m;
*n = 1;
} else {
++*len;
a[*len] = *m - 1;
--*n;
}
return ackermann(m, n, a, len);
}
int main()
{
unsigned int m=4, n=1;
unsigned int a[66000];
int len = -1;
for (m = 0; m <= 4; m++)
for (n = 0; n < 6 - m; n++) {
unsigned int i = m;
unsigned int j = n;
printf("A(%d, %d) = %d\n", m, n, ackermann(&i, &j, a, &len));
}
return 0;
}
But we have not improved the complexity of the algorithm. i.e. our computation effort has not decreased thus even with optimization it performs worse than our naive version. The timings are given below:
$ time ./a.out
A(0, 0) = 1
A(0, 1) = 2
A(0, 2) = 3
A(0, 3) = 4
A(0, 4) = 5
A(0, 5) = 6
A(1, 0) = 2
A(1, 1) = 3
A(1, 2) = 4
A(1, 3) = 5
A(1, 4) = 6
A(2, 0) = 3
A(2, 1) = 5
A(2, 2) = 7
A(2, 3) = 9
A(3, 0) = 5
A(3, 1) = 13
A(3, 2) = 29
A(4, 0) = 13
A(4, 1) = 65533
real 0m2.934s
user 0m2.926s
sys 0m0.006s
However, we can improve this by doing caching previous results which is shown in the following piece of code:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int m_bits, n_bits;
int *cache;
int ackermann(int m, int n)
{
int idx, res;
if (!m) return n + 1;
if (n >= 1<<n_bits) {
printf("%d, %d\n", m, n);
idx = 0;
} else {
idx = (m << n_bits) + n;
if (cache[idx]) return cache[idx];
}
if (!n) res = ackermann(m - 1, 1);
else res = ackermann(m - 1, ackermann(m, n - 1));
if (idx) cache[idx] = res;
return res;
}
int main()
{
int m, n;
m_bits = 3;
n_bits = 20; /* can save n values up to 2**20 - 1, that's 1 meg */
cache = malloc(sizeof(int) * (1 << (m_bits + n_bits)));
memset(cache, 0, sizeof(int) * (1 << (m_bits + n_bits)));
for (m = 0; m <= 4; m++)
for (n = 0; n < 6 - m; n++)
printf("A(%d, %d) = %d\n", m, n, ackermann(m, n));
return 0;
}
and the timing is given below:
$ time ./a.out
A(0, 0) = 1
A(0, 1) = 2
A(0, 2) = 3
A(0, 3) = 4
A(0, 4) = 5
A(0, 5) = 6
A(1, 0) = 2
A(1, 1) = 3
A(1, 2) = 4
A(1, 3) = 5
A(1, 4) = 6
A(2, 0) = 3
A(2, 1) = 5
A(2, 2) = 7
A(2, 3) = 9
A(3, 0) = 5
A(3, 1) = 13
A(3, 2) = 29
A(4, 0) = 13
A(4, 1) = 65533
real 0m0.005s
user 0m0.002s
sys 0m0.002s
2.4. Binary Search#
Searching a set of data is one of the most common and important operations in computer science. The importance of the search can be recognized from the success Google. The problem with search is that it is easy to search small amount of data but harder for large set. Most of the time we search for strings and rarely for numbers. The simplest approach would be the naive, brute force method to compare each item of the collection with the key to be searched which would result in \(O(n)\) time complexity, which simply is not good enough. Another problem is that since we compare strings that would result in increased time complexity other than that is for search. The first improvement which we can do on linear search is by using binary search algorithm. Binary search is a classic divide and conquer algorithm which tells if a value is present in a set of values in log_2(n). The prerequisite of applying binary search is that input set is sorted.
In binary search we find the mid element of our set. Let us say that our set or array is sorted in increasing order. If key is equal to the value of mid element we want to search then we return the value. If key is less than value of mid element then we consider the left half of array repeat the process. If key is greater than value of mid element then we consider the right half of array and repeat the process. Once we exhaust the resulting array to last one value by repeatedly dividing in half and still we have not found the value then the key is not found.
First let us see an iterative version of the algorithm:
#include <stdio.h>
#include <stddef.h>
int main()
{
size_t first, last, middle, search;
size_t array[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8 ,9};
printf("Enter value to find\n");
scanf("%zu", &search);
first = 0;
last = 9;
middle = (first+last)/2;
while (first <= last) {
if (array[middle] < search)
first = middle + 1;
else if (array[middle] == search) {
printf("%zu found at location %zu.\n", search, middle);
break;
}
else
last = middle - 1;
middle = (first + last)/2;
}
if (first > last)
printf("Not found! %zu is not present in the list.\n", search);
return 0;
}
Now let us see recursive version:
#include <stdio.h>
#include <stddef.h>
void binary_search(size_t *a, size_t first, size_t last, size_t search)
{
size_t middle = (first+last)/2;
if (first > last) {
printf("Not found! %zu is not present in the list.\n", search);
return;
} else {
if (a[middle] < search)
first = middle + 1;
else if (a[middle] == search) {
printf("%zu found at location %zu.\n", search, middle);
return;
}
else
last = middle - 1;
}
binary_search(a, first, last, search);
}
int main()
{
size_t first, last, search;
size_t a[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8 ,9};
printf("Enter value to find\n");
scanf("%zu", &search);
first = 0;
last = 9;
binary_search(a, first, last, search);
return 0;
}
While you may think that this solution is correct the truth cannot be farther from it. There is a gaping issue with the code presented above. Read the code again and see if you can find that. For the time being I will entertain you with a quote from Donald E. Knuth.
On the funnier side of life it is not that only novice programmers make mistakes. Even expert programmers make mistakes. John Bentley, author of very good books(Programming Pearls, More Programming Pearls and Writing Efficient Programs) assigned it as a problem in a course for professional programmers. Surprisingly, ninety percent could not write correct code even after several hours. Even his own implementation in 1986 print of Programming Pearls, contained an error which remained there for 20 years.
Coming back to the error, it is on the line which contains the code middle = (first + last)/2;. Experienced programmer would have already noticed it. The problem is common when you add any two numbers there is always a chance that sum will overflow. Thus, you need to cast it to larger data type. Since, we are using size_t for data type which is good enough for holding average of two such numbers we do not need to cast it. If it would have been just plain sum then we would have needed long long or its unsigned counterpart to be accurate. Here, we can use a nifty calculation to find out the average. We can write the same calculation as middle = last + (first - last)/2;, which would work for all values of first and last.
2.5. A Simple Problem of Average Calculation#
Although it is not related to recursion, following the above discussion on overflow a simple problem can be formulated. Given an array of numbers find out its average. Now this is very simple and beginners always cause overflow in this. Floating-point division is allowed for the sake of accuracy. The above logic can be easily extended. For example, average of n numbers is given by
\(average = \frac{a_0 + a_1 + \ldots + a_n}{n}\)
which can be rewritten as:
\(average = a_0 + \frac{a_1 - a_0 + a_2 - a_0 + \ldots + a_n - a_0}{n}\)
Implementing the above formula will cause no overflow. An example implementation is given below:
#include <stdio.h>
#include <stddef.h>
int main()
{
size_t n = 0;
printf("Enter the size of array:\n");
scanf("%zu", &n);
int a[n];
printf("Enter the elements of the array:\n");
for(size_t i = 0; i < n; ++i)
scanf("%d", &a[i]);
double average = a[0];
for(size_t i = 1; i < n; ++i)
{
average += (a[i]-a[0])/(float)n;
}
printf("Average is %lf\n", average);
return 0;
}
Again, coming back to the binary search implementation you would notice that if there are duplicates in the array then the position of key can be anything. The above implementation do not guarantee that lowest index of duplicate search elements will be returned. For example, consider following case:
#include <stdio.h>
#include <stddef.h>
void binary_search(size_t *a, size_t first, size_t last, size_t search)
{
size_t middle = (first+last)/2;
if (first > last) {
printf("Not found! %zu is not present in the list.\n", search);
return;
} else {
if (a[middle] < search)
first = middle + 1;
else if (a[middle] == search) {
printf("%zu found at location %zu.\n", search, middle);
return;
}
else
last = middle - 1;
}
binary_search(a, first, last, search);
}
int main()
{
size_t first, last, search;
size_t a[10] = {0, 1, 2, 3, 4, 8, 8, 8, 8 ,9};
printf("Enter value to find\n");
scanf("%zu", &search);
first = 0;
last = 9;
binary_search(a, first, last, search);
return 0;
}
The value \(8\) will always be found at \(6th\) index. The loss is that this algorithm makes early termination impossible. For large arrays that are a power of \(2\), the savings is about two iterations. Half the time, a match is found with one iteration left to go; one quarter the time with two iterations left, one eighth with three iterations, and so forth. The infinite series sum is \(2\).
The calculation of infinite series is given below:
\(S = \frac{1}{2} + \frac{2}{4} + \frac{3}{8} + \frac{4}{16} + \frac{5}{32} + \ldots\)
\(\frac{S}{2} = \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{4}{32} + \ldots\)
Subtracting and solving geometric series we get sum as \(2\).
2.5.1. Complexity Analysis of Binary Search#
The worst case and average case complexity of binary search is \(O(\log_2(n))\) while the best case is \(O(1)\). Space complexity of binary search is \(O(1)\) because no extra space is needed. Computation of time complexity is really easy. Say, we begin with array of size n then clearly we will divide the array in half and in worst case our smallest array would be of size \(1\). Let us say that take \(k\) steps then clearly \(n=2^k\), i.e. \(k=\log_2(n)\). Thus, in those many \(k\) i.e. \(k=\lfloor\log_2n\rfloor\) to round \(k\) to next integral value.
2.6. Towers of Hanoi(Brahma)#
The next example is the famous Towers of Hanoi which is also known as Towers of Brahma or Lucas’ Tower. This puzzle was invented by the French Mathematician Edouard Lucas in \(1883\). There is a story about an Indian temple in Kashi Vishwanath which contains a large room with three time-worn posts in it surrounded by \(64\) golden disks. According to directive issued by Hindu God Brahma the Brahmin priests are moving the disks. According to the directive of Brahma once priest would have moved all the disks then the world will end.
If the legend were true, and priests moved the disks in such way that it would require minimum no. of moves and they take one second per disk movement, it would take them \(2^{64}-1\) seconds or roughly \(585\) billion years, or \(18,446,744,073,709,551,615\) turns to finish, or about \(127\) times the current age of the sun. Thus, there is no need to worry because earth will not have a source of energy, which supports all the life. The other variation of the legend replaces priests with monks, temple with monastery and location with Hanoi, Vietnam. For us, the programmers, the location does not matter neither does the legend. What matters is a program which can solve this puzzle. First let us have a pictorial representation of the problem then we will observe the constraints imposed on us by Gods about the puzzle.
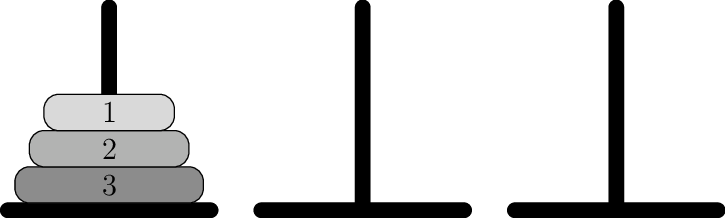
The objective of the puzzle is to move all disks from leftmost stand to rightmost under following rules:
Only one disk must be moved at a time.
A move can only take the uppermost disk from one of the towers and place it on top of another tower.
No disk may be placed on top of a smaller disk.
First we do a recursive solution and then we will see the iterative solution as iterative one is trickier. Consider a stack of \(n\) disks. Then, we consider it as two disks. One consists of \(n-1\) disks and the nth disk. Then, we move them to appropriate pegs and then we split \(n-1\) disks in two i.e. one of \(n-2\) and then another of \(n-1\). Thus, recursive solution is implemented. Given below is the recursive version of the code:
#include <stdio.h>
void move(int n, char left, char right, char mid)
{
if(n > 0) {
// move n-1 disks from left to mid
move(n-1, left, mid, right);
// move nth disk from left to right
printf("Moved disk %d from left to right\n", n);
// move n-1 disks from mid to right
move(n-1, mid, left, right);
}
}
int main()
{
unsigned int n = 0;
printf("How many disks you want to move?\n");
scanf("%d", &n);
move(n, 'L', 'R', 'C'); // L is left, R is right and C is center disk
return 0;
}
and the output is:
How many disks you want to move?
3
Moved disk 1 from left to right
Moved disk 2 from left to right
Moved disk 1 from left to right
Moved disk 3 from left to right
Moved disk 1 from left to right
Moved disk 2 from left to right
Moved disk 1 from left to right
From the description of the program it appears hard to understand but the program is really simple if you look at the output for \(2, 3, 4\) and \(5\) disks one by one. Once you see how stack is winded and unwinded then you will understand the solution. The description says move \(n-1\) disks but in reality there is no such movement of \(n-1\) disks but that is propagated further to next function. In reality, you move \(1\) disk. The description is abstract and conceptual just to describe the solution.
The iterative solution is not very intuitive to figure easily thus I will present it straight away. Optimal solution is divided in two cases; one for odd and another for even no. of disks.
If even no. of disks are in question:
move disk between left to center
move disk between left to right
move disk between center and right
If odd no. of disks are in question:
move disks between left and right
move disks between left and center
move disks between center and right
rinse and repeat till complete
An iterative implementation is given below:
#include <stdio.h>
#include <stdlib.h> // for malloc
#include <limits.h> // for UINT_MIN
#include <math.h> // for calculating total no. of moves
// we create a stack of disks
typedef struct stack {
// used for creating stack
int capacity;
// top of stack
int top;
// contiguous array to hold disks
int* array;
}stackT;
stackT* create_stack( int capacity)
{
stackT* s = (stackT*)malloc(sizeof(stackT));
s->capacity = capacity;
s->top = -1;
s->array = ( int*)malloc(sizeof(int)*s->capacity);
return s;
}
// obviously stack is full when top is the last element
int is_full(stackT* s)
{
return (s->top == s->capacity - 1);
}
// same as full stack is empty if top is -1
int is_empty(stackT* s)
{
return (s->top == -1);
}
// push an element to stack increasing top
void push(stackT* s, int element)
{
if (is_full(s))
return;
s->array[++s->top] = element;
}
// pop an element from stack
int pop(stackT* s)
{
if (is_empty(s))
return INT_MIN;
return s->array[s->top--];
}
void move_disks(stackT* left, stackT* right, char l, char r)
{
int l_disk = pop(left);
int r_disk = pop(right);
// When l is empty
if (l_disk == INT_MIN)
{
push(left, r_disk);
printf("Move the disk %d from \'%c\' to \'%c\'\n", r_disk, r, l);
}
// When r is empty
else if (r_disk == INT_MIN)
{
push(right, l_disk);
printf("Move the disk %d from \'%c\' to \'%c\'\n", l_disk, l, r);
}
// When top disk of l > top disk of r
else if (l_disk > r_disk)
{
push(left, l_disk);
push(left, r_disk);
printf("Move the disk %d from \'%c\' to \'%c\'\n", r_disk, r, l);
}
// When top disk of l < top disk of r
else
{
push(right, r_disk);
push(right, l_disk);
printf("Move the disk %d from \'%c\' to \'%c\'\n", l_disk, l, r);
}
}
// implement core logic
void hanoi_iter( int n, stackT* left, stackT* mid, stackT* right)
{
long i, total_moves;
char l = 'L', r = 'R', m = 'M';
// if no. of disks is even then we need to swap M and R
if(n % 2 == 0) {
char temp = r;
r = m;
m = temp;
}
total_moves = pow(2, n) - 1;
// obviously larger no. represent larger disks to they will
// be pushed first
for(i = n; i >= 1; i--) {
push(left, i);
}
for(i = 1; i <= total_moves; ++i) {
if(i % 3 == 1) {
move_disks(left, right, l, r);
} else if (i % 3 == 2) {
move_disks(left, mid, l, m);
} else if (i % 3 == 0) {
move_disks(mid, right, m, r);
}
}
}
int main()
{
int n = 0;
printf("How many disks you want?\n");
scanf("%d", &n);
stackT *left, *mid, *right;
// Create three stacks of size 'n'
// to hold the disks
left = create_stack(n);
mid = create_stack(n);
right = create_stack(n);
hanoi_iter(n, left, mid, right);
return 0;
}
and the output is:
How many disks you want?
3
Move the disk 1 from 'L' to 'R'
Move the disk 2 from 'L' to 'M'
Move the disk 1 from 'R' to 'M'
Move the disk 3 from 'L' to 'R'
Move the disk 1 from 'M' to 'L'
Move the disk 2 from 'M' to 'R'
Move the disk 1 from 'L' to 'R'
2.6.1. Time and Space Complexity#
Let the time required for \(n\) disks is \(T(n)\). As you can see, there are \(2\) recursive calls for \(n-1\) disks and one constant time operation to move a disk from ‘left’ peg to ‘right’ peg. Let the cost of this constant time operation be \(k1\).
Therefore,
\(T(n)=2T(n-1)+k_1\)
\(T(0)=k_2\), a constant.
\(T(1)=2k_2+k1\)
\(T(2)=4k_2+2k_1+k1\)
\(T(2)=8k_2+4k_1+2k_1+k1\)
Coefficient of \(k_1=2^n\). Coefficient of \(k_2=2^{n-1}\). Therefore, time complexity is \(O(2^n)\).
Thus, you see in closed for of time complexity is exponential and it double for every extra disk. Exponentially complex algorithms are very expensive in nature and if you believe in mythology then universe is going to stay for a long long time so do not fret.
For both the versions storage is required only for disks i.e. a unit constant space. So for \(n\) disks space complexity is \(O(n)\), which is linear and quite good because space complexity is rarely less than linear because you never want to lose original data. Only in extreme cases algorithms allow destruction of original data in that case space complexity is less than what we have observed for this problem.