4. Linked List Solutions#

and 2. will be implemented in next chapter.

You can add these two lines to linked list implementation as prototype for implementation for iterative and recursive version.
```
void reverse(ll**);
void rreverse(ll**, ll*);
```
The most important thing is to be able to think how we are going to do the implementation. Let us first take the case of non-recursive part. We can visualize the linked list as nodes attached with pointers. So all we have to do is make head point to the last node. We reverse the pointer. Now since the pointer is broken we need to maintain two pointers the current node and the next node, hence, we will need two extra pointers. Now as next pointer is broken we can keep assigning current pointer to it as shown in the diagram below:

The equivalent code for the above can be written as:
```
void reverse(ll** head)
{
    ll *next = NULL;
    ll *current = NULL;

    if(!(*head))
        return;

    while((*head)->next != NULL)
    {
        next = (*head)->next;
        (*head)->next = current;
        current = *head;
        (*head) = next;
    }
    (*head)->next = current;
}
```
Notice that when we reach the end of node the pointer next will be in broken state and therefore from last pointer whose next would be pointing NULL must be made to point to current node as shown. The entire process is shown in the diagram below(we start with a list having three nodes 10, 20 and 30. Again see the image form bottom to top.):

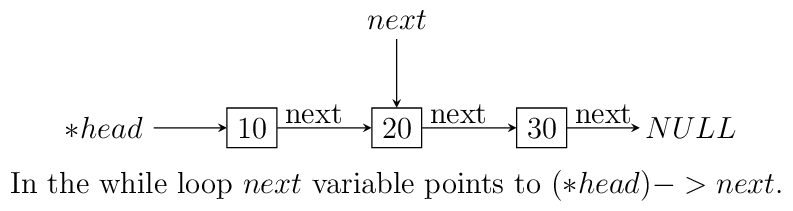
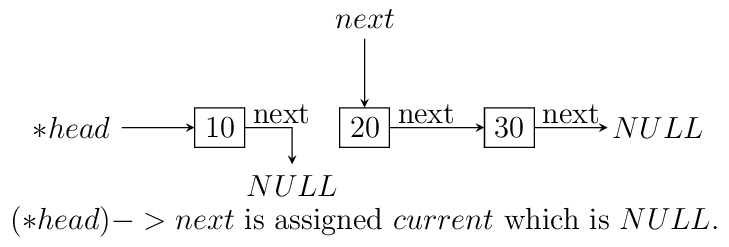
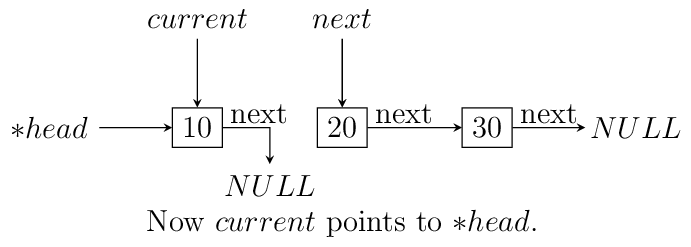
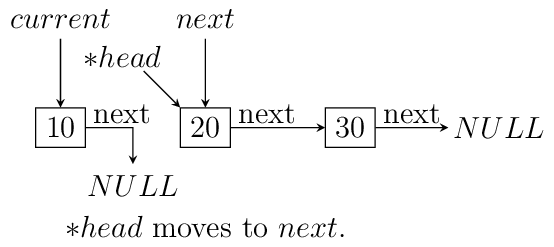
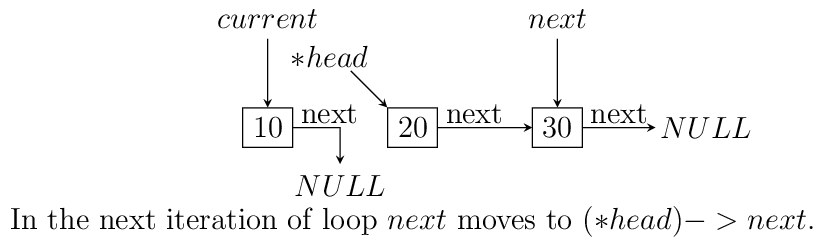
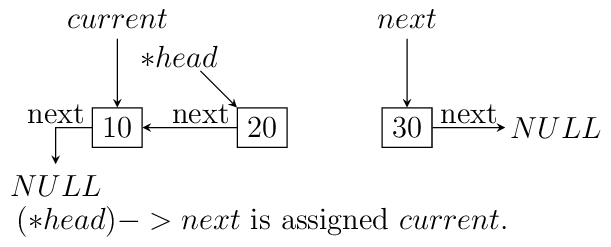
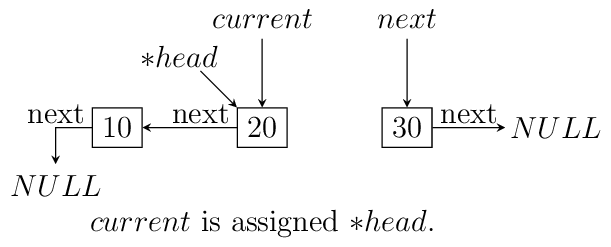
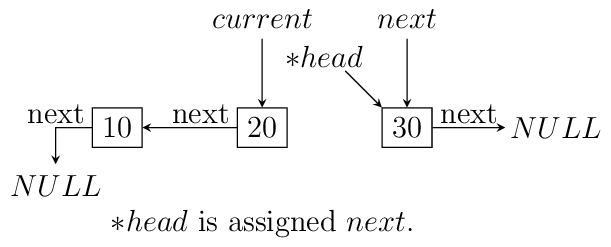
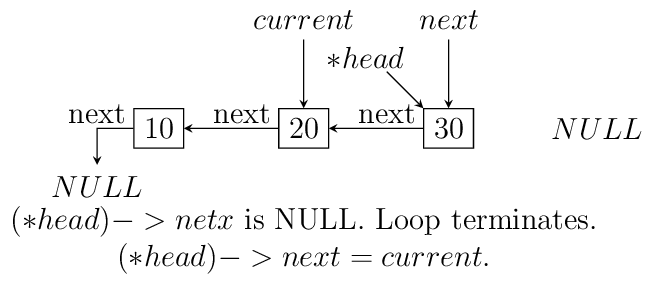
Iterative reversal of a singly linked list.

For recursive version first we need a condition to iterate to last node. Then if next of next is not NULL then we make that point to currrent node. The current node’s next is useless for us and we make it NULL because the first node which will be last after reversal will have next pointing to NULL which is good for us. Now if next is NULL then we are at last node and let us make this head. The entire operation can be visualized below:

The code which does recursive iteration is given below:
```
void rreverse(ll** head, ll* current)
{

    if(!(*head))
        return;

    if(current->next != NULL)
    {
        rreverse(head, current->next);
    }

    if(current->next != NULL)
    {
        current->next->next = current;
        current->next = NULL;
    }
    else
        *head=current;
}
```
The call to rreverse must ensure that current is sent with the same value as head. Also, remember to update the menu and switch cases. As you can see if your linked list with less than two elements then code will not change anything. Let us see what happens if we call this function rreverse like rreverse(&head, head);. For this example consider a list having four elements 10, 20 30 and 40.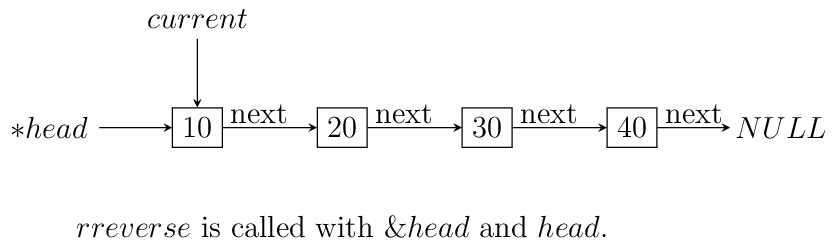

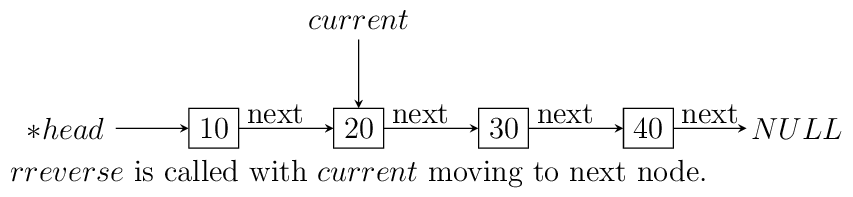
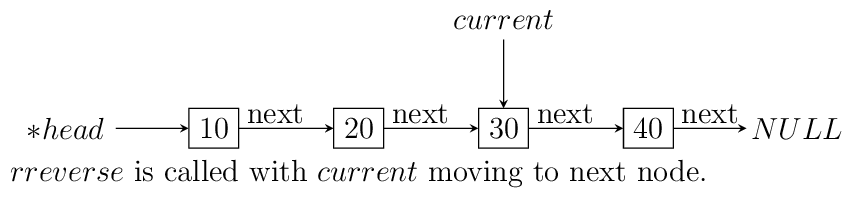
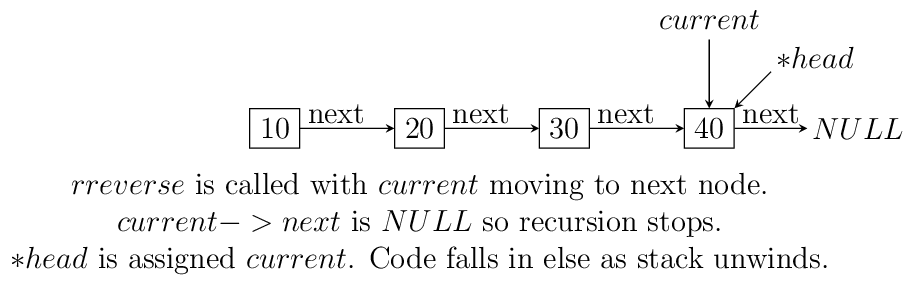
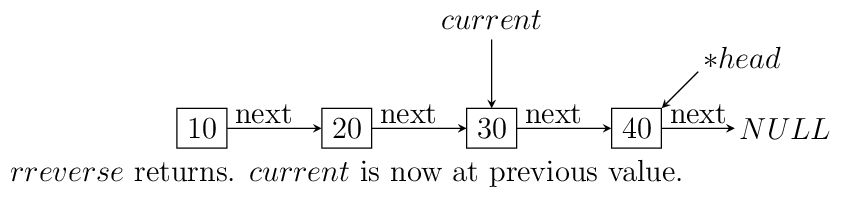
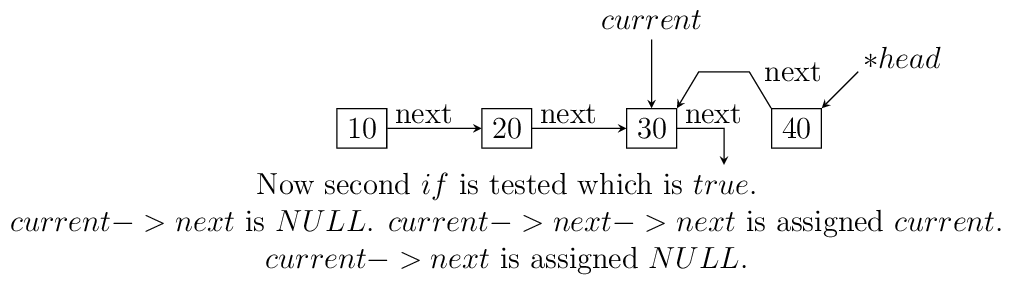
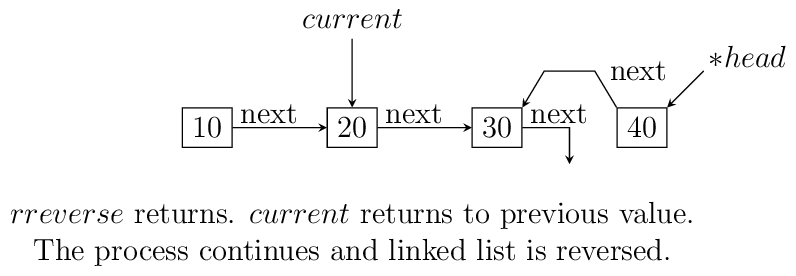
Resursive reversal of a singly linked list.
This will be done after bubble sort is discussed.
This will be done after quick sort is discussed.
This will be done after merge sort is discussed.
There are several ways of doing this.
1. You can use a hash table(we have not discussed hashing yet) to store the address of each node. If NULL is reached then you know that there is no loop. However, if insertion in hash table fails because that address is already present then you know that there is a loop. This would require \(O(n)\) extra space.
2. The second method is rather crude and that requires modification to linked list structure. You can put a boolean flag which will mark if a node is visited. If a node is visited and you are revisiting again in traversal then there is a loop. Using boolean has a flaw that you can mark it only once and subsequently you cannot determine if the list has a loop. This can be overcome by making the boolean flag an unsigned integer which can support a large no. of iterations over the list. You can use boolean also and use it repeatedly if you make sure that you reset all the values if no loop is found. That would be another overhead of \(O(n)\) in terms of time complexity and storage requirement is also increasing by \(O(n)\).
3. There are two popular algorithms for cycle detection in any sequence. First is Floyd’s algorithm and second is Brent’s algorithm. We will study these two in their full glory later. For now, we will concentrate on Floyd’s algorithm in context of finding loop in a linked list. We will not concern ourselves with rigorous mathematical proof of this method.
  
  Floyd’s algorithm is based on a simple technique that we need two iterators(read pointers) over our set(linked list). One moves two elements while the other moves one element at a time and eventually they will meet i.e. pointers will become equal and that will prove that our set(linked list) has a loop. The implementation is very simple and in context with our linked list it is implemented as a function which you can execute in conjunction to find if there is a loop in question.
```
int floyd_detect_loop_algorithm(ll *head)
{
  ll *slow = head, *fast = head;

  while(slow && fast && fast->next )
  {
    slow = slow->next;
    fast  = fast->next->next;
    if (slow == fast)
    {
      printf("Loop detected.\n");
      return 1;
    }
  }

  return 0;
}
```
  Let us say \(\lambda\) is the length of loop and \(\mu\) is the index of first element where loop starts then the time complexity of this algorithm is \(O(\lambda + \mu)\) and as you can see we need storage only for two pointers the space complexity would be \(\Theta(1)\).