27. Height and Distance#

There are problems where distances between two points are not directly measurable or difficult. Most of such problems can be solved by applying trigonometric ratios with ease. This chapter is dependent on application of what we have studied so far about trigonometric ratios.

Angle of Elevation:

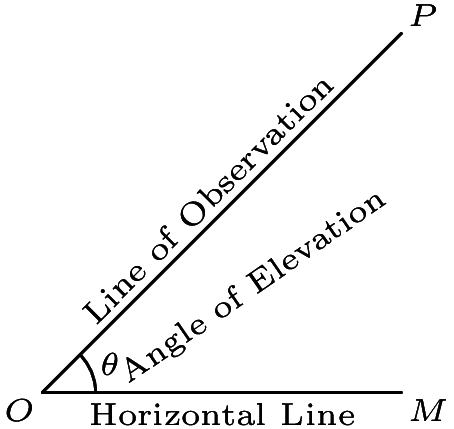
Let $O$ and $P$ be two points, where $P$ is at a higher level than $O$ . Also let $O$ be the position of observer and $P$ the position of the object. Draw a horizontal line $OM$ through the point $O$ . $OP$ is called the line of observation or line of sight. Then $\angle POM = \theta$ is called the angle of elevation of $P$ as observed from $O$ .
Angle of Depression

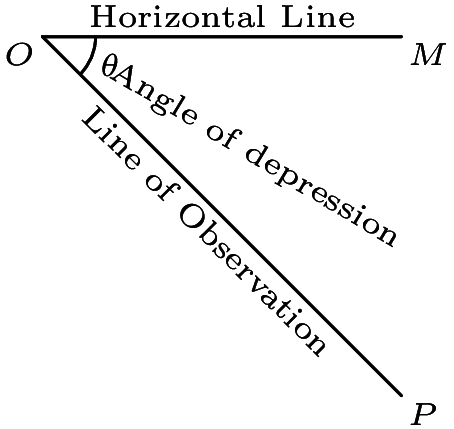
In the above example, if $P$ be at a lower level than $O$ , then $\angle MOP = \theta$ is called the angle of depression.
Bearing

In the above example, if the observer and the object i.e. $O$ and $P$ be on the same level then bearing is defined. Four standard directions; East, West, North and South are taken as cardinal directions for measuring bearing. If $\angle POE = \theta$ is the bearing of point $P$ with respect to $O$ measured from East to North.

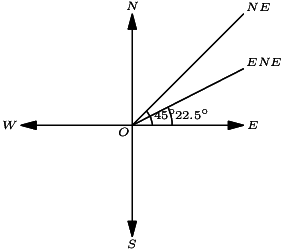
North-east means equally inclines to north and east. South-east means equally inclines to south and east. E-N-E means equally inclined to east and north-east.

Solutions of the problems in this chapter depends on what we have studied so far. Thus, it is very important that you have studied previous chapters and understood the concepts fully.

27.1. Some Useful Properties of a Circle#

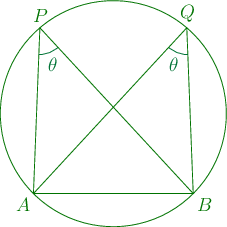
Angles on the same segment of a circle are equal. Alternatively, we can say that if the angles $APB$ and $AQB$ subtended on the segment $AB$ are equal, a circle will pass through the points $A, B, P$ and $Q$ i.e. these points are concyclic.
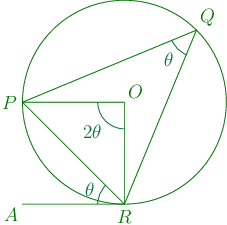
If $AR$ be the tangent to the circle passing through $P, Q$ and $R$ then $\angle PRA = \angle PQR = \theta$

Also, if $PQ$ subtends greatest angle at $R$ which lies on the line $AR$ , then point $R$ will be the point of contact of the tangent to the circle passing through $P, Q$ and $R$ .

27.2. Problems#

A tower is $100\sqrt{3}$ meters high. Find the angle of elevation of its top point from a point $100$ meters away from its foot.
The angle of elevation of the top of a tower from a point on the ground, which is $30$ m away from the foot of the tower is $30^\circ$ . Find the height of the tower.
A kite is flying at a height of $60$ m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is $60^\circ$ . Find the length of the string assuming there is no slack in the string.
The string of a kite is $100$ m long and it makes an angle of $60^\circ$ with the horizontal. Find the height of the kite, assuming there is no slack in the string.
A circus artist is climbing from the ground a rope stretched from the top of a vertical pole and tied to the ground. The height of the pole is $12$ m and the angle made by the rope with the ground level is $30^\circ$ . Calculate the distance covered by the artist in climbing to the top of the pole.
A circus artist is climbing a $20$ m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is $30^\circ$ .
A bridge across a river makes an angle of $45^\circ$ with the river banks. If the length of the bridge across the river is $150$ m, what is the width of the river?
An observer $1.5$ m tall is $28.5$ m away from a tower. The angle of elevation of the top of the tower from her eyes is $45^\circ$ . What is the height of the tower?
An electician has to repair an electric fault on a pole of a height $4$ m. He needs to reach a point $1.3$ m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use when inclined at an angle of $60^\circ$ to the horizontal would enable him to reach the required position?
From a point on the ground $40$ m away from the foot of the tower, the angle of elevation of the top of the tower is $30^\circ$ . The angle of elevation of the top of a water tank(on the top of the tower) is $45^\circ$ . Find (i) height of the tower (ii) the depth of the tank.
A person, standing on the bank of a river, observes that the angle subtended by a tree on the opposite bank is $60^\circ$ . When he retreats $20$ m from the bank, he finds the angle to be $30^\circ$ . Find the height of the tree and the breadth of the river.
A tree $12$ m high, is broken by the wind in such a way that its top touches the ground and makes an angle of $60^\circ$ with the ground. At what height from the bottom the tree is broken by the wind?
A tree is broken by the wind. The top struck the ground at an angle of $30^\circ$ and at a distance of $30$ m from the root. Find the whole height of the tree.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent in $5/12$ . On walking $192$ m towards the tower, the tangent of the angle of elevation is $3/4$ . Find the height of the tower.
The shadow of a vertical tower on level ground increases by $10$ m, when the altitude of sun changes from an angle of elevation $45^\circ$ to $30^\circ$ . Find the height of the tower.
From the top of a hill, the angle of depression of two consecutive kilometer stones due east are found to be $30^\circ$ and $45^\circ$ . Find the height of the hill.
Determine the height of a mountain if the elevation of its top at an unknown distance from the base is $30^\circ$ and at a distance $10$ km further off from the mountain, along the same line, the angle of elevation is $15^\circ.$ (Use $\tan 15^\circ = 0.27$ ).
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is $60^\circ$ . When he moves $40$ m away from the bank, he finds the angle of elevation to be $30^\circ$ . Find the height of the tree and width of the river.
An aeroplane at an altitude of $1200$ m finds that two ships are sailing towards it in the same direction. The angles of depression of the ships as observed from the aeroplane are $60^\circ$ and $30^\circ$ respectively. Find the distance between two ships.
The shadow of a flag-staff is three times as long as the shadow of the flag-staff when the sun rays meet the ground at an angle of $60^\circ$ . Find the angle between the sun rays and the ground at the time of longer shadow.
An aeroplane at an altitude of $200$ m observes the angle of depression of opposite sign on the two banks of a river to be $45^\circ$ and $60^\circ$ . Find the width of the river.
Two pillars of equal height and on either side of a road, which is $100$ m wide. The anngle of elevation of the top of the pillars are $60^\circ$ and $30^\circ$ at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
As observed from the top of a lighthouse, $100$ m above sea level, the angle of depression of a ship, sailing directly towards it, changes from $30^\circ$ to $45^\circ$ . Determine the distance travelled by the ship during the period of observation.
The angle of elevation of the top $Q$ of a vertical tower $PQ$ from a point $X$ on the ground is $60^\circ$ . At a point $Y$ , $40$ m vertically above $X$ , the angle of elevation is $45^\circ$ . Find the height of the tower $PQ$ and the distance $XQ$ .
From a window $15$ m high above the ground in a street, the angles of elevation and depression of the top and the foot of another hourse on the opposite side of the street are $30^\circ$ and $45^\circ$ respectively show that the height of the opposite house is $23.66$ m. (Use $\sqrt{3} = 1.732$ ).
From the top of a building $60$ m high the angles of depression of the top and the bottom of tower are observed to be $30^\circ$ and $60^\circ$ . Find the height of the tower.
A man standing on the deck of a ship, which is $10$ m above the water level. He observes that the angle of elevation of the top of the hill as $60^\circ$ and the angle of depression of the base of the hill as $30^\circ$ . Calculate the distance of the hill from from the ship and the height of the hill. Given that level of water is in the same line with base of the hill.
The angle of elevation of a jet plane from a point $A$ on the ground in $60^\circ$ . After a flight of $30$ seconds the angle of elevation changes to $30^\circ$ . If the jet plane is flying at a constant height of $3600\sqrt{3}$ m, find the speed of the jet plane.
There is a small island in the middle of a $100$ m wide river and a tall tree stands on the island. $P$ and $Q$ are points directly opposite to each other on two banks in the line with the tree. If the angle of elevation of the top of the tree from $P$ and $Q$ are respectively $30^\circ$ and $45^\circ$ , find the height of the tree.
The horizonatal distance between two towers is $140$ m. The angle of elevation of the top of the first tower when seen from the second tower is $30^\circ$ . If the height of the second tower is $60$ m, find the height of the first tower.
An aeroplane when flying at a height of $4000$ m from the ground passes vertically above anohter aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are $60^\circ$ and $45^\circ$ respectively. Find the vertical distance between the aeroplanes at that instant.
A tower stands vertically on the ground. From a point on the ground, $20$ m away from the foot of the tower, the angle of elevation of the top of the tower is $60^\circ$ . What is the height of the tower?
The angle of elevation of a ladder leaning against a wall is $60^\circ$ and the foot of the ladder is $9.5$ m away from the wall. Find the length of the ladder.
A ladder is placed along the wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is $2$ m away from the wall and the ladder is making an angle of $60^\circ$ with the level of the ground. Determine the height of the wall.
An electric pole is $10$ m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of $45^\circ$ with the horizontal through the foot of the pole, find the length of the wire.
A kite is flying at a height of $75$ m from the ground level, attached to a string inclined at $60^\circ$ to the horizontal. Find the length of the string to the nearest meter.
A ladder $15$ m long just reaches the top of a vertical wall. If the ladder makes an angle of $60^\circ$ , find the height of the wall.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane $70$ m away from the tower, an observer notices that the angle of elevation of the top and the bottom of the flag-staff are $60^\circ$ and $45^\circ$ respectively. Find the height of the flag-staff and that of the tower.
A vertically straight tree, $15$ m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of $60^\circ$ with the ground. At what height from the ground did it break?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height $5$ m. At a point on the plane, the angle of elevation of the top and the bottom of the flag-staff are respectively $30^\circ$ and $60^\circ$ . Find the height of the tower.
A person observed the angle of elevation of the top of the tower as $30^\circ$ . He walked $50$ m towards the foot of the tower along the ground level and found the angle of elevation of the top of the tower to be $60^\circ$ . Find the height of the tower.
The shadow of the tower, when the angle of elevation of the sun is $45^\circ$ , is found to be $10$ m longer than when it was $60^\circ$ . Find the height of the tower.
A skydiver is descending vertically and makes angles of elevation of $45^\circ$ and $60^\circ$ at two observing points $100$ m apart from each other on the left side. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the nearest observation point.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are $45^\circ$ and $60^\circ$ . If the height of the tower is $150$ m, find the diistance between the objects.
The angle of elevation of a tower from a point on the same level as the foot of the tower is $30^\circ$ . On advancing $150$ m towards the foot of the tower, the angle of elevation of the tower becomes $60^\circ$ . Find the height of the tower.
The angle of elevation of the top of a tower as observed from a point in the horizontal plane through the foot of the tower is $30^\circ$ . When the observer moves towards the tower a distance of $100$ m, he finds that angle of elevation has become $60^\circ$ . Find the height of the tower and distance of the initial position from the tower.
From the top of a building $15$ m high the angle of elevation of the top of a tower is found to be $30^\circ$ . From the bottom of the same building, the angle of elevation of the same tower is found to be $60^\circ$ . Find the height of the tower and distance between the tower and the building.
On a horizontal plane there is a vertical tower with a flag pole on the top of the tower. At a point $9$ m away from the foot of the tower the angle of elevation of the top and bottom of the flag pole are $60^\circ$ and $30^\circ$ respectively. Find the height of the tower and the flag pole mounted on it.
A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle $30^\circ$ with the ground. The distance between the foot of the tree to the point where the top touches the ground is $8$ m. Find the height of the tree.
From a point $P$ on the ground the angle of eleveation of a $10$ m tall building is $30^\circ$ . A flag is hoisted at the top of the building and the angle of elevation of the top of the flag from $P$ is $45^\circ$ . Find the length of flag and the distance of building from point $P$ .
A $1.6$ m tall girl stands at a distance $3.2$ m from a lamp post. The length of the shadow of the girl is $4.8$ m on the ground. Find the height of the lamp post by using trigonometric ratios and similar triangles.
A $1.5$ m tall boy is standing some distance from a $30$ m tall building. The angle of elevation from his eyes to the top of the building increases from $30^\circ$ to $60^\circ$ as he walks towards the building. Find the distance he walks towards the building.
The shadow of a tower standing on level ground is found to be $40$ m longer when sun’s angle of elevation is $30^\circ$ than when it is $60^\circ$ . Find the height of the tower.
From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of a building $20$ m high are $45^\circ$ and $60^\circ$ respectively. Find the height of the transmission tower.
The angles of depression of the top and bottom of $8$ m tall building from the top of a multistoried building are $30^\circ$ and $45^\circ$ respectively. Find the height of the multistoried building and the distance between two buildings.
A statue $1.6$ m tall stands on the top of pedestal. From a point on the ground, the angle of elevation of the top of the statue is $60^\circ$ and from the same point the angle of elevation of the top of the pedestal is $45^\circ$ . Find the height of the pedestal.
From the top of a $7$ m high building, the angle of elevation of the top of a cable tower is $60^\circ$ and the angle of depression of its foot is $45^\circ$ . Determine the height of the tower.
As observed from the top of a $75$ m tall lighthouse, the angle of depression of two ships are $30^\circ$ and $45^\circ$ . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between two ships.
The angle of elevation of the top of the building from the foot of a tower is $30^\circ$ and the angle of top of the tower from the foot of the building is $60^\circ$ . If the tower is $50$ m high, find the height of the building.
From a point on a bridge across river the angles of depression of the banks on opposite sides of the river are $30^\circ$ and $45^\circ$ . If the bridge is at a height of $30$ m find the width of the river.
Two poles of equal heights are standing opposite to each other on either side of the road which is $80$ m wide. From a point between them on the road the angle of elevation of the top of the poles are $60^\circ$ and $30^\circ$ respectively. Find the height of the poles and the distance of the point from the poles.
A man sitting at a height of $20$ m on a tall tree on a small island in middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point which the man is sitting on the tree on either side of the river are $60^\circ$ and $30^\circ$ respectively. Find the width of the river.
A vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height $7$ m. From a point on the plane, the angle of elevation of the bottom of the flag-staff is $30^\circ$ and that of the top of the flag-staff is $45^\circ$ . Find the height of the tower.
The length of the shadow of a tower standing on level plane is found to be $2x$ m longer when the sun’s altitude is $30^\circ$ than when it was $45^\circ$ . Prove that the height of tower is $x(\sqrt{3} + 1)$ m.
A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle of $30^\circ$ with the ground. The distance from the foot of the tree to the point where the top touches the ground is $10$ m. Find the height of the tree.
A balloon is connected to a meteorological ground station by a cable of length $215$ m inclined at $60^\circ$ to the horizontal. Determine the height of the balloon from the ground assuming there is no slack in the cable.
To men on either side of a cliff $80$ m high observe that angle of elevation of the top of the cliff to be $30^\circ$ and $60^\circ$ respectively. Find the distance between the two men.
Find the angle of the elevation of the sun (sun’s altitude) when the length of the shdow of a vertical pole is equal to its height.
An aeroplane is flying at a height of $210$ m. At some instant the angles of depression of two points in opposite directions on both the banks of the river are $45^\circ$ and $60^\circ$ . Find the width of the river.
The angle of elevation of the top of a chimney from the top of a tower is $60^\circ$ and the angle of depression of the foot of the chimney from the top of the tower is $30^\circ$ . If the height of the tower is $40$ m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke emitting chimney should be $100$ m. State if the height of the chimney meets the pollution norms.
Two ships are in the sea on either side of a lighthouse in such a way that ships and lighthouse are always in the same straight line. The angles of depression of two ships are observed from the top of the lighthouse are $60^\circ$ and $45^\circ$ respectively. If the height of the lighthouse is $200$ m, find the distance between the two ships.
The horizontal distance between two poles is $15$ m. The angle of depression of top of the first pole as seen from the top of second pole is $30^\circ$ . If the height of second pole is $24$ m, find the height of the first pole.
The angle of depression of two ships from the top of a lighthouse and on the same side of it are found to be $45^\circ$ and $30^\circ$ respectively. If the ships are $200$ m apart, find the height of lighthouse.
The angle of elevation of the top of a tower from two points at a distance of $4$ m and $9$ m from the base of the tower and in the same straight line are complementary. Prove that the height of the tower is $6$ m.
The horizontal distance between two trees of different heights is $60$ m. The angle of depression of the top of the first tree when seen from the top of the second tree is $45^\circ$ . If the height of the second tree is $80$ m, find the height of the first tree.
A flag-staff stands on the top of a $5$ m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is $60^\circ$ and from the same point, the angle of elevation of the top of the tower is $45^\circ$ . Find the height of the flag-staff.
The angle of elevation of the top of a vertical tower $PQ$ from a point $X$ on the ground is $60^\circ$ . At a point $Y, 40$ m vertically above $X$ , the angle of elevation of the top is $45^\circ$ . Calculate the height of the tower.
As observed from the top of a $150$ m tall lighthouse, the angle of depressions of two ships approaching it are $30^\circ$ and $45^\circ$ respectively. If one ship is directly behind the other, find the distance between two ships.
The angle of elevation of the top of a rock from the top and foot of a $100$ m high tower are $30^\circ$ and $45^\circ$ respectively. Find the height of the rock.
A straight highway leads to the foot of the tower of height $50$ m. From the top of the tower, the angles of depression of two cars standing on the highway are $30^\circ$ and $60^\circ$ respectively. What is distance between the cars and how far is each car from the tower?
From the top of a building $AB, 60$ m high, the angles of depression of the top and bottom of a vertical lamp post $CD$ are observed to be $30^\circ$ and $60^\circ$ respectively. Find (i) horizontal distance between $AB$ and $CD$ , (ii) the height of the lamp post, and (iii) the difference between heights of the building and lamp post.
Two boats approach a lighthouse mid sea from opposite directions. The angles of elevation of the top of the lighthouse from the two boats are $30^\circ$ and $45^\circ$ respectively. If the distance between the ships is $100$ m, find the height of the lighthouse.
The angle of elevation of a hill from the foot of a tower is $60^\circ$ and the angle of elevation of the top of the tower from the foot of the hill is $30^\circ$ . If the tower is $50$ m high, find the height of the hill.
A moving boat is observed from the top of a $150$ m high cliff moving away from the cliff. The angle of depression of the boat changes from $60^\circ$ to $45^\circ$ in $2$ min. Find the speed of the boat.
From the top of a $120$ m high tower, a man observes two cars on the opposite sides of the tower and in straight line with the base of the tower with angles of depression as $60^\circ$ and $45^\circ$ . Find the distance between the cars.
Two points $A$ and $B$ are on the same side of a tower and in the same straight line as its base. The angles of depression of these points from the top of tower are $60^\circ$ and $45\circ$ respectively. If the height of the tower is $15$ m, find the distance between the points.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height $h$ . At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are $\alpha$ and $\beta$ respectively. Prove that the height of the tower is $\frac{h\tan\alpha}{\tan\beta - \tan\alpha}$ .
The angles of elevation of the top of a tower from two points at distancces $a$ and $b$ meters from the base and in same straight line with it are complementary. Prove that the height of the tower is $\sqrt{ab}$ m.
Two stations due south of a leaning tower which leans towards north are at distance $a$ and $b$ from its foot. If $\alpha, \beta$ be the elevations of the top of the tower from these stations, prove that its inclination $\theta$ to the horizontal is given by $\cot\theta = \frac{b\cot\alpha - a\cot\beta}{b - a}$ .
If the angle of elevation of a cloud from a point $h$ meteres above a lake is $\alpha$ and the angle of depression of its reflection in the lake is $\beta$ , prove that the height of the cloud is $\frac{h(\tan\alpha + \tan\beta)}{\tan\beta - \tan\alpha}$ .
A round balloon of radius $r$ subtends an angle $\alpha$ at the eye of the observer while the angle of elevation of its center is $\beta$ . Prove that the height of the center of the balloon is $r\sin\beta\cosec\frac{\alpha}{2}$ .
The angle of elevation of a cliff from a fixed point is $\theta$ . After going a distance of $k$ m towards the top of the cliff at an angle of $\phi$ , it is found that the angle of elevation is $\alpha$ . Show that the height of the cliff is $\frac{k(\cos\phi - \sin\phi\cot\alpha)}{\cot\theta - \cot\alpha}$ m.
The angle of elevation of the top of a tower from a point $A$ due south of the tower is $\alpha$ and from $B$ due east of the tower is $\beta$ . If $AB = d$ , show that the height of the tower is $\frac{d}{\sqrt{\cot^2\alpha + \cot^2\beta}}$ .
The elevation of a tower at a station $A$ due north of it is $\alpha$ and at a station $B$ due west of $A$ is $\beta$ . Prove that the height of tower is $\frac{AB\sin\alpha\sin\beta}{\sqrt{\sin^2\alpha - \sin^2\beta}}$ .
A $1.2$ m tall girl spots a balloon moving with the wind in a horizontal line at a height of $88.2$ m from the ground. The angle of elevation from the eyes of the girl at any instant is $60^\circ$ . After some time, the angle of elevation is reduced to $30^\circ$ . Find the distance travelled by the balloon during the interval.
A straight highway leads to the foot of the tower. A man standing on the top of the tower observes a car at an angle of depression of $30^\circ$ , which is approaching the foot of tower with uniform speed. Six seconds later the angle of depression is found to be $60^\circ$ . Find the further time taken by the car to reach the foot of the tower.
A man on a cliff observes a boat at an angle of depression of $30^\circ$ which is apporaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of depression of the boat is found to be $60^\circ$ . Find the time taken by the boat to read the shore.
A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes $12$ min for the angle of depression to change from $30^\circ$ to $45^\circ$ , find the time taken by the car to reach the foot of the tower.
A fire in a building is reported to two fire stations, $20$ km apart from each other on a straight road. One fire station observes that the fire is at an angle $60^\circ$ to the the road and second fire station observes that the fire is at $45^\circ$ to the road. Which station’s fire-fighting team will reach sooner and how much would it have to travel?
A man on the deck of a ship is $10$ m above the water level. He observes that the angle of elevation of the top of a cliff is $45^\circ$ and the angle of depression of its base is $30^\circ$ . Calculate the distance of ship from the cliff and height of the cliff.
There are two temples, one on each bank of a river, just opposite to each other. One temple is $50$ m high. From the top of this temple, the angle of depression of the top and the bottom of the other temple are $30^\circ$ and $60^\circ$ respectively. Find the width of the river and the height of the other temple.
The angle of elevation of an aeroplane from a point on the ground is $45^\circ$ . After a flight of $15$ seconds, the elevation changes to $30^\circ$ . If the aeroplane is flyging at a height of $3000$ m, find the speed of the aeroplane.
An aeroplane flying horizontally $1$ km above the ground is observed at an elevation of $60^\circ$ . After $10$ seconds, its elevation is observed to be $30^\circ$ . Find the speed of the aeroplane in km/hr.
A tree standing on a horizontal plane is leaning towards east. At two points situated at distance $a$ and $b$ exactly due west of it, with angles of elevation to the top respectively $\alpha$ and $\beta$ . Prove that the height of of the top from the ground is $\frac{(b - a)\tan\alpha\tan\beta}{\tan\alpha - \tan\beta}$ .
The angle of elevation of a stationary cloud from a point $2500$ m above a lake is $15^\circ$ and the angle of depression of its reflection in the lake is $45^\circ$ . What is the height of the cloud above the lake level? (Use $\tan15^\circ = 0.268$ ).
If the angle of elevation of a cloud from a point $h$ meters above a lake is $\alpha$ and the angle of depression of its reflection in the lake is $\beta$ , prove that the distance of cloud from the point of observation is $\frac{2h\sec\alpha}{\tan\beta - \tan\alpha}$ .
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be $\alpha$ and $\beta$ . Show that the height in miles of aeroplane above the rooad is given by $\frac{\tan\alpha\tan\beta}{\tan\alpha + \tan\beta}$ .
$PQ$ is a post of given height $h$ , and $AB$ is a tower at some distance. If $\alpha$ and $\beta$ are the angles of elevation of $B$ , at $P$ and $Q$ respectively. Find the height of the tower and its distance from the post.
A ladder rests against a wall at an angle $\alpha$ to the horizontal. Its foot is pulled away from the wall through a distance $a$ , so that it slides a distance $b$ down the the wall making an angle $\beta$ with the horizontal. Show that $\frac{a}{b} = \frac{\cos\alpha - \cos\beta}{\sin\beta - \sin\alpha}$ .
A tower subtends an angle $\alpha$ at a point $A$ in the plane of its base and the angle of depression of the foot of the tower at a point $b$ m just above $A$ is $\beta$ . Prove that the height of the tower is $b\tan\alpha\cot\beta$ .
An observer, $1.5$ m tall, is $28.5$ m away from a tower $30$ m high. Determine the angle of elevation of the top of the tower from his eye.
From the top of a tower $h$ m high, the angles of depression of two objects, which are in line with the foot of tower are $\alpha$ and $\beta (\beta > \alpha)$ . Find the distance between two objects.
A window of house is $h$ m above the ground. From the window, the angles of elevation and depression of the top and bottom of the amother house situated on the opposite side of the lane are found to be $\alpha$ and $\beta$ respectively. Prove that the height of the house is $h(1 + \tan\alpha\cot\beta)$ m.
The lower windows of a house is at a height of $2$ m above the ground and its upper window is $4$ m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be $60^\circ$ and $30^\circ$ respectively. Find the height of the balloon above the ground.
A man standing south of a lamp-post observes his shadow on the horizontal plane to be $24$ ft. long. On walking eastward $300$ ft. he finds the shadow as $30$ ft. If his height is $6$ ft., obtain the height of the lamp post above the plane.
When the sun’s altitude increases from $30^\circ$ to $60^\circ$ , the length of the shadow of tower decreases by $5$ m. Find the height of the tower.
A man observes two objects in a straight line in the west. On walking a distance $c$ to the north, the objects subtend an angle $\alpha$ in front of him. On walking a further distance $c$ to the north, they subtend angle $\beta$ . Show that distance between the objects is $\frac{3c}{2\cot\beta - \cot\alpha}$ .
An object is observed from the points $A, B, C$ lying in a horizontal straight line which passes directly underneath the object. The angular elevation at $B$ is twice that at $A$ and at $C$ three times that of $A$ . If $AB = a, BC = b$ , show that the height of the object is $\frac{a}{2b}\sqrt{(a + b)(3b - a)}$ .
At the foot of a mountain the elevation of its summit is $45^\circ$ ; after ascending one kilometer towards the mountain upon an incline of $30^\circ$ , the elevation changes to $60^\circ$ . Find the height of the mountain.
A man observes that when he has walked $c$ m up an inclined plane, the angular depression of an object in a horizontal plane through the foot of the slope is $\alpha$ and when he walked a further distance of $c$ m, the depression is $\beta$ . Prove that the inclination of the slope to the horizon is the angle whose cotangent is $2\cot\beta - \cot\alpha$ .
A ladder rests against a vertical wall at an angle $\alpha$ to the horizontal. Its foot is pulled away from the wall through a distance $a$ so that it slides a distance $b$ down the wall making an angle $\beta$ with the horizontal. Show that $a = b\tan\frac{\alpha + \beta}{2}$ .
A balloon moving in a straight line passes vertically above two points $A$ and $B$ on a horizontal plane $1000$ m apart. When above $A$ has an altitude $60^\circ$ as seen from $B$ , and when above $B$ , $30^\circ$ as seen from $A$ . Find the distance from $A$ of the point at which it will strike the plane.
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is $60^\circ$ . When he retires $40$ m from the bank perpendicular to it, he finds the angle to be $30^\circ$ , find the height of the tree and the breadth of the river.
The angles of elevation of a bird flying in a horizontal straight line from a point at four consecutive observations are $\alpha, \beta, \gamma$ and $\delta$ , the observations being taken at equal intervals of time. Assuming that the speed of the bird is uniform, prove that $\cot^2\alpha - \cot^2\delta = 3(\cot^2\beta - \cot^2\gamma)$ .
At a point on a level plane a vertical tower subtends an angle $\alpha$ and a pole of height $h$ m at the top of the tower subtends an angle $\beta$ , show that the height of the tower is $h\sin\alpha\cosec\beta\cos(\alpha + \beta)$ m.
$AB$ is a vertical pole. The end $A$ is on the level ground. $C$ is the middle point of $AB$ . $P$ is a point on the level ground. The portion $CB$ subtends an angle $\beta$ at $P$ . If $AP = n.AB$ , then show that $\tan\beta = \frac{n}{2n^2 + 1}$ .
The angular depression of the top and the foot of a chimney as seen from the top of a second chimney, which is $150$ m high and standing on the same level as the first, are $\theta$ and $\phi$ respectively. Find the distance between their tops when $\tan\theta = \frac{4}{3}$ and $\tan\phi = \frac{5}{2}.$
The angular elevation of a tower $CD$ at a place $A$ due south of it is $30^\circ$ and at a place $B$ due west of $A$ , the elevation is $18^\circ$ . If $AB = a$ , show that the height of the tower is $\frac{a}{\sqrt{2 + 2\sqrt{5}}}$ .
The elevation of a tower due north of a station at $P$ is $\theta$ and at a station $Q$ due west of $P$ is $\phi$ . Prove that the height of tower is $\frac{PQ.\sin\theta\sin\phi}{\sqrt{\sin^\theta - \sin^2\phi}}$ .
The angle of elevation of a certain peak when observed from each end of a horizontal baseline of length $2a$ is found to be $\theta$ . When observed from the mid-point of the base, angle of elevation is $\phi$ . Prove that the height of the peak is $\frac{a\sin\theta\sin\phi}{\sqrt{\sin(\theta + \phi)\sin(\phi - \theta)}}$ .
The angles of elevation of the top of a hill as seen from three consecutive milestones of a straight road not passing through the foot of the hill are $\alpha, \beta, \gamma$ respectively. Show that the height of the hill is $\frac{\sqrt{2}}{\sqrt{\cot^2\alpha + \cot^2\gamma - 2\cot^2\beta}}$ .
A tower stands in a field whose shape is that of an equilateral triangle and whose sides are $80$ ft. It subtends an angle at three corners whose tangents are respectively $\sqrt{3} + 1, \sqrt{2}, \sqrt{2}$ . Fnd its height.
A man on a hill observers that three towers on a horizontal plane subtend equal angles at his eye and that the angles of depression of their bases are $\alpha, \beta, \gamma$ . If $a, b,, c$ be the heights of the tower, prove that $\frac{\sin(\beta - \gamma)}{a\sin\alpha} + \frac{\sin(\gamma - \alpha)}{b\sin\beta} + \frac{\sin(\alpha - \beta)}{c\sin\gamma} = 0$ .
A person walking along a canal observes that two objects are in the same line which is inclined at an angle $\alpha$ to the canal. He walks a distnce $c$ further and observes that the objects subtend their greatest angle $\beta$ . Show that their distance apart is $\frac{2c\sin\alpha\sin\beta}{\cos\alpha + \cos\beta}$ .
A flag-staff is fixed on the top of a tower standing on a horizontal plane. The angles subtended by the flag-staff at two points $a$ m apart, on the same side and on the same horizontal line through the foot of the tower are the same and equal to $\alpha$ . The angle subtended by the tower at the farthest point is $\beta$ , find the height of the tower and the length of the flag staff.
The angle of elevation of a cloud from a point $h$ ft. above the surface of a lake is $\theta$ , the anngle of depression of its reflection in the lake is $\phi$ . Prove that the height of the cloud is $\frac{h\sin(\theta + \phi)}{\sin(\phi - \theta)}$ .
A road is inclined at an angle $10^\circ$ to the vertical towards the sun. The height of the shadow on the horizontal ground is $2.05$ m. If the elevation of the sun is $38^\circ$ , find the length of the road.
When the sun’s altitude increases from $30^\circ$ to $60^\circ$ , the length of the shadow of a tower decreases by $30$ m. Find the height of the tower.
The shadow of a tower standing on a level is found to be $60$ m longer when the sun’s altitude is $30^\circ$ than when it is $45^\circ$ . Find the height of the tower.
A man on a cliff observes a boat at an angle of depression of $30^\circ$ , which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depresssion of the boat is found to be $60^\circ$ . Assuming that the boat sails at uniform speed, determine how much more time it will take to reach the shore.
An aeroplane when $3000$ m high passes vertically above another aeroplane at an instant when there angle of elevation at the same observation points are $60^\circ$ and $45^\circ$ respectively. How many meters higher is the one than the other.
The angles of elevation of an aeroplane at two consecutive milestones respectively are $\alpha$ and $\beta$ . Find the height of the plane taking it to be between the two milestones and just above the road.
The altitude of a certain rock is $47^\circ$ and after walking towards it $1000$ m up a slope inclined at $30^\circ$ to the horizon an observer finds its altitude to be $77^\circ$ . Find the height of the rock. ( $\sin47^\circ = .73135$ .)
A man observes that when he moves up a distance $c$ m on a slope, the angle of depression of a point on the horizontal plane from the base of the slope is $30^\circ$ and when he moves up further a distance $c$ m, then angle of depression of the point is $45^\circ$ . Obtain the angle of depression of the slope with the horizontal.
On level ground the angle of elevation of the top of the tower is $30^\circ$ . On moving $20$ m nearer the angle of elevation is $60^\circ$ . What is the height of the tower?
An air-pilot at a height $h$ m above the ground observes the angle of depression of the top and bottom of a tower to be $30^\circ$ and $60^\circ$ . Find the height of the tower.
From the top of a hill $200$ m high, the angles of depression of the top and the bottom of a pillar are $30^\circ$ and $60^\circ$ respectively. Find the height of the pillar and its distance from the hill.
A vertical pole consists of two parts, the lower part being one-third of the whole. The upper part subtends an angle whose tangent is $\frac{1}{2}$ at a point in a horizontal plane through the foot of the pole and $20$ m from it. Find the height of the pole.
A statue is $8$ m high standing on the top of a tower $64$ m high on the bank of a river subtends at a point $A$ on the opposite bank facing the tower, the same angle as subtended at the same point $A$ by a man $2$ m high standing at the base of of the tower. Show that the breadth of the river is $16\sqrt{6}$ m.
A statue $a$ m high placed on a column $b$ m high subtends the same angle as the column to an observer $h$ m high standing on the horizontal plane at a distance $d$ m from the foot of the column. Show that $(a - b)d^2 = (a + b)b^2 - 2b^2h - (a - b)h^2$ .
The angles of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at a distance $a$ and $b$ are complementary angles. Prove that the height of the tower is $\sqrt{ab}$ . If the line joining the two points subtend an angle $\theta$ at the top of the tower, show that $\sin\theta = \frac{a - b}{a + b}$ .
A pillar subtends at a point $d$ m apart from its foot the same angle as that subtended at the same point by a statue on the top. If the pillar is $h$ m high, show that the height of the status is $\frac{h(d^2 + h^2)}{d^2 - h^2}$ m.
A vertical tower $50$ ft. high stands on a sloping ground. The foot of the tower is at the same level as the middle point of a vertical flag pole. From the top of the tower the angle of depression of the top and the bottom of the pole are $15^\circ$ and $45^\circ$ respectively. Find the length of the pole.
An observer at an anti-aircraft post $A$ identifies an enemy aircraft due east of his post at an angle of elevation of $60^\circ$ . At the same instant a detection post $D$ situated $4$ km south of $A$ reports the aircraft at an elevation of $30^\circ$ . Calculate the altitude at which the aircraft is flying.
A flag staff $PN$ stands up right on level ground. A base $AB$ is measured at right angled to $AN$ such that the points $A, B, N$ lie in the same horizontal plane. If $\angle PAN = \alpha$ and $\angle PBN = \beta$ . Prove that the height of the flag staff is $\frac{AB.\sin\alpha\sin\beta}{\sqrt{\sin(\alpha + \beta)\sin(\alpha - \beta)}}$ .
A vertical pole is divided in the ratio $1:9$ by a mark on it. If the two parts subtend equal angle at a distance of $20$ m from the base of the pole, find the height of the pole. The lower part is shorter than the upper one.
A chimney leans towards north. At equal distances due north and south of it in a horizontal plane, the elevation of the top are $\alpha,\beta$ . Show that the inclination of the chimney to the vertical is $\tan^{-1}\left[\frac{\sin(\alpha - \beta)}{2\sin\alpha\sin\beta}\right]$ .
A flag staff $10$ m high stands in the center of an equilateral triangle which is horizontal. If each side of the triangle subtends an angle of $60^\circ$ at the top of flag staff. Prove that the length of the sides are $5\sqrt{6}$ m.
Two posts are $120$ m apart, and the height of one is double that of the other. From the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary. Find the height of the posts.
A pole $100$ ft. high stands at the center of an equilateral triangle each side of which subtends and angle of $60^\circ$ at the top of the pole. Find the side of the triangle.
An observer on a carriage moving with a speed $v$ along a straight road observes in one position that two distant trees are in the same line with him which is inclined at an angle $\theta$ to the road. After a time $t$ , he observes that the trees subtend their greatest angle $\phi$ . Show that the distance between the tree is $\frac{2vt\sin\theta\sin\phi}{\cos\theta + \cos\phi}$ .
$A$ and $B$ are two points on one bank of a straight river and $C$ and $D$ are two points on the other bank. The direction from $C$ to $D$ is the same as from $A$ to $B$ . If $AB = a, \angle CAD = \alpha, \angle DAB = \beta, \angle CBA = \gamma$ , prove that $CD = \frac{a\sin\alpha\sin\gamma}{\sin\beta\sin(\alpha + \beta + \gamma)}$ .
To measure the breadth $PQ$ of a river a man places himself at $R$ in the straight line $PQ$ produced through $Q$ and then walks $100$ m at right angles to this line. He then finds $PQ$ and $QR$ subtend angles $15^\circ$ and $25^\circ$ at his eye. Find the breadth of the river.
A bird is perched on the top of a tree $20$ m high and its elevation from a point on the ground is $45^\circ$ . It flies off horizontally straight away from the observer and in second the elevation of the bird is reduced to $30^\circ$ . Find its speed.
The angles of elevation of a balloon from two stations $2$ km apart and from a point halfway between them are observed to be $60^\circ, 30^\circ$ and $45^\circ$ respectively. Prove that the height of the balloon is $500\sqrt{6}$ m.
If the angular elevations of the tops of two spires which appear in a straight line is $\alpha$ and the angular depression of their reflections in a lake, $h$ ft. below the point of observation are $\beta$ and $\gamma$ , show that the distance between the two spires is $2h\cos^2\alpha\sin(\gamma - \beta){\rm cosec}(\beta - \alpha){\rm cosec}(\gamma - \alpha)$ ft. where $\gamma > \beta$ .
A pole stands vertically on the center of a square. When $\alpha$ is the elevation of the sun its shadow just reaches the side of the square and is at a distance $x$ and $y$ from the ends of that side. Show that the height of the pole is $\sqrt{\frac{x^2 + y^2}{2}}.\tan\alpha$ .
A circular plate of radius $a$ touches a vertical wall. The plate is fixed horizontally at a height $b$ above the ground. A lighted candle of length $c$ stands vertically at the center of the plate. Prove that the breadth of the shadow on the wall where it meets the horizontal ground is $\frac{2a}{c}\sqrt{b^2 + 2bc}$ .
The extremity of the shadow of a flag-staff which is $6$ m high and stands on the top of a pyramid on a square base, just reaches the side of the base and is distant $x$ and $y$ ft. respectively from the ends of that side; prove that the height of the pyramid is $\sqrt{\frac{x^2 + y^2}{2}}.\tan\alpha - 6$ , where $\alpha$ is the elevation of the sun.
A man observes a tower $PQ$ of height $h$ from a point $C$ on the ground. He moves forward a distance $d$ towards the foot of the tower and finds that the angle of elevation has doubled. He further moves a distance $\frac{3}{4}d$ in the same direction. He finds that the angle of elevation is three times that at $P$ . Prove that $36h^2 = 35d^2$ .
A $2$ m long object is fired vertically upwards from the mid-point of two locations $A$ and $B, 8$ m apart. The speed of the object after $t$ seconds is given by $\frac{ds}{dt} = (2t + 1)$ m/s. Let $\alpha$ and $\beta$ be the angles subtended by the object at $A$ and $B$ respectively after one and two seconds. Find the value of $\cos(\alpha - \beta)$ .
A sign-post in the fom of an isosceles triangle $ABC$ is mounted on a pole of height $h$ fixed to the ground. The base $BC$ of the triangle is parallel to the ground. A man standing on the ground at distance $d$ from the sign-post finds that the top vertex $A$ of the triangle subtends an angle $\beta$ and either of the two vertices subtends the same angle $\alpha$ at his feet. Find the area of the triangle.
A tower is observed from two stations $A$ and $B$ , where $B$ is east of $A$ at a distance $100$ m. The tower is due north of $A$ and due north-west of $B$ . The angles of elevations of the tower from $A$ and $B$ are complementary. Find the height of the tower.
Two vertical poles whose heights are $a$ and $b$ subtend the samme angles $\alpha$ at a point in the line joining their feet. If they subtend angle $\beta$ and $\gamma$ at any point in the horizontal plane at which the line joining their feet subtends a right angle, prove that $(a + b)^2\cot^2\alpha = a^2\cot^2\beta + b^2\cot^2\gamma$ .
$PQ$ is a vertical tower. $P$ is the foot and $Q$ is the top of the tower. $A, B, C$ are three points in the horizontal plane through $P$ . The angles of elevation of $Q$ from $A, B, C$ are equal and each is equal to $\theta$ . The sides of the $\triangle ABC$ are $a, b, c$ and the area of the $\triangle ABC$ is $\Delta$ . Show that the height of the tower is $\frac{abc\tan\theta}{4\Delta}$ .
An observer at $O$ notices that the angle of elevation of the top of a tower is $90^\circ$ . The line joining $O$ to the base of the tower makes an angle of $\tan^{-1}\frac{1}{\sqrt{2}}$ with the north and is inclined eastwards. The observer travels a distance of $300$ m towards north to a point $A$ and finds the toewr to his east. The angle of elevation of the top of the tower at $A$ is $\phi$ . Find $\phi$ and the height of the tower.
A tower $AB$ leans towards west making an angle $\alpha$ with the vertical. The angular elevation of $B$ , the top most point of the tower, is $\beta$ as observed from a point C due west of $A$ at a distance $d$ from $A$ . If the angular elevation of $B$ from a point $D$ due east of $C$ at $a$ distance $2d$ from $C$ is $\gamma$ , then prove that $2\tan\alpha = 3\cot\beta - \cot\gamma$ .
The elevation of the top of a tower at point $E$ due east of the tower is $\alpha$ , and at a point $S$ due south of the tower is $\beta$ . Prove that it’s elevation $\theta$ at a point mid-way between $E$ and $S$ is given by $\cot^2\beta + \cot^2\alpha = 4\cot^2\theta$ .
A vertical tree stands at a point $A$ on a bank of a canal. The angle of elevation of its top from a point $B$ on the other bank of the canal and directly opposite to $A$ is $60^\circ$ . The angle of elevation of the top from another point $C$ is $30^\circ$ . If $A, B$ and $C$ are on the same horizontal plane, $\angle ABC = 120^\circ$ and $BC = 20$ m, find the height of the tree and the width of the canal.
A person observes the top of a vertical tower of height $h$ from a station $S_1$ and finds $\beta_1$ is the angle of elevation. He moves in a horizontal plane to second station $S_2$ andd finds that $\angle PS_2S_1$ is $\gamma_1$ and the angle subtended by $S_2S_1$ at $P$ (top of the tower) is $\delta_1$ and the angle of elevation is $\beta_2$ . He moves again to a third station $S_3$ such that $S_3S_2 = S_2S_1, \angle PS_3S_2 = \gamma_2$ and the angle subtended by $S_3S_2$ is $\delta_2$ . Show that $\frac{\sin\gamma_1\sin\beta_1}{\sin\delta_1} = \frac{\sin\gamma_2\sin\beta_2}{\sin\delta_2} = \frac{h}{S_1S_2}$ .
A straight pillar $PQ$ stands at a point $P$ . The points $A$ and $B$ are situated due south and east of $P$ respectively. $M$ is mid-point of $AB$ . $PAM$ is an equilateral triangle and $N$ is the foot of the perpendicular from $P$ on $AB$ . Suppose $AN = 20$ m and the angle of elevation of the top of the pillar at $N$ is $\tan^{-1}2$ . Find the height of the pillar and the angle of elevation of its top at $A$ and $B$ .
$ABC$ is a triangular park with $AB = AC = 100$ m. A television tower stands at the mid point of $BC$ . The angles of elevation of the top of the tower at $A, B$ and $C$ are $45^\circ, 60^\circ$ and $60^\circ$ respectively. Find the height of the tower.
A square tower stands upon a horizontal plane from which three of the upper corners are visible, their angular elevations are $45^\circ, 60^\circ$ and $45^\circ$ . If $h$ be the height of the tower and $a$ is the breadth of its sides, then show that $\frac{h}{a} = \frac{\sqrt{6}(1 + \sqrt{5})}{4}$ .
A right circular cylindrical tower of height $h$ and radius $r$ stands on a horizontal plane. Let $A$ be a point in the horizontal plane and $PQR$ be a semi-circular edge of the top of the tower such that $Q$ is the point in it nearest to $A$ . The angles of elevation of the points $P$ and $Q$ are $45^\circ$ and $60^\circ$ respectively. Show that $\frac{h}{r} = \frac{\sqrt{3}(1 + \sqrt{5})}{2}$ .
A is the foot of the vartical pole, $B$ and $C$ are due east of $A$ and $D$ is due south of $C$ . The elevation of the pole at $B$ is double that $C$ and the angle subtended by $AB$ at $D$ is $\tan^{-1}\frac{1}{5}$ . Also, $BC = 20$ m, $CD = 30$ m, find the height of the pole.
A person wishing to ascertain the height of a tower, stations himself on a horizontal plane through its foot at a point at which the elevation of the top is $30^\circ$ . On walking a distance $a$ in a certain direction he finds that elevation to the top is same as before, and on walking a distance $\frac{5}{3}a$ at right angles to his former direction, he finds the elevation of the top to be $60^\circ$ , prove that the height of the tower is either $\sqrt{\frac{5}{6}}a$ or $\sqrt{\frac{85}{48}}a$ .
A tower stands in a field whose shape is that of an equilateral triangle and whose side is $80$ ft. It subtends angles at three corners whose tangents are respectively $\sqrt{3} + 1, \sqrt{2}, \sqrt{2}$ . Find its height.
A flag-staff on the top of a tower is observed to subtend the same angle $\alpha$ at two points on a horizontal plane, which lie on a line passing through the center of the base of the tower annd whose distance from one another is $2a$ , and angle $\beta$ at a point half way between them. Prove that the heirght of the flag-staff is $a\sin\alpha\sqrt{\frac{2\sin\beta}{\cos\alpha\sin(\beta - \alpha)}}$ .
A man standing on a plane observes a row of equal and equidistant pillars, the $10$ -th and $17$ -th of which subtend the same angle that they would do if they were in position of the first respectively $\frac{1}{2}$ and $\frac{1}{3}$ of their height. Prove that, neglecting the height of the man’s eye, the line of pillars is inclined to be line drawn from his eye to the first at an angle whose secant is nearly $2.6$ .
A tower stands on the edge of the circular lake $ABCD$ . The foot of the tower is at $D$ and the angle of elevation of the top from $A, B, C$ are respectively $\alpha, \beta, \gamma$ . If $\angle BAC = \angle ACB = \theta$ . Show that $2\cos\theta\cot\beta = \cot\alpha + \cot\gamma$ .
A pole stands at the bank of circular pond. A man walking along the bank finds that angle of elevation of the top of the pole from the points $A$ and $B$ is $30^\circ$ and from the third point $C$ is $45^\circ$ . If the distance from $A$ to $B$ and from $B$ to $C$ measured along bank are $40$ m and $20$ m respectively. Find the radius of the pond and the height of the pole.
A man standing on the sea shore observes two buoys in the same direction, the line through them making an angle $\alpha$ with the shore. He then walks a distance along the shore a distance $a$ , when he finds the buoys subtend an angle $\alpha$ at his eye; and on walking a further distance $b$ he finds that they subtend an angle $\alpha$ at his eye. Show that the distance between the buoys is $\left(a + \frac{b}{2}\right)\sec\alpha - \frac{2a(a + b)}{2a + b}\cos\alpha$ , assuming the shore to be straight and henglecting the height of the man’s eye above the sea.
A railway curve in the shape of a quadrant of a circle, has $n$ telegraph posts at its ends and at equal distance along the curve. A man stationed at a point on one of the extreme radii produced sees the $p$ -th and $q$ -th posts from the end nearest him in a straight line. Show that the radius of the curve is $\frac{a}{2}\cos(p + q)\phi{\rm cosec}p\phi{\rm cosec}q\phi$ , where $\phi = \frac{\pi}{4(n - 1)}$ and $a$ is the distance from the man to the nearest end of curve.
A wheel with diameter $AB$ touches the horizontal ground at the point $A$ . There is a rod $BC$ fixed at $B$ such that $ABC$ is vertical. A man from a point $P$ on the ground, in the same plane as that of wheel and at a distance $d$ from $A$ , is watching $C$ and finds its angle of elevation is $\alpha$ . The wheel is then rotated about its fixed center $O$ such that $C$ moves away from the man. The angle of elevation of $C$ when it is about to disappear is $\beta$ . Find the radius of the wheel and the length of the rod. Also, find distance $PC$ when $C$ is just to disappear.
A semi-circular arch $AB$ of length $2L$ and a vertical tower $PQ$ are situated in the same vertical plane. The feet $A$ and $B$ of the arch and the base $Q$ of the tower are on the same horizontal level, with $B$ between $A$ and $Q$ . A man at $A$ finds the tower hidden from his view due to arch. He starts carwling up the arch and just sees the topmost point $P$ of the tower after covering a distance $\frac{L}{2}$ along the arch. He crawls further to the topmost point of the arch and notes the angle of elevation of $P$ to be $\theta$ . Compute the height of the tower in terms of $L$ and $\theta$ .
A circle passes through three points $A, B$ and $C$ with the line segment $AC$ as its diameter. A line passing through $A$ intersects the chord $BC$ at a point $D$ inside the circle. If angles $DAB$ and $CAB$ are $\alpha$ and $\beta$ respectively and the distance between point $A$ and the mid-point of the line segment $DC$ is $d$ . Prove that the area of the circle is $\frac{\pi d^2\cos^2\alpha}{\cos^2\alpha + \cos^2\beta + 2\cos\alpha\cos\beta\cos(\beta - \alpha)}$ .
The angle of elevation of a cloud from a point $h$ m above a lake is $\alpha$ , and the angle of depression of its reflection is $\beta$ . Prove that the distance of the observer from the cloud is $\frac{2h\cos\beta}{\sin(\beta - \alpha)}$ .
An isosceles triangle of wood is placed in a vertical plane, vertex upwards and faces the the sun. If $2a$ be the base of the triangle, $h$ its height and $30^\circ$ be the altitude of the sun, prove that the tangent of the angle at the apex of the shadow is $\frac{2ah\sqrt{3}}{3h^2 - a^2}$ .
A rectangular target faces due south, being vertical and standing on a horizontal plane. Compute the area of the target with that of its shadow on the ground when the sun is $\beta^\circ$ from the south at an altitude of $\alpha^\circ$ .
The extremity of the shadow of a flag staff which is $6$ m high and stands on the top of a pyramid on a square base just reaches the side of the base and is distant $56$ m and $8$ m respectively from the extremeties of that side. Find the sun’s altitude if the height of the pyramid is $34$ m.
The shdadow of a tower is observed to be half the known height of the tower and sometime afterwards is equal to the known height; how much will the sun have gone down in the interval. Given $\log 2 = 0.30103, \tan63^\circ23' = 10.3009994$ and diff for $1' = 3152$ .
A man notices two objects in a straight line due west. After walking a distance $c$ due north, he observes that the objects subtend an angle $\alpha$ at his eye; and after walking a further distance $2c$ due norht an angle $\beta$ . Show that the distance between the objects $\frac{8c}{3\cot\beta - \cot\alpha}$ . Ignore the height of the man.
A stationary balloon is observed from three points $A, B$ and $C$ on the plane ground and it is found that its angle of elevation from each of these points is $\alpha$ . If $\angle ABC = \beta$ and $AC = b$ , find the height of the balloon.
A lighthouse, facing north, sends out a fan-shaped beam of light extending from north-east to north-west. An observer on a steamer, sailing due west first sees the light when he is $5$ km away from the lighthouse and continues to see it for $30\sqrt{2}$ minutes. What is the speed of the steamer?
A man walking due north observes that the elevation of a balloon, which is due east of him and is sailing towards the north-west is then $60^\circ$ ; after he has walked $400$ yards the balloon is vertically over his head. Find its height, supposing it to have always remained the same.
A flag-staff stands on the middle of a square tower. A man on the ground opposite the middle of the face and distant from it $100$ m, just sees the flag; on receeding another $100$ m the tangents of the elevation of the top of the tower and the top of the flag staff are found to be $\frac{1}{2}$ and $\frac{5}{9}$ . Find the dimensions of the tower and the height of the flag staff, the ground being horizontal.
A vertical pole stands at a point $O$ on horizontal ground. $A$ and $B$ are points on the ground, $d$ meters apart. The pole subtends angles $\alpha$ and $\beta$ at $A$ and $B$ respectively. $AB$ subtends an angle $\gamma$ at $O$ . Find the height of the pole.
A vertical tree stands on a hill side that makes an angle $\alpha$ with the horizontal. From a point directly up the hill from the tree, the angle of elevation of the tree top is $\beta$ . From a point $m$ cm further up the hill the angle of depression of the tree top is $\gamma$ . If the tree is $h$ meters tall, find $h$ in terms of $\alpha, \beta, \gamma$ .
A person stands on the diagnal produced of the square base of a church tower, at a distance $2a$ from it and observes the angle of elevation of each of the two outer corners of the top of the tower to be $30^\circ$ , while that of the nearest corner is $45^\circ$ . Prove that the breadth of the tower is $a(\sqrt{10} - \sqrt{2})$ .
The elevation of a steeple at a place due south of it is $45^\circ$ and at another place due west of the former place is $15^\circ$ . If the distance between the two places be $a$ , prove that the height of steeple is $\frac{a(\sqrt{3} - 1)}{2.\sqrt[4]{3}}$ or $\frac{a}{\sqrt{6 + 4\sqrt{3}}}$ .
A tower surmounted by a spire stands on a level plane. A person on the plain observes that when he is at a distance $a$ from the foot of the tower, its top is in line with that of a mountain behind the spire. From a point at a distance $b$ further from the tower, he finds that the spire subtends the same angle as before at his eye and its top is in line with that of the mountain. If the height of the tower above the horizontal plane through the observer’s eye is $c$ , prove that the height of the mountain above the plane is $\frac{abc}{c^2 - a^2}$ .
From the bottom of a pole of height $h$ , the angle of elevation of the top of the tower is $\alpha$ . The pole subtends angle $\beta$ at the top of the tower. Find the height of the tower.
A man moves along the bank of a canal and observes a tower on the other bank. He finds that the angle of elevation of the top of the tower from each of the two points $A$ and $B$ , at a distance $6d$ apart is $\alpha$ . From a third point $C$ , between $A$ and $B$ at a distance $2d$ from $A$ , the angle of elevation is found to be $\beta$ . Find the height of the tower and width of the canal.
The angle of elevation of a balloon from two stations $2$ km apart and from a point halfway between them are observed to be $60^\circ, 30^\circ$ annd $45^\circ$ respectively. Prove that the height of the balloon is $500\sqrt{6}$ meters.
A flag staff $10$ meters high stands in the center of an equilateral triangle which is horizontal. If each side of the triangle subtends an angle of $60^\circ$ at the top of the flag staff. Prove that the length of the side of the triangle is $5\sqrt{6}$ meters.
A tower standing on a cliff subtends an angle $\beta$ at each of two stations in the same horizontal line passing through the base of the cliff and at a distance of $a$ meters and $b$ meters respectively from the cliff. Prove that the height of the tower is $(a + b)\tan\beta$ meters.
A man walking towards a tower $AB$ on which a flag staff is fixed observes that when he is at a point $E$ , distance $c$ meters from the tower, the flag staff subtends its greatest angle. If $\angle BEC = \alpha$ , prove that the heights of the tower and flag staff are $c\tan\left(\frac{\pi}{4} - \frac{\alpha}{2}\right)$ and $2c\tan\alpha$ meters respectively.
Four ships $A, B, C$ and $D$ are at sea in the following positions. $B$ is on a straight line segment $AC$ , $B$ is due north of $D$ and $D$ is due west of $C$ . The distance between $B$ and $D$ is $2$ km. If $\angle BDA = 40^\circ, \angle BCD = 25^\circ$ , what is the distance between $A$ and $D$ ? ( $\sin25^\circ = 0.423$ )
A train is moving at a constant speed at an angle $\theta$ east of north. Observations of the train are made from a fixed point. It is due north at some instant. Ten minutes earlier its bearing was $\alpha_1$ west of north whereas ten minutes afterwards its nearing is $\alpha_2$ east of north. Find $\tan\theta$ .
A man walks in a horizontal circle round the foot of a flag staff, which is inclined to the vertical, the foot of the flag staff being the center of the circle. The greatest and least angles which the flag staff subtends at his eyes are $\alpha$ and $\beta$ ; and when he is mid-way between the corresponding position the angle is $\theta$ . If the man’s height be neglected, prove that $\tan\theta = \frac{\sqrt{\sin^2(\alpha - \beta) + 4\sin^2\alpha\sin^2\beta}}{\sin(\alpha + \beta)}$ .
A bird flies in a circle on a horizontal plane. An observer stands at a point on the ground. Suppose $60^\circ$ and $30^\circ$ are the maximum and the minimum angles of elevation of the bird and that they occur when the bird is at point $P$ and $Q$ respectively on its path. Let $\theta$ be the angle of elevation of the bird when it is at a point on the arc of the circle exactly midway between $P$ and $Q$ . Find the numerical value of $\tan^2\theta$ . (Assume that the observer is not inside the vertical projection of the path of the bird).
A hill on a level plane has the form of a portion of a sphere. At the bottom the surface slopes at an angle $\alpha$ and from a point on the plane distant $a$ from the foot of the hill the elevation of the heighest visible point is $\beta$ . Prove that the height of the hill above the plane is $\frac{a\sin\beta\sin^2\frac{\alpha}{2}}{\sin^2\frac{\alpha - \beta}{2}}$ .
A hill standing on a horizontal plane, has a circular base and forms a part of a sphere. At two points on the plane, distant $a$ and $b$ from the base, the angular elevation of the heighest visible points on the hill are $\theta$ and $\phi$ . Prove that the height of the hill is $2\left[\frac{\sqrt{b\cot\frac{\phi}{2}} - \sqrt{a\cot\frac{\theta}{2}}}{\cot\frac{\theta}{2} - \cot\frac{\phi}{2}}\right]^2$ .
On the top of a hemispherical dome of radius $r$ there stands a flag of height $h$ . From a point on the ground the elevation of the top of the flag is $30^\circ$ . After moving a distant $d$ towards the dome, when the flag is just visible, the elevation is $45^\circ$ . Find $r$ and $h$ in terms of $d$ .
A man walks on a horizontal plane a distance $a$ , then through a distance $a$ at an angle $\alpha$ with his previous direction. After he has done this $n$ times, the change of his direction being always in the same sense, show that he is distant $\frac{a\sin(n\alpha/2)}{\sin(\alpha/2)}$ from his starting point and that this distance makes an angle $(n - 1)\frac{\alpha}{2}$ with his original direction.
In order to find the dip of a stream of coal below the surface of the ground, vertical borings are made from the angular point $A, B, C$ of a triangle $ABC$ which is in a horizontal plane; the depths of a stratum at these points are found to be $x, x + y$ and $x + z$ respectively. Show that the dip $\theta$ of the stratum which is assumed to be a plane is given by $\tan\theta\sin A = \sqrt{\frac{y^2}{c^2} + \frac{z^2}{b^2} - \frac{2yz}{bc}\cos A}$ .