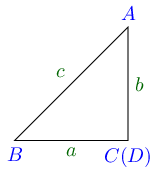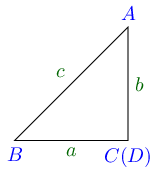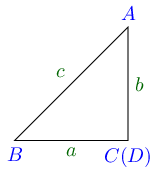16. Properties of TrianglesIn this chapter we will study the relations between the sides and trigonometrical ratios of the angles of a triangle. We already
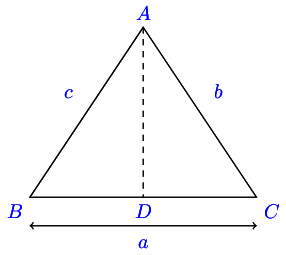
know that a triangle has three sides and three angles. In a △ A B C \triangle ABC △ A BC B A C , C B A , A C B BAC, CBA, ACB B A C , CB A , A CB A , B , C A, B, C A , B , C a , b , c a, b, c a , b , c
Thus, B C = a , A C = b , A B = c BC = a, AC = b, AB = c BC = a , A C = b , A B = c
We will also denote the radius of the circumcircle of the △ A B C \triangle ABC △ A BC R R R △ . \triangle. △. A + B + C = 18 0 ∘ A + B + C = 180^\circ A + B + C = 18 0 ∘ a + b > c , b + c > a , c + a > b a + b > c, b + c > a, c + a >
b a + b > c , b + c > a , c + a > b
16.1. Sine Formula or Sine Rule or Law of SinesIn △ A B C , a sin A = b sin B = c sin C \triangle ABC, \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} △ A BC , s i n A a = s i n B b = s i n C c
Proof: Case I. When ∠ C \angle C ∠ C
From A A A A D ⊥ B C . AD \perp BC. A D ⊥ BC . △ A B D , \triangle ABD, △ A B D ,
sin B = A D A B = A D c ⇒ A D = c sin B \sin B = \frac{AD}{AB} = \frac{AD}{c}\Rightarrow AD = c\sin B sin B = A B A D = c A D ⇒ A D = c sin B
From △ A C D , \triangle ACD, △ A C D ,
sin C = A D A C = A D b ⇒ A D = b sin C \sin C = \frac{AD}{AC} = \frac{AD}{b}\Rightarrow AD = b\sin C sin C = A C A D = b A D ⇒ A D = b sin C
Thus, c sin B = b sin C c\sin B = b\sin C c sin B = b sin C
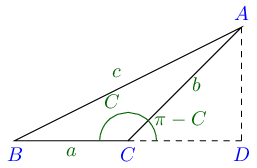
Case II. When ∠ C \angle C ∠ C
From A A A A D ⊥ B C . AD \perp BC. A D ⊥ BC . △ A B D , \triangle ABD, △ A B D ,
sin B = A D A B = A D c ⇒ A D = c sin B \sin B = \frac{AD}{AB} = \frac{AD}{c}\Rightarrow AD = c\sin B sin B = A B A D = c A D ⇒ A D = c sin B
From △ A C D , \triangle ACD, △ A C D ,
sin ( π − C ) = A D A C = A D b ⇒ A D = b sin C \sin(\pi - C) = \frac{AD}{AC} = \frac{AD}{b}\Rightarrow AD = b\sin C sin ( π − C ) = A C A D = b A D ⇒ A D = b sin C
Thus, c sin B = b sin C c\sin B = b\sin C c sin B = b sin C
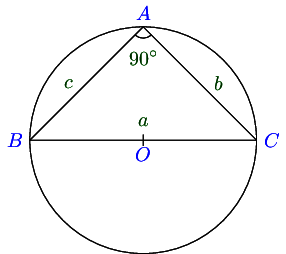
Case III. When ∠ C \angle C ∠ C 9 0 ∘ 90^\circ 9 0 ∘
From A A A A D ⊥ B C . AD \perp BC. A D ⊥ BC . △ A B D , \triangle ABD, △ A B D ,
sin B = A D A B = A D c ⇒ A D = c sin B \sin B = \frac{AD}{AB} = \frac{AD}{c}\Rightarrow AD = c\sin B sin B = A B A D = c A D ⇒ A D = c sin B
⇒ A C = c sin B [ ∵ C \Rightarrow AC = c\sin B[\because C ⇒ A C = c sin B [ ∵ C D D D ] ] ]
b = c sin B ⇒ b sin 9 0 ∘ = c sin B b = c\sin B \Rightarrow b\sin90^\circ = c\sin B b = c sin B ⇒ b sin 9 0 ∘ = c sin B
⇒ b sin C = c sin B \Rightarrow b\sin C = c\sin B ⇒ b sin C = c sin B
Thus, from all cases we have established that b sin B = c sin C \frac{b}{\sin B} = \frac{c}{\sin C} s i n B b = s i n C c
Similarly by drawing perpendicular from C C C A B , AB, A B ,
a sin A = b sin B \frac{a}{\sin A} = \frac{b}{\sin B} s i n A a = s i n B b
and thus
△ A B C , a sin A = b sin B = c sin C \triangle ABC, \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} △ A BC , s i n A a = s i n B b = s i n C c
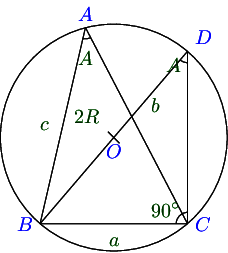
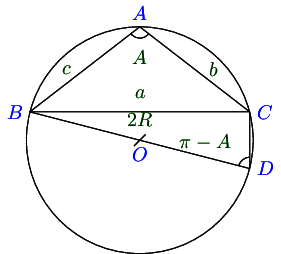
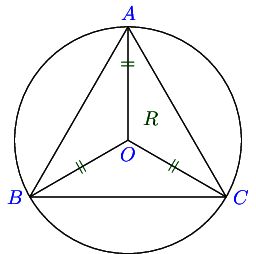
In △ A B C , a sin A = b sin B = c sin C = 2 R \triangle ABC, \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R △ A BC , s i n A a = s i n B b = s i n C c = 2 R R R R △ A B C \triangle ABC △ A BC
Case I. When ∠ A \angle A ∠ A
From △ B D C , \triangle BDC, △ B D C ,
sin A = B C B D = a 2 R ⇒ a sin A = 2 R \sin A = \frac{BC}{BD} = \frac{a}{2R} \Rightarrow \frac{a}{\sin A} = 2R sin A = B D BC = 2 R a ⇒ s i n A a = 2 R
Case II. When ∠ A \angle A ∠ A
From △ B D C , \triangle BDC, △ B D C ,
sin ( π − A ) = B C B D = a 2 R ⇒ a sin A = 2 R \sin (\pi - A) = \frac{BC}{BD} = \frac{a}{2R} \Rightarrow \frac{a}{\sin A} = 2R sin ( π − A ) = B D BC = 2 R a ⇒ s i n A a = 2 R
Case III. When ∠ A \angle A ∠ A 9 0 ∘ 90^\circ 9 0 ∘
From △ B D C , \triangle BDC, △ B D C ,
a = B C = 2 R ⇒ a sin A = 2 R a = BC = 2R \Rightarrow \frac{a}{\sin A} = 2R a = BC = 2 R ⇒ s i n A a = 2 R
Thus, in all three cases a sin A = 2 R \frac{a}{\sin A} = 2R s i n A a = 2 R
Similalry, by joining the diameter through A A A O O O C C C O , O, O , b sin B = 2 R \frac{b}{\sin B} = 2R s i n B b = 2 R c sin C = 2 R \frac{c}{\sin C} = 2R s i n C c = 2 R
Thus, a sin A = b sin B = c sin C = 2 R \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R s i n A a = s i n B b = s i n C c = 2 R
16.2. Tangent RuleIn any △ A B C , \triangle ABC, △ A BC ,
tan B − C 2 = b − c b + c cot A 2 , \tan \frac{B - C}{2} = \frac{b - c}{b + c}\cot \frac{A}{2}, tan 2 B − C = b + c b − c cot 2 A , tan A − B 2 = a − b a + b cot C 2 \tan \frac{A - B}{2} = \frac{a - b}{a + b}\cot
\frac{C}{2} tan 2 A − B = a + b a − b cot 2 C tan C − A 2 = c − a c + a cot B 2 \tan \frac{C - A}{2} = \frac{c - a}{c + a}\cot \frac{B}{2} tan 2 C − A = c + a c − a cot 2 B
Proof: By sine formula, a sin A = b sin B = c sin C = K \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = K s i n A a = s i n B b = s i n C c = K
∴ b = K sin B , c = k sin C \therefore b = K\sin B, c = k\sin C ∴ b = K sin B , c = k sin C
⇒ b − c b + c = K ( sin B − sin C ) K ( sin B + sin C ) = 2 cos B + C 2 sin B − C 2 2 sin B + C 2 cos B − C 2 \Rightarrow \frac{b - c}{b + c} = \frac{K(\sin B - \sin C)}{K(\sin B + \sin C)} = \frac{2\cos\frac{B + C}{2}\sin\frac{B -
C}{2}}{2\sin \frac{B + C}{2}\cos\frac{B - C}{2}} ⇒ b + c b − c = K ( s i n B + s i n C ) K ( s i n B − s i n C ) = 2 s i n 2 B + C c o s 2 B − C 2 c o s 2 B + C s i n 2 B − C
= cot B + C 2 tan B − C 2 = tan A 2 tan B − C 2 ⇒ tan B − C 2 = b − c b + c cot A 2 = \cot\frac{B + C}{2}\tan\frac{B - C}{2} = \tan\frac{A}{2}\tan \frac{B - C}{2} \Rightarrow \tan \frac{B - C}{2} = \frac{b -
c}{b + c}\cot \frac{A}{2} = cot 2 B + C tan 2 B − C = tan 2 A tan 2 B − C ⇒ tan 2 B − C = b + c b − c cot 2 A
Similarly, we can prove remaining two equations.
16.3. Cosine Formula or Cosine RuleIn any △ A B C , \triangle ABC, △ A BC ,
cos A = b 2 + c 2 − a 2 2 b c , cos B = c 2 + a 2 − b 2 2 c a , cos C = a 2 + b 2 − c 2 2 a b \cos A = \frac{b^2 + c^2 - a^2}{2bc}, \cos B = \frac{c^2 + a^2 - b^2}{2ca}, \cos C = \frac{a^2 + b^2 - c^2}{2ab} cos A = 2 b c b 2 + c 2 − a 2 , cos B = 2 c a c 2 + a 2 − b 2 , cos C = 2 ab a 2 + b 2 − c 2
Case I. When ∠ C \angle C ∠ C
A D = b sin C AD = b\sin C A D = b sin C
cos C = C D A C ⇒ C D = b cos C ⇒ B D = B C − C D = a − b cos C \cos C = \frac{CD}{AC} \Rightarrow CD = b\cos C \Rightarrow BD = BC - CD = a - b\cos C cos C = A C C D ⇒ C D = b cos C ⇒ B D = BC − C D = a − b cos C
Case II. When ∠ C \angle C ∠ C
A D = b sin ( π − C ) = b sin C AD = b\sin(\pi - C) = b\sin C A D = b sin ( π − C ) = b sin C
cos ( π − C ) = C D A C ⇒ C D = − b cos C ⇒ B D = B C + C D = a − b cos C \cos (\pi - C) = \frac{CD}{AC} \Rightarrow CD = -b\cos C \Rightarrow BD = BC + CD = a - b\cos C cos ( π − C ) = A C C D ⇒ C D = − b cos C ⇒ B D = BC + C D = a − b cos C
Case III. When ∠ C \angle C ∠ C 9 0 ∘ 90^\circ 9 0 ∘
Here, C C C D D D A D = A C = b = b sin C AD = AC = b = b\sin C A D = A C = b = b sin C
∠ C = 9 0 ∘ ∴ sin C = 1 \angle C = 90^\circ\therefore \sin C = 1 ∠ C = 9 0 ∘ ∴ sin C = 1
C D = 0 = b cos C ∵ cos C = cos 9 0 ∘ = 0 CD = 0 = b\cos C \because \cos C = \cos 90^\circ = 0 C D = 0 = b cos C ∵ cos C = cos 9 0 ∘ = 0
B D = B C − C D = a − b cos C BD = BC - CD = a - b\cos C B D = BC − C D = a − b cos C
Thus, in all cases A D = b sin C AD = b\sin C A D = b sin C B D = a − b cos C BD = a - b\cos C B D = a − b cos C
Now, A B 2 = A D 2 + B D 2 AB^2 = AD^2 + BD^2 A B 2 = A D 2 + B D 2
⇒ c 2 = b 2 sin 2 C + ( a − b cos C ) 2 = a 2 + b 2 − 2 a b cos C \Rightarrow c^2 = b^2\sin^2C + (a - b\cos C)^2 = a^2 + b^2 - 2ab\cos C ⇒ c 2 = b 2 sin 2 C + ( a − b cos C ) 2 = a 2 + b 2 − 2 ab cos C
cos C = a 2 + b 2 − c 2 2 a b \cos C = \frac{a^2 + b^2 - c^2}{2ab} cos C = 2 ab a 2 + b 2 − c 2
Similarly, we can prove it for ∠ A \angle A ∠ A ∠ B . \angle B. ∠ B .
16.5. Sub Angle RulesIn any △ A B C , \triangle ABC, △ A BC ,
sin A 2 = ( s − b ) ( s − c ) b c \sin \frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{bc}} sin 2 A = b c ( s − b ) ( s − c )
cos A 2 = s ( s − a ) b c \cos \frac{A}{2} = \sqrt{\frac{s(s - a)}{bc}} cos 2 A = b c s ( s − a )
t a n A 2 = ( s − b ) ( s − c ) s ( s − a ) tan \frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{s(s - a)}} t an 2 A = s ( s − a ) ( s − b ) ( s − c )
where 2 s = a + b + c 2s = a + b + c 2 s = a + b + c
Proof:
2 sin 2 A 2 = 1 − cos A = 1 − b 2 + c 2 − a 2 2 b c 2\sin^2\frac{A}{2} = 1 - \cos A = 1 - \frac{b^2 + c^2 - a^2}{2bc} 2 sin 2 2 A = 1 − cos A = 1 − 2 b c b 2 + c 2 − a 2
= 2 b c − b 2 − c 2 + a 2 2 b c = a 2 − ( b − c ) 2 2 b c = ( a + b − c ) ( a + c − b ) 2 b c = \frac{2bc - b^2 - c^2 + a^2}{2bc} = \frac{a^2 - (b - c)^2}{2bc} = \frac{(a + b - c)(a + c - b)}{2bc} = 2 b c 2 b c − b 2 − c 2 + a 2 = 2 b c a 2 − ( b − c ) 2 = 2 b c ( a + b − c ) ( a + c − b )
= ( 2 s − 2 c ) ( 2 s − 2 b ) 2 b c = 2 ( s − b ) ( s − c ) b c = \frac{(2s - 2c)(2s - 2b)}{2bc} = \frac{2(s - b)(s - c)}{bc} = 2 b c ( 2 s − 2 c ) ( 2 s − 2 b ) = b c 2 ( s − b ) ( s − c )
⇒ sin 2 A 2 = ( s − b ) ( s − c ) b c \Rightarrow \sin^2\frac{A}{2} = \frac{(s - b)(s - c)}{bc} ⇒ sin 2 2 A = b c ( s − b ) ( s − c )
⇒ sin A 2 = ± ( s − b ) ( s − c ) b c \Rightarrow \sin \frac{A}{2} = \pm\sqrt{\frac{(s - b)(s - c)}{bc}} ⇒ sin 2 A = ± b c ( s − b ) ( s − c )
But A 2 , \frac{A}{2}, 2 A , sin A 2 > 0 \sin \frac{A}{2} > 0 sin 2 A > 0
∴ sin A 2 = ( s − b ) ( s − c ) b c \therefore \sin \frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{bc}} ∴ sin 2 A = b c ( s − b ) ( s − c )
2 cos 2 A 2 = 1 + cos A = 1 + b 2 + c 2 − a 2 2 b c 2\cos^2\frac{A}{2} = 1 + \cos A = 1 + \frac{b^2 + c^2 - a^2}{2bc} 2 cos 2 2 A = 1 + cos A = 1 + 2 b c b 2 + c 2 − a 2
= ( b + c ) 2 − a 2 2 b c = ( a + b + c ) ( b + c − a ) 2 b c = \frac{(b + c)^2 - a^2}{2bc} = \frac{(a + b + c)(b + c - a)}{2bc} = 2 b c ( b + c ) 2 − a 2 = 2 b c ( a + b + c ) ( b + c − a )
= 2 s ( 2 s − 2 a ) 2 b c = 2 s ( s − a ) b c = \frac{2s(2s - 2a)}{2bc} = \frac{2s(s - a)}{bc} = 2 b c 2 s ( 2 s − 2 a ) = b c 2 s ( s − a )
⇒ cos 2 A 2 = s ( s − a ) b c \Rightarrow \cos^2\frac{A}{2} = \frac{s(s - a)}{bc} ⇒ cos 2 2 A = b c s ( s − a )
cos A 2 = ± s ( s − a ) b c \cos\frac{A}{2} = \pm\sqrt{\frac{s(s - a)}{bc}} cos 2 A = ± b c s ( s − a )
But A 2 \frac{A}{2} 2 A cos A 2 > 0 \cos\frac{A}{2} > 0 cos 2 A > 0
∴ cos A 2 = s ( s − a ) b c \therefore \cos\frac{A}{2} = \sqrt{\frac{s(s - a)}{bc}} ∴ cos 2 A = b c s ( s − a )
From 1 and 2 it follows that tan A 2 = ( s − b ) ( s − c ) s ( s − a ) \tan\frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{s(s - a)}} tan 2 A = s ( s − a ) ( s − b ) ( s − c )
Similarly, we can prove that sin B 2 = ( s − c ) ( s − a ) c a , sin C 2 = ( s − a ) ( s − b ) a b , \sin\frac{B}{2} = \sqrt{\frac{(s - c)(s - a)}{ca}}, \sin\frac{C}{2} = \sqrt{\frac{(s - a)(s -
b)}{ab}}, sin 2 B = c a ( s − c ) ( s − a ) , sin 2 C = ab ( s − a ) ( s − b ) , cos B 2 = s ( s − b ) c a , cos C 2 = s ( s − c ) a b , \cos\frac{B}{2} = \sqrt{\frac{s(s - b)}{ca}}, \cos\frac{C}{2} = \sqrt{\frac{s(s - c)}{ab}}, cos 2 B = c a s ( s − b ) , cos 2 C = ab s ( s − c ) , tan B 2 = ( s − c ) ( s − a ) s ( s − b ) , tan C 2 = ( s − a ) ( s − b ) s ( s − c ) \tan\frac{B}{2} = \sqrt{\frac{(s - c)(s - a)}{s(s - b)}}, \tan\frac{C}{2} = \sqrt{\frac{(s - a)(s - b)}{s(s - c)}} tan 2 B = s ( s − b ) ( s − c ) ( s − a ) , tan 2 C = s ( s − c ) ( s − a ) ( s − b )
16.6. Sines of Angles in Terms of SidesIn any △ A B C \triangle ABC △ A BC
sin A = 2 b c s ( s − a ) ( s − b ) ( s − c ) \sin A = \frac{2}{bc}\sqrt{s(s - a)(s - b)(s - c)} sin A = b c 2 s ( s − a ) ( s − b ) ( s − c )
sin B = 2 c a s ( s − a ) ( s − b ) ( s − c ) \sin B = \frac{2}{ca}\sqrt{s(s - a)(s - b)(s - c)} sin B = c a 2 s ( s − a ) ( s − b ) ( s − c )
sin C = 2 a b s ( s − a ) ( s − b ) ( s − c ) \sin C = \frac{2}{ab}\sqrt{s(s - a)(s - b)(s - c)} sin C = ab 2 s ( s − a ) ( s − b ) ( s − c )
Proof: sin A = 2 sin A 2 cos A 2 \sin A = 2\sin\frac{A}{2}\cos\frac{A}{2} sin A = 2 sin 2 A cos 2 A
= 2 ( s − b ) ( s − c ) b c s ( s − a ) b c = 2\sqrt{\frac{(s - b)(s - c)}{bc}}\sqrt{\frac{s(s - a)}{bc}} = 2 b c ( s − b ) ( s − c ) b c s ( s − a )
= 2 b c s ( s − a ) ( s − b ) ( s − c ) = \frac{2}{bc}\sqrt{s(s - a)(s - b)(s - c)} = b c 2 s ( s − a ) ( s − b ) ( s − c )
Similarly, we can prove it for other angles.
16.7. Area of a TriangleIf △ \triangle △ △ A B C , \triangle ABC, △ A BC ,
△ = 1 2 a b sin C = 1 2 b c sin A = 1 2 c a sin B \triangle = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B △ = 2 1 ab sin C = 2 1 b c sin A = 2 1 c a sin B
Proof: Case I. When ∠ C \angle C ∠ C
sin C = A D A C ⇒ A D = b sin C \sin C = \frac{AD}{AC} \Rightarrow AD = b\sin C sin C = A C A D ⇒ A D = b sin C
△ = 1 2 B C × A D = 1 2 a b sin C \triangle = \frac{1}{2}BC\times AD = \frac{1}{2}ab\sin C △ = 2 1 BC × A D = 2 1 ab sin C
Case II. When ∠ C \angle C ∠ C
sin ( π − C ) = A D A C ⇒ A D = b sin C \sin(\pi - C) = \frac{AD}{AC} \Rightarrow AD = b\sin C sin ( π − C ) = A C A D ⇒ A D = b sin C
△ = 1 2 B C × A D = 1 2 a b sin C \triangle = \frac{1}{2}BC\times AD = \frac{1}{2}ab\sin C △ = 2 1 BC × A D = 2 1 ab sin C
Case III. When ∠ C \angle C ∠ C 9 0 ∘ 90^\circ 9 0 ∘
△ = 1 2 B C × A D = 1 2 a b sin C [ ∵ C = 9 0 ∘ ∴ sin C = 1 ] \triangle = \frac{1}{2}BC\times AD = \frac{1}{2}ab\sin C[\because C=90^\circ \therefore \sin C = 1] △ = 2 1 BC × A D = 2 1 ab sin C [ ∵ C = 9 0 ∘ ∴ sin C = 1 ]
Thus, in all cases △ = 1 2 a b sin C \triangle = \frac{1}{2}ab\sin C △ = 2 1 ab sin C
Similarly, we can prove two other formulas.
16.7.1. Area in Terms of SidesIf △ \triangle △ △ A B C , \triangle ABC, △ A BC ,
△ = s ( s − a ) ( s − b ) ( s − c ) \triangle = \sqrt{s(s - a)(s - b)(s - c)} △ = s ( s − a ) ( s − b ) ( s − c )
Proof: △ = 1 2 a b sin C = 1 2 a b . 2 sin C 2 cos C 2 \triangle = \frac{1}{2}ab\sin C = \frac{1}{2}ab.2\sin\frac{C}{2}\cos\frac{C}{2} △ = 2 1 ab sin C = 2 1 ab .2 sin 2 C cos 2 C
= a b ( s − a ) ( s − b ) a b s ( s − c ) a b = s ( s − a ) ( s − b ) ( s − c ) = ab\sqrt{\frac{(s - a)(s - b)}{ab}}\frac{s(s - c)}{ab} = \sqrt{s(s - a)(s - b)(s - c)} = ab ab ( s − a ) ( s − b ) ab s ( s − c ) = s ( s − a ) ( s − b ) ( s − c )
16.7.1.1. Area in Terms of Radius of Circumcircle△ = 1 2 a b sin C = 1 2 a b . c 2 R = a b c 4 R \triangle = \frac{1}{2}ab\sin C = \frac{1}{2}ab.\frac{c}{2R} = \frac{abc}{4R} △ = 2 1 ab sin C = 2 1 ab . 2 R c = 4 R ab c
16.8. Tangent and Cotangent of Sub-angles of a TriangleIn any △ A B C , tan A 2 = ( s − b ) ( s − c ) △ , tan B 2 = ( s − a ) ( s − c ) △ , tan C 2 = ( s − a ) ( s − b ) △ , \triangle ABC, \tan\frac{A}{2} = \frac{(s - b)(s - c)}{\triangle}, \tan \frac{B}{2}= \frac{(s - a)(s -
c)}{\triangle}, \tan \frac{C}{2} = \frac{(s - a)(s - b)}{\triangle}, △ A BC , tan 2 A = △ ( s − b ) ( s − c ) , tan 2 B = △ ( s − a ) ( s − c ) , tan 2 C = △ ( s − a ) ( s − b ) , cot A 2 = s ( s − a ) △ , cot B 2 = s ( s − b ) △ , cot C 2 = s ( s − c ) t r i a n g l e \cot\frac{A}{2} = \frac{s(s - a)}{\triangle},
\cot\frac{B}{2} = \frac{s(s - b)}{\triangle}, \cot\frac{C}{2} = \frac{s(s - c)}{triangle} cot 2 A = △ s ( s − a ) , cot 2 B = △ s ( s − b ) , cot 2 C = t r ian g l e s ( s − c )
Proof: tan A 2 = ( s − b ) ( s − c ) s ( s − a ) = ( s − b ) 2 ( s − c ) 2 s ( s − a ) ( s − b ) ( s − c ) \tan\frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{s(s - a)}} = \sqrt{\frac{(s - b)^2(s - c)^2}{s(s - a)(s - b)(s -
c)}} tan 2 A = s ( s − a ) ( s − b ) ( s − c ) = s ( s − a ) ( s − b ) ( s − c ) ( s − b ) 2 ( s − c ) 2
= ( s − b ) ( s − c ) △ = \frac{(s - b)(s - c)}{\triangle} = △ ( s − b ) ( s − c )
Similarly, we can prove it for other angles and cotangents.
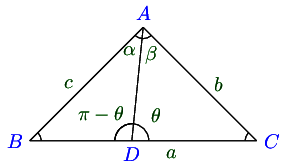
16.9. Dividing a Side in a RatioIf D D D B C BC BC △ A B C \triangle ABC △ A BC B D : D C = m : n BD:DC = m:n B D : D C = m : n ∠ A D C = θ , ∠ B A D = α \angle
ADC=\theta, \angle BAD=\alpha ∠ A D C = θ , ∠ B A D = α ∠ D A C = β , \angle DAC=\beta, ∠ D A C = β ,
( m + n ) cot θ = m cot α − n cot β (m + n)\cot\theta = m\cot\alpha - n\cot\beta ( m + n ) cot θ = m cot α − n cot β
( m + n ) cot θ = n cot B − m cot C (m + n)\cot\theta = n\cot B - m\cot C ( m + n ) cot θ = n cot B − m cot C
Proof:
∠ A D B = π − θ , ∠ A B D = π − ( α + π − θ ) = θ − α \angle ADB = \pi - \theta, \angle ABD = \pi - (\alpha + \pi - \theta) = \theta - \alpha ∠ A D B = π − θ , ∠ A B D = π − ( α + π − θ ) = θ − α
∠ A C D = π − ( θ + β ) \angle ACD = \pi - (\theta + \beta) ∠ A C D = π − ( θ + β )
From △ A B C , B D sin α = A D sin ( θ − α ) \triangle ABC, \frac{BD}{\sin\alpha} = \frac{AD}{\sin(\theta - \alpha)} △ A BC , s i n α B D = s i n ( θ − α ) A D
From △ A D C , D C sin ] b e t a = A D sin [ π − ( θ + β ) ] \triangle ADC, \frac{DC}{\sin]beta} = \frac{AD}{\sin[\pi - (\theta + \beta)]} △ A D C , s i n ] b e t a D C = s i n [ π − ( θ + β )] A D
⇒ D C sin β = A D sin ( θ + β ) \Rightarrow \frac{DC}{\sin\beta} = \frac{AD}{\sin(\theta + \beta)} ⇒ s i n β D C = s i n ( θ + β ) A D
Dividing, we get
B D sin β D C sin α = sin ( θ + β ) sin ( θ − α ) \frac{BD\sin\beta}{DC\sin\alpha} = \frac{\sin(\theta + \beta)}{\sin(\theta - \alpha)} D C s i n α B D s i n β = s i n ( θ − α ) s i n ( θ + β )
⇒ m sin β n sin ] α = sin ] t h e t a cos β + cos θ cos β sin θ cos α − cos θ sin α \Rightarrow \frac{m\sin\beta}{n\sin]\alpha} = \frac{\sin]theta\cos\beta + \cos\theta\cos\beta}{\sin\theta\cos\alpha - \cos\theta\sin\alpha} ⇒ n s i n ] α m s i n β = s i n θ c o s α − c o s θ s i n α s i n ] t h e t a c o s β + c o s θ c o s β
⇒ m sin θ sin β cos α − m cos θ sin α sin β = n sin α sin θ cos β + n sin α cos θ sin β \Rightarrow m\sin\theta\sin\beta\cos\alpha - m\cos\theta\sin\alpha\sin\beta = n\sin\alpha\sin\theta\cos\beta + n\sin\alpha\cos\theta\sin\beta ⇒ m sin θ sin β cos α − m cos θ sin α sin β = n sin α sin θ cos β + n sin α cos θ sin β
Dividing both sides by sin α sin β sin θ , \sin\alpha\sin\beta\sin\theta, sin α sin β sin θ ,
m cot α − m cot θ = n cot β + n cot θ m\cot\alpha - m\cot\theta = n\cot\beta + n\cot\theta m cot α − m cot θ = n cot β + n cot θ
⇒ ( m + n ) cot θ = m cot α − n cot β \Rightarrow (m + n)\cot\theta = m\cot\alpha - n\cot\beta ⇒ ( m + n ) cot θ = m cot α − n cot β
∠ B A D = 18 0 ∘ − ( 18 0 ∘ − θ + B ) = θ − B \angle BAD = 180^\circ - (180^\circ - \theta + B) = \theta - B ∠ B A D = 18 0 ∘ − ( 18 0 ∘ − θ + B ) = θ − B
∠ D A C = 18 0 ∘ − ( θ + C ) \angle DAC = 180^\circ - (\theta + C) ∠ D A C = 18 0 ∘ − ( θ + C )
From △ B A D , B D sin ( θ − B ) = A D sin B \triangle BAD, \frac{BD}{\sin(\theta - B)} = \frac{AD}{\sin B} △ B A D , s i n ( θ − B ) B D = s i n B A D
From △ A D C , D C sin ( 18 0 ∘ − ( θ + C ) ) = A D sin C \triangle ADC, \frac{DC}{\sin(180^\circ - (\theta + C))} = \frac{AD}{\sin C} △ A D C , s i n ( 18 0 ∘ − ( θ + C )) D C = s i n C A D
⇒ D C sin ( θ + C ) = A D sin C \Rightarrow \frac{DC}{\sin(\theta + C)} = \frac{AD}{\sin C} ⇒ s i n ( θ + C ) D C = s i n C A D
Dividing, we get
B D D C . sin ( θ + C ) sin ( θ − B ) = sin C sin B \frac{BD}{DC}.\frac{\sin(\theta + C)}{\sin(\theta - B)} = \frac{\sin C}{\sin B} D C B D . s i n ( θ − B ) s i n ( θ + C ) = s i n B s i n C
⇒ m b sin θ cos C + cos θ sin C sin θ cos B − cos θ sin B = sin C sin C \Rightarrow \frac{m}{b}\frac{\sin\theta\cos C + \cos\theta\sin C}{\sin\theta\cos B - \cos\theta\sin B} = \frac{\sin C}{\sin C} ⇒ b m s i n θ c o s B − c o s θ s i n B s i n θ c o s C + c o s θ s i n C = s i n C s i n C
Proceeding like previous proof, we get
( m + n ) cot θ = n cot B − m cot C (m + n)\cot\theta = n\cot B - m\cot C ( m + n ) cot θ = n cot B − m cot C
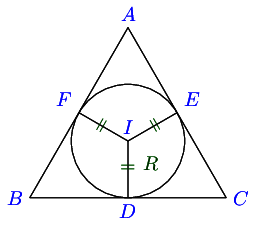
16.13. Distannces of Circum-center, In-center, Orthocenter and Centroid from VerticesWe have already shown that for circum-center distance is equal to circum-radius i.e. R R R
Referring to the image of in-circle, I F = r , ∠ F A I = A 2 IF = r, \angle FAI = \frac{A}{2} I F = r , ∠ F A I = 2 A
From right-angle triangle F I A , sin A 2 = r A I ⇒ A I = r cosec A 2 FIA, \sin\frac{A}{2} = \frac{r}{AI} \Rightarrow AI = r\cosec\frac{A}{2} F I A , sin 2 A = A I r ⇒ A I = r cosec 2 A
Similarly, B I = r cosec B 2 BI = r\cosec\frac{B}{2} B I = r cosec 2 B C I = r cosec C 2 CI = r\cosec\frac{C}{2} C I = r cosec 2 C
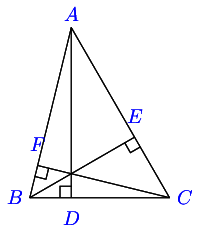
16.13.1. OrthocenterOrthocenter is point of intersection of perpendiculars from a vertex to opposite side.
Let the orthocenter be H H H
From right angle triangle A E B , cos A = A E A B ⇒ A E = c cos A AEB, \cos A= \frac{AE}{AB} \Rightarrow AE = c\cos A A EB , cos A = A B A E ⇒ A E = c cos A
From right angle triangle A D C , ∠ D A C = 9 0 ∘ − C ADC, \angle DAC = 90^\circ - C A D C , ∠ D A C = 9 0 ∘ − C
From right angle triangle A E H , cos ( 9 0 ∘ − C ) = A E A H AEH, \cos(90^\circ - C) = \frac{AE}{AH} A E H , cos ( 9 0 ∘ − C ) = A H A E
⇒ A H = c cos A sin C = 2 R cos A \Rightarrow AH = \frac{c\cos A}{\sin C} = 2R\cos A ⇒ A H = s i n C c c o s A = 2 R cos A
Similarly, B H = 2 R cos B , C H = 2 R cos C BH = 2R\cos B, CH=2R\cos C B H = 2 R cos B , C H = 2 R cos C
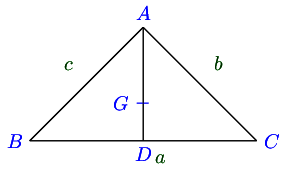
16.13.2. CentroidLet G G G A D . AD. A D .
From geometry, A B 2 + A C 2 = 2 D B 2 + 2 A D 2 AB^2 + AC^2 = 2DB^2 + 2AD^2 A B 2 + A C 2 = 2 D B 2 + 2 A D 2
⇒ c 2 + b 2 2. ( a 2 ) 2 + 2 A D 2 \Rightarrow c^2 + b^2 2.\left(\frac{a}{2}\right)^2 + 2AD^2 ⇒ c 2 + b 2 2. ( 2 a ) 2 + 2 A D 2
⇒ 2 A D 2 = 2 b 2 + 2 c 2 − a 2 2 \Rightarrow 2AD^2 = \frac{2b^2 + 2c^2 - a^2}{2} ⇒ 2 A D 2 = 2 2 b 2 + 2 c 2 − a 2
∵ A G : G D = 2 : 1 \because AG:GD = 2:1 ∵ A G : G D = 2 : 1 2 : 1 2:1 2 : 1
A G = 2 3 A D = 1 3 2 b 2 + 2 c 2 − a 2 AG = \frac{2}{3}AD = \frac{1}{3}\sqrt{2b^2 + 2c^2 - a^2} A G = 3 2 A D = 3 1 2 b 2 + 2 c 2 − a 2
Similarly, B G = 1 3 2 a 2 + 2 c 2 − b 2 , C G = 1 3 2 a 2 + 2 b 2 − c 2 BG = \frac{1}{3}\sqrt{2a^2 + 2c^2 - b^2}, CG = \frac{1}{3}\sqrt{2a^2 + 2b^2 - c^2} BG = 3 1 2 a 2 + 2 c 2 − b 2 , CG = 3 1 2 a 2 + 2 b 2 − c 2
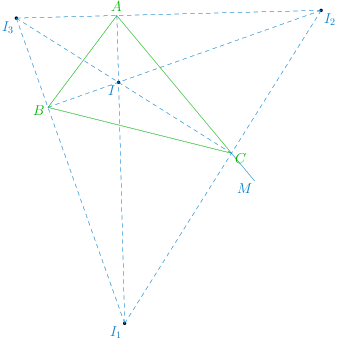
16.14. Esccribed TrianglesLet I I I I 1 , I 2 I_1,I_2 I 1 , I 2 I 3 I_3 I 3 A , B A, B A , B C C C I C IC I C ∠ A C B \angle ACB ∠ A CB I 1 C I_1C I 1 C B B B C C C ∠ B C M \angle BCM ∠ BCM
∴ I C I 1 = ∠ I C B + ∠ I C B \therefore ICI_1 = \angle ICB + \angle I_CB ∴ I C I 1 = ∠ I CB + ∠ I C B
= 1 2 A C B + 1 2 ∠ B C M = 9 0 ∘ = \frac{1}{2}ACB + \frac{1}{2}\angle BCM = 90^\circ = 2 1 A CB + 2 1 ∠ BCM = 9 0 ∘
Similarly, ∠ I C I 2 \angle ICI_2 ∠ I C I 2 ∠ I C I 3 \angle ICI_3 ∠ I C I 3
Hence, I 1 C I 2 I_1C_I2 I 1 C I 2 I C . IC. I C . I 2 A I 3 I_2AI_3 I 2 A I 3 I A , IA, I A , I 3 B I 1 I_3BI_1 I 3 B I 1 I B . IB. I B .
We also see that I A IA I A I 1 A I_1A I 1 A ∠ A \angle A ∠ A I 1 I A I_1IA I 1 I A I 2 I B I_2IB I 2 I B I 3 I C I_3IC I 3 I C
The △ I 1 I 2 I 3 \triangle I_1I_2I_3 △ I 1 I 2 I 3 excentric triangle of △ A B C \triangle ABC △ A BC
16.15. Distance between Orthocenter and CircumcenterLet O O O O F ⊥ A B OF\perp AB OF ⊥ A B H H H
∠ O A F = 9 0 ∘ − ∠ A O F = 9 0 ∘ − C \angle OAF = 90^\circ - \angle AOF = 90^\circ - C ∠ O A F = 9 0 ∘ − ∠ A OF = 9 0 ∘ − C
Let B L BL B L A C AC A C H . H. H .
∠ H A L = 9 0 ∘ − C \angle HAL = 90^\circ - C ∠ H A L = 9 0 ∘ − C
∠ O A H = A − ∠ O A F − ∠ H A L = A − ( 18 0 ∘ − 2 C ) = C − B \angle OAH = A - \angle OAF - \angle HAL = A - (180^\circ - 2C) = C - B ∠ O A H = A − ∠ O A F − ∠ H A L = A − ( 18 0 ∘ − 2 C ) = C − B
Also, O A = R OA = R O A = R H A = 2 R cos A HA = 2R\cos A H A = 2 R cos A
O H 2 = O A 2 + H A 2 − 2 O A . H A . cos O A H = R 2 + 4 R 2 cos 2 A − 4 R 2 cos A cos ( C − B ) OH^2 = OA^2 + HA^2 - 2OA.HA.\cos OAH = R^2 + 4R^2\cos^2A - 4R^2\cos A\cos(C - B) O H 2 = O A 2 + H A 2 − 2 O A . H A . cos O A H = R 2 + 4 R 2 cos 2 A − 4 R 2 cos A cos ( C − B )
= R 2 + 4 R 2 cos A [ cos A − cos ( C − B ) ] = R 2 − 8 R 2 cos A cos B cos C = R^2 + 4R^2\cos A[\cos A - \cos(C - B)] = R^2 - 8R^2\cos A\cos B\cos C = R 2 + 4 R 2 cos A [ cos A − cos ( C − B )] = R 2 − 8 R 2 cos A cos B cos C
O H = R 1 − 8 cos A cos B cos C OH = R\sqrt{1 - 8\cos A\cos B\cos C} O H = R 1 − 8 cos A cos B cos C
16.16. Distance between Incenter and CircumcenterLet O O O O F ⊥ A B . OF\perp AB. OF ⊥ A B . I I I I C ⊥ A B . IC\perp AB. I C ⊥ A B .
∠ O A F = 9 0 ∘ − C ∴ ∠ O A I = ∠ I A F − O A F = A 2 − 9 0 ∘ + C = C − B 2 \angle OAF = 90^\circ - C \therefore \angle OAI = \angle IAF - OAF = \frac{A}{2} - 90^\circ + C = \frac{C - B}{2} ∠ O A F = 9 0 ∘ − C ∴ ∠ O A I = ∠ I A F − O A F = 2 A − 9 0 ∘ + C = 2 C − B
Also, A I = I E sin A 2 = r sin A 2 = 4 R sin B 2 sin C 2 AI = \frac{IE}{\sin\frac{A}{2}} = \frac{r}{\sin\frac{A}{2}} = 4R\sin\frac{B}{2}\sin\frac{C}{2} A I = s i n 2 A I E = s i n 2 A r = 4 R sin 2 B sin 2 C
∴ O I 2 = O A 2 + A I 2 − 2. O A . A I . cos O A I \therefore OI^2 = OA^2 + AI^2 - 2.OA.AI.\cos OAI ∴ O I 2 = O A 2 + A I 2 − 2. O A . A I . cos O A I
= R 2 + 16 R 2 sin 2 B 2 sin 2 C 2 − 8 R 2 sin B 2 sin C 2 cos C − B 2 = R^2 + 16R^2\sin^2\frac{B}{2}\sin^2\frac{C}{2} - 8R^2\sin\frac{B}{2}\sin\frac{C}{2}\cos\frac{C - B}{2} = R 2 + 16 R 2 sin 2 2 B sin 2 2 C − 8 R 2 sin 2 B sin 2 C cos 2 C − B
O I = R 1 − 8 sin A 2 sin B 2 sin C 2 OI = R\sqrt{1 - 8\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}} O I = R 1 − 8 sin 2 A sin 2 B sin 2 C
= R 2 − 2 R r = \sqrt{R^2 - 2Rr} = R 2 − 2 R r
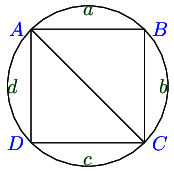
16.17. Area of a Cyclid QuadrilateralIf a , b , c , d a, b, c, d a , b , c , d s s s ( s − a ) ( s − b ) ( s − c ) ( s − d ) \sqrt{(s -
a)(s - b)(s - c)(s - d)} ( s − a ) ( s − b ) ( s − c ) ( s − d )
Proof: Let A B C D ABCD A BC D A B = a , B C = b , C D = c AB = a, BC = b, CD = c A B = a , BC = b , C D = c A D = d AD = d A D = d
Since opposing angles of a quadrilateral are complementary, therefore B + D = A + C = π B + D = A + C = \pi B + D = A + C = π
Applying cosine law in △ A B C , cos B = a 2 + b 2 − A C 2 2 a b ⇒ A C 2 = a 2 + b 2 − 2 a b cos B \triangle ABC, \cos B = \frac{a^2 + b^2 - AC^2}{2ab} \Rightarrow AC^2 = a^2 + b^2 - 2ab\cos B △ A BC , cos B = 2 ab a 2 + b 2 − A C 2 ⇒ A C 2 = a 2 + b 2 − 2 ab cos B
Similarly, in △ A C D , A C 2 = c 2 + d 2 − 2 c d cos ( π − B ) = c 2 + d 2 + 2 c d cos B \triangle ACD, AC^2 = c^2 + d^2 -2cd\cos(\pi - B) = c^2 + d^2 + 2cd\cos B △ A C D , A C 2 = c 2 + d 2 − 2 c d cos ( π − B ) = c 2 + d 2 + 2 c d cos B
From these two equations, we get cos B = a 2 + b 2 − c 2 − d 2 2 ( a b + c d ) \cos B = \frac{a^2 + b^2 - c^2 - d^2}{2(ab + cd)} cos B = 2 ( ab + c d ) a 2 + b 2 − c 2 − d 2
Area of quadrilateral A B C D ABCD A BC D △ A B C \triangle ABC △ A BC △ A C D \triangle ACD △ A C D
= 1 2 a d sin B + 1 2 c d sin ( π − B ) = 1 2 ( a b + c d ) sin B = \frac{1}{2}ad\sin B + \frac{1}{2}cd \sin(\pi - B) = \frac{1}{2}(ab + cd)\sin B = 2 1 a d sin B + 2 1 c d sin ( π − B ) = 2 1 ( ab + c d ) sin B
Also, sin 2 B = 1 − cos 2 B = 1 − [ a 2 + b 2 − c 2 − d 2 2 ( a b + c d ) ] 2 \sin^2B = 1 - \cos^2B = 1 - \left[\frac{a^2 + b^2 - c^2 - d^2}{2(ab + cd)}\right]^2 sin 2 B = 1 − cos 2 B = 1 − [ 2 ( ab + c d ) a 2 + b 2 − c 2 − d 2 ] 2
= ( 2 a b + 2 c d + a 2 + b 2 − c 2 − d 2 ) ( 2 a b + 2 c d − a 2 − b 2 + c 2 + d 2 ) 4 ( a b + c d ) 2 = \frac{(2ab + 2cd + a^2 + b^2 - c^2 - d^2)(2ab + 2cd - a^2 - b^2 + c^2 + d^2)}{4(ab + cd)^2} = 4 ( ab + c d ) 2 ( 2 ab + 2 c d + a 2 + b 2 − c 2 − d 2 ) ( 2 ab + 2 c d − a 2 − b 2 + c 2 + d 2 )
= [ ( a + b ) 2 − ( c − d ) 2 ] [ ( c + d ) 2 − ( a − b ) 2 ] 4 ( a b + c d ) 2 = \frac{[(a + b)^2 -(c - d)^2][(c + d)^2 - (a - b)^2]}{4(ab + cd)^2} = 4 ( ab + c d ) 2 [( a + b ) 2 − ( c − d ) 2 ] [( c + d ) 2 − ( a − b ) 2 ]
= 4 ( s − a ) ( s − b ) ( s − c ) ( s − d ) 4 ( a b + c d ) 2 = \frac{4(s - a)(s - b)(s - c)(s - d)}{4(ab + cd)^2} = 4 ( ab + c d ) 2 4 ( s − a ) ( s − b ) ( s − c ) ( s − d )
Thus, area of quadrilateral = ( s − a ) ( s − b ) ( s − c ) ( s − d ) = \sqrt{(s - a)(s - b)(s - c)(s - d)} = ( s − a ) ( s − b ) ( s − c ) ( s − d )