22. Properties of Triangles’ Solutions Part 5

201. Let the sides of the cyclid quadrilateral $ABCD$ having sides $AB = 3, BC = 3, CD = 4, DA = 4.$

     Join $B$ with $D.$ Clearly, $BD$ is diameter of circum-circle so it will subtend a right-angle at $A$ and $C.$

     Clearly $\triangle ABD\cong \triangle BCD$

     $\therefore BD = \sqrt{3^2 + 4^2} = 5$

     Thus, radius of the circumcircle $= 2.5$ cm

     Also, $AD + BC = AB + CD$

     $\therefore$ Area of the quadrilateral $= \sqrt{abcd} = 12$ sq. cm.

     We know that $12 = rs \Rightarrow r = 12/7$ cm where $r$ is radius of in-circle.

202. Let the quadrilateral be $ABCD$ and let points be $E, F, G, H, I, J, K, L$ on sides in order.

     $\therefore EF=FG=GH=HI=IJ=JK=KL=LE=x$

     By symmetry, $AE=AL=BG=BF=CH=CI=DJ=DK=a$

     Using Pythagoras theorem in $\triangle ALE,$

     $LE^2 = AL^2 + AE^2 \Rightarrow x^2 = \sqrt{2}a$

     $\therefore AB = a + x + a = 2a + x = 2$

     $\Rightarrow a = \frac{\sqrt{2}}{\sqrt{2} + 1}$

     $\Rightarrow x = \frac{2}{\sqrt{2} + 1}$

     Thus, length of each side of octagon is $\frac{2}{\sqrt{2} + 1}.$

203. Let the perimeter be $6a$ the sides of hexagon will be $a$ and sides of triangle will be $2a.$

     We know that for a regular polygon having $n$ sides with each side’s length $a$ the area is $\frac{na^2}{4}\cot\frac{\pi}{n}$

     Area of regular hexagon $= \frac{6a^2}{4}\cot30^\circ = \frac{3\sqrt{3}a^2}{2}$

     Area of equilateral triangle $= \frac{3.4a^2}{4}\cot60^\circ = \sqrt{3}a^2$

     $\therefore$ Ratio of areas $= 2/3$

204. Following the above problem $n = 3$

205. Ratio of areas $= \frac{3}{4}$

     $\therefore$ Ratio of sides $= \frac{\sqrt{3}}{2}$

     $\therefore$ Ratio of altitudes $= \sqrt{3}/2$

     $\Rightarrow \sin\theta = \sqrt{3}/2$

     $\theta = 60^\circ, 120^\circ$ so it is an equilateral triangle and a hexogon.

206. We know that angle of a polygon having $n$ sides is $(n - 2)\pi/n$

     Let there be $n$ sides in one polygon and $2n$ in another.

     Ratio $= \frac{2n - 2}{n - 2}.\frac{n}{2n} = \frac{9}{8}$

     $(n - 1)/n - 2 = 9/8 \Rightarrow n = 10 \Rightarrow 2n = 20$

207. The diagram is given below:

     

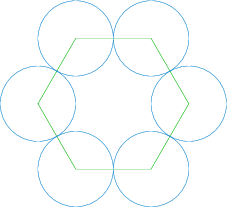
     The six touching circle will form a hexgon. The sector internal to hexgon is of angle $120^\circ.$ Side of hexagon will be double the radius of circles i.e. $2a$ as shown in figure.

     Area inside circles = Area of hexgon - 6*area of sector

     $= \frac{3\sqrt{3}}{2}4a^2 - 6.\frac{\pi a^2}{3} = 6\sqrt{3}a^2 - 2\pi a^2$

     $= 2a^2(3\sqrt{3} - \pi)$

208. Let $O$ is the radius of circumcircle of the square. Given, $AB = 1, BD = \sqrt{3}$ Also, $OA = OB = OD = 1$

     Thus, for $\triangle ABD, R = 1, \frac{a}{\sin A = 2R} = 2$

     $\frac{\sqrt{3}}{\sin A} = 2 \therefore A = 60^\circ$

     $\Rightarrow C = 120^circ$ [opposite angle in cyclic quadrilateral]

     By cosine law in $\triangle ABD$

     $3 = 1 + x^2 - 2x\cos60^\circ$

     $x^2 - x - 2 = 0 \Rightarrow x = 2$

     Thus, $\Delta = \frac{3\sqrt{3}}{4} = \frac{1}{2}1.2.\sin60^\circ + \frac{1}{2}c.d\sin60^\circ$

     $\therefore cd = 1$

     By cosine law in $\triangle BCD,$

     $3 = c^2 + d^2 - 2cd\cos 120^\circ \Rightarrow c^2 + d^2 = 2$

     $\Rightarrow c = d = 1$

     $BC = 1, CD = 1, AD = x = 2$

209. Let $AB = a, BC = b, CD = c, DA = d$

     In $\triangle ABC,$

     $AC^2 = a^2 + b^2 - 2ab\cos B$

     In $\triangle ADC,$

     $AC^2 = c^2 + d^2 - 2cd\cos D$

     $B + D = \pi$ [Angles opposite in a cyclic quadrilateral]

     $\Rightarrow AC^2(ab + cd) = (a^2 + b^2)cd + (c^2 + d^2)ab$

     Simirlarly, we can find $BD$ and then we find that

     $(AC.BD)^2 = (ac + bd)62$

     $\Rightarrow AC.BD = AB.CD + BC.AD$

210. Let $p$ be the perimeter of both the polygons. So the length of the sides will be $p/n$ and $p/2n.$ Let $A_1$ and $A_2$ denote the areas for them.

     $A_1 = \frac{1}{4}.n.\frac{p^2}{n^2}\cot\frac{\pi}{n}$

     $A_2 = \frac{1}{4}.2n.\frac{p^2}{4n^2}\cot\frac{\pi}{2n}$

     $\frac{A_1}{A_2} = \frac{2\cot\frac{\pi}{n}}{\cot\frac{\pi}{2n}}$

     $= \frac{2\cos\frac{\pi}{n}}{1 + \cos\frac{\pi}{2n}}$

211. Let $P = \sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}$ and $C$ is fixed.

     $P = \frac{1}{2}\left[\cos\frac{A - B}{2} - \cos\frac{A + B}{2}\right]\sin\frac{C}{2}$

     $= \frac{1}{2}\left[\cos \frac{A - B}{2} - \sin\frac{C}{2}\right]\sin\frac{C}{2}$

     As $C$ is fixed, the value $P$ will depend on the value of $\cos\frac{A - B}{2}$ and $P$ will be maxmimum when $A = B$

     Similalry, when $B$ is fixed $P$ will be maxed when $A = C,$ and when $A$ is fixed $P$ will be maxed when $B = C$

     Thus, $P$ will be maximum when $A = B = C = \pi/3$

     $\Rightarrow P_{max} = 1/8$

     Hence proved.

212. Let $A$ be the arithmetic mean. Then $A = \frac{\cos\left(\alpha + \frac{\pi}{2}\right) + \cos\left(\beta + \frac{\pi}{2}\right) + \cos\left(\gamma + \frac{\pi}{2}\right)}{3}$

     $= -\frac{\sin\alpha + \sin\beta + \sin\gamma}{3}$

     Clearly, $\sin\alpha + \sin\beta + \sin\gamma$ will be maximum when $\alpha = \beta = \gamma$ as proved in last problem making $A$ minimum.

     $\alpha + \beta + \gamma = 2\pi$

     $A_{min} = 3\sin\frac{2\pi}{3}.\frac{1}{3} = \frac{\sqrt{3}}{2}$

213. Let $\tan\frac{A}{2} = x, \tan\frac{B}{2} = y, \tan\frac{C}{2} = z$

     We know that $x^2 + y^2 + z^2 - xy - yz - xz \geq 0$

     $x^2 + y^2 + z^2 \geq xy + yz + xz$

     $A + B + C = \pi$

     $\Rightarrow \tan\left(\frac{A}{2} + \frac{B}{2}\right) = \cot\frac{C}{2}$

     $\Rightarrow \tan\frac{A}{2}\tan\frac{B}{2} + \tan\frac{B}{2}\tan\frac{C}{2} + \tan\frac{C}{2}\tan\frac{A}{2} = 1$

     $\Rightarrow xy + yz + xz = 1$

     $\Rightarrow x^2 + y^2 + z^2 \geq 1$

214. Given, $2b = (m + 1)a \Rightarrow m = \frac{2b}{a} - 1$

     $\Rightarrow \cos A = \frac{1}{2}\sqrt{\frac{(m - 1)(m + 3)}{m}}$

     $\Rightarrow \frac{b^2 + c^2 - a^2}{2bc} = \frac{1}{2}\sqrt{\frac{\left(\frac{2b}{a} - 2\right)\left(\frac{2b}{a} + 2\right)}{m}}$

     $\Rightarrow \frac{b^2 + c^2 - a^2}{(m + 1)ac} = \frac{1}{a}\sqrt{\frac{(b - a)(b + a)}{m}}$

     $\Rightarrow c^2\sqrt{m} - (m + 1)p.c + p^2\sqrt{m} = 0$

     This is a quadratic equation in $c$ and thus it will have two values.

     $\Rightarrow c_1, c_2 = p/m, \sqrt{m}p$

     $\Rightarrow c_2/c_1 = m$

215. Let $a, b, c$ be the sides of the triangle.

     $\Rightarrow s = (a + b + c)/2$ and $s - a, s- b, s - c$ will be all greater than zero.

     For positive quantities A.M. $>$ G.M.

     $\therefore \frac{s + s - a + s - b + s - c}{4} > [s(s - a)(s - b)(s - c)]^{1/4}$

     $\Rightarrow \frac{2s}{4}>\Delta^{1/2}$

     $\Rightarrow \Delta < \frac{s^2}{4}$

216. $A + B + C = \pi$

     $B + C = \pi - \frac{\pi}{4} \Rightarrow C = \frac{3\pi}{4} - B$

     Let $p = \tan A\tan B\tan C = \tan B\tan\left(3\pi/4 - B\right)$

     $p = \tan\frac{\tan3\pi/4 - \tan B}{1 + \tan3\pi/4\tan B}$

     $= \tan B\left(\frac{-1 - \tan B}{1 - \tan B}\right)$

     $p - p\tan B = -\tan B - \tan^2B$

     $\tan^2B + (1 - p)\tan B + p = 0$

     For $\tan B$ to be real, $D\geq 0$

     $\Rightarrow (1 - p)^2 - 4p \geq 0$

     $p = 3\pm 2\sqrt{2}$

     Clearly, both $B$ and $C$ both cannot be obtuse.

     If either of $B$ or $C$ is obtuse angle, then

     $\tan B\tan C < 0$ $\Rightarrow p < 0$

     If both are acute then

     $\pi/4 < B < \pi/2, \pi/4 < C < \pi/2$

     $\Rightarrow \tan B>1, \tan C> 1$

     $\Rightarrow \tan B\tan C > 1 \Rightarrow p > 1$

     $\Rightarrow p < 0, p\geq 3 + 2\sqrt{2}$

217. Let $ABC$ be a triangle and $AD, BE, CF$ be lines drawn from vertices to opposite sides such that $\angle ADC = \angle BES = \angle CFB = \alpha$

     Let the triangle formed by $AD, BE, CF$ be $A'B'C'$

     Clearly, $\angle B'A'C' = \angle FA'B = \pi - (\angle BFA' + \angle FBA') = \pi - [\alpha + \pi - (\alpha + A)] = A$

     Similarly, $\angle A'B'C'= B$ and $A'C'B' = C$

     Thus, $\triangle ABC ~ \triangle A'B'C'$

     $\frac{\text{Area of }\triangle A'B'C'}{\text{Area of }\triangle ABC} = \frac{B'C'^2}{a^2}$

     Applying sine rule in $AC'B,$

     $\frac{AC'}{\sin[\pi - (A + \alpha)]} = \frac{AB}{\sin(\pi - C)}$

     $\Rightarrow AC' = 2R\sin(A + \alpha)$

     Similarly, $BC' = 2R\sin(\alpha - A)$

     $\Rightarrow B'C' = AC' - AB' = 2a\cos\alpha$

     Thus, ratio of areas $= 4\cos^2\alpha:1$

218. Given, $a,b,c$ and $\Delta$ are rational.

     $s = (a + b + c)/2$ will be rational.

     $\tan\frac{B}{2} = \frac{\Delta}{s(s - a)}$ will be rational as all terms involved are rational.

     Similarly, $\tan\frac{C}{2}$ will be rational.

     $\sin B = \frac{2\tan\frac{B}{2}}{1 + \tan^2\frac{B}{2}}$ will be rational as $\tan\frac{B}{2}$ is rational.

     Likewise $\sin C$ will be rational.

     $\frac{A}{2} = 90^\circ - (C/2 + B/2)$

     $\tan\frac{A}{2} = \cot\left(\frac{B}{2} + \frac{C}{2}\right)$

     $= \frac{1 - \tan\frac{B}{2}\tan\frac{C}{2}}{\tan\frac{B}{2} + \tan\frac{C}{2}}$ will be rational as all the terms involved are rational.

     Thus, $\sin A$ will also be rational.

     $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$ are rational as all the terms involved are rational.

     $R = \frac{abc}{4\Delta} \Rightarrow \Delta = \frac{abc}{4R}$ will be rational as well.

219. Applying sine rule, $\frac{b}{\sin B} = \frac{c}{\sin C}$

     $\Rightarrow \frac{\sqrt{6}}{\sin 30^\circ} = \frac{4}{\sin C}$

     $\sin C = \frac{2}{\sqrt{6}} < 1$

     So $C$ may be acute or obtuse.

     We observed that $b < c \Rightarrow B < C,$ so $B$ may be acute or obtuse.

     If $C$ is obtuse $B$ may be acute. Hence two triangles are possible.

     Applying cosine rule, $\cos B = \frac{c^2 + a^2 - b^2}{2ac} = \frac{16 + a^2 - 6}{2.4.a}$

     $\frac{\sqrt{3}}{2} = \frac{10 + a^2}{8a} \Rightarrow a^2 - 4\sqrt{3}a + 10 = 0$

     $a = 2\sqrt{3}\pm 2$

     $\therefore \Delta_1, \Delta_2 = \frac{1}{2}a.c.\sin30^\circ = 2\sqrt{3}\pm\sqrt{2}$

220. Let $\triangle ABC$ be the equilateral triangle such that its sides have length $a.$

     $s = \frac{3a}{2}, \Delta = \frac{\sqrt{3}}{2}a$

     $r = \frac{\Delta}{s} = \frac{a}{2\sqrt{3}}$

     Diameter of incircle will be diagonal of inscribed square i.e. $2r = \frac{a}{\sqrt{3}}$

     Thus, side of square $= \frac{a}{\sqrt{6}}$

     $\therefore$ Area of square $= \frac{a^2}{6}$

221. Given, $AD = \frac{abc}{b^2 - c^2}$

     Also, $AD = b\sin 23^\circ \Rightarrow \frac{abc}{b^2 - c^2} = b\sin23^\circ$

     $\Rightarrow \frac{ac}{b^2 - c^2} = \sin23^\circ$

     $\Rightarrow \frac{\sin A\sin C}{\sin^2B - \sin^2C} = \sin23^\circ$

     $\Rightarrow \frac{\sin C\sin 23^\circ}{\sin(B + C)\sin(B - C)} = \sin23^\circ$

     $\Rightarrow \sin(B - 23^\circ) = 1 = \sin90^\circ$

     $\Rightarrow B = 113^\circ$

222. Given $a:b:c = 4:5:6 \Rightarrow a = 4k, b = 5k, c = 6k$ (let)

     $\frac{R}{r} = \frac{abc}{4\Delta}.\frac{s}{\Delta} = \frac{abc.\frac{a + b + c}{2}}{4.s(s - a)(s - b)(s - c)}$

     $= \frac{16}{7}$

223. Let $\angle BAD = \alpha, \angle CAD = \beta$

     Applying sine law in $\triangle ADB, \frac{BD}{\sin\alpha} = \frac{AD}{\sin B}$

     $\Rightarrow AD = \frac{BD}{\sin\alpha}.\frac{\sqrt{3}}{2}$

     Applying sine law in $\triangle ADC, \frac{CD}{\sin\beta} = \frac{AD}{\sin C}$

     $\Rightarrow AD = \frac{CD}{\sin\beta}.\frac{1}{\sqrt{2}}$

     $\Rightarrow \frac{BD}{CD}.\frac{\sqrt{3}}{\sqrt{2}} = \frac{\sin\alpha}{\sin\beta}$

     $\Rightarrow \frac{\sin\alpha}{\sin\beta} = \frac{1}{\sqrt{6}}$

224. Given, $3\sin x - 4\sin^2x - k = 0$

     $\sin3x = k$

     Since $A$ and $B$ satisfy the equations $\therefore \sin3A = \sin3B = k$

     $\sin3A - \sin3B = 0$

     $\therefore -2\sin\frac{3C}{2}\sin\frac{3(A - B)}{2} = 0$

     Since $A\neq B$ and also both $A$ and $B$ are less that $\pi/3[\because 0<k<1]$

     $\Rightarrow \sin\frac{3C}{2} = 0 \Rightarrow C = \frac{2\pi}{3}$

225. Since $A,B,C$ are in A.P. $\therefore 2B = A + C$

     $A + B + C = \pi \Rightarrow B = \pi/3$

     $\sin(2A + B) = \frac{1}{2} = \sin\frac{\pi}{6}$

     $\Rightarrow 2A + B = n\pi + (-1)^n\frac{\pi}{6}$

     $A = \frac{\pi}{4},\frac{11\pi}{12}$ these are the values between $0$ and $\pi.$

     But $\frac{11\pi}{12}$ is not possible as $B = \pi/3$

     $\therefore A = \pi/4$

226. Let $ABC$ be the triangle having right angle at $B$. From question, $AC = 2\sqrt{2}BD$

     Let $BD = x \therefore AC = 2\sqrt{2}x$ and $\angle C = \theta$

     $\tan C = \frac{BD}{CD} = \frac{x}{CD}\Rightarrow CD = x\cot\theta$

     $\tan(90^\circ - C) = \frac{BD}{AD} \therefore AD = x\tan\theta$

     $AD + CD = AC \Rightarrow \tan\theta + \cot\theta = 2\sqrt{2}$

     $\Rightarrow 2\sin\theta\cos\theta = \frac{1}{\sqrt{2}}$

     $\Rightarrow \sin2\theta = \sin\frac{\pi}{4}$

     $\Rightarrow \theta = \frac{\pi}{8}, \frac{3\pi}{8}$

     $\Rightarrow A = \frac{3\pi}{8}, \frac{\pi}{8}$

227. $P + Q + R = \pi$

     $\therefore P + Q = \pi/2 [\because R = \pi/2]$

     $\Rightarrow \tan\left(\frac{P + Q}{2}\right) = 1$

     $\Rightarrow \tan\frac{P}{2} + \tan\frac{Q}{2} = 1 - \tan\frac{P}{2}\tan\frac{Q}{2}$

     Since $\tan\frac{P}{2}$ and $\tan\frac{Q}{2}$ are roots of the equation $ax^2 + bx + c = 0$

     $\Rightarrow \tan\frac{P}{2} + \tan\frac{Q}{2} = -\frac{b}{a}, \tan\frac{P}{2}\tan\frac{Q}{2} = \frac{c}{2}$

     $\Rightarrow -\frac{b}{a} = 1 - \frac{c}{a}$

     $\Rightarrow a + b = c$

228. Let $AD$ be the median such that $\angle BAD = 30^\circ, \angle DAC = 45^\circ$ and $\angle ADC = \theta$

     Applying $mn$ theorem, we get

     $2\cot\theta = \cot30^\circ - \cot45^\circ$

     $\Rightarrow \tan\theta = \sqrt{3} + 1$

     $\sin C = \frac{\sqrt{3} + 2}{\sqrt{2}\sqrt{5 + 2\sqrt{3}}}$

     Applying sine law in $\triangle ADC,$ we get

     $\frac{AD}{\sin C} = \frac{DC}{\sin45^\circ}$

     $\Rightarrow DC = 1$

     $\Rightarrow DC = BD = 1 \Rightarrow BC = 2$

229. We know that in a triangle $\tan A + \tan B + \tan C = \tan A + \tan B + \tan C$

     Also, since A.M $\geq$ G.M.

     $\Rightarrow \frac{\tan A + \tan B + \tan C}{3}\geq \sqrt[3]{\tan A\tan B\tan C}$

     $\Rightarrow \tan A\tan B\tan C\geq 3\sqrt[3]{\tan A\tan B\tan C}$

     $\Rightarrow \tan^2A\tan^2B\tan^2C\geq 27$

     $\Rightarrow \tan A + \tan B + \tan C\geq 3\sqrt{3}$

230. Given, $\cos\frac{A}{2} = \frac{1}{2}\sqrt{\frac{b}{c} + \frac{c}{b}}$

     $\sqrt{\frac{s(s - a)}{bc}} = \frac{1}{2}\sqrt{\frac{b}{c} + \frac{c}{b}}$

     $\frac{(a + b + c)(b + c - a)}{4bc} = \frac{b^2 + c^2}{4bc}$

     $\Rightarrow a^2 = 2bc$

     Thus, square described on side $a$ is twice the rectangle contained by two other sides.

231. Given, $\cos\theta = \frac{a - b}{c} \Rightarrow \sin\theta = \frac{1}{c}\sqrt{c^2 - (a - b)^2}$

     $\frac{(a + b)\sin\theta}{2\sqrt{ab}} = \frac{(a + b)\sqrt{c^2 - (a - b)^2}}{2c\sqrt{ab}}$

     $\frac{(a + b)\sqrt{2ab(1 - \cos C)}}{2c\sqrt{ab}} = \frac{a + b}{\sqrt{2}c}.\sqrt{2}\sin\frac{C}{2}$

     $= \frac{\sin A + \sin B}{\sin C}.\sin\frac{C}{2}$

     $= \cos\frac{A - B}{2}$

     $\frac{c\sin\theta}{2\sqrt{ab}} = \frac{c\sqrt{c^2 - (a - b)^2}}{2\sqrt{ab}}$

     $= \frac{c\sqrt{2ab(1 - \cos C)}}{2\sqrt{ab}} = \sin \frac{C}{2} = \cos \frac{A + B}{2}$

232. We have proven earlier that distance between circumcenter and incenter is $\sqrt{R^2 - 2rR}$

     Clearly, $\sqrt{R^2 - 2rR}\geq 0$

     $\Rightarrow R\geq 2r$

233. Given, $\tan B = \cos A$

     $\Rightarrow \frac{\sqrt{1 - \cos^2B}}{\cos B} = \cos A$

     $\Rightarrow \cos^2B = \frac{1}{2 - \sin^2A}$

     Also given that $\cos C = \tan A$

     $\Rightarrow \tan^2 C = \frac{1 - 2\sin^2A}{\sin^2A}$

     Now given that $\cos B = \tan C$

     $\Rightarrow \frac{1}{2 - \sin^2A} = \frac{1 - 2\sin^2A}{\sin^2A}$

     $\Rightarrow \sin A = \pm\sqrt{\frac{3\pm\sqrt{5}}{2}}$

     Same value will be obtained for $\sin B$ and $\sin C$ and that is equal to $2\sin 18^\circ$

234. $A + B + C = 180^\circ$

     $\Rightarrow \cos(A + B) = -\cot C$

     $\Rightarrow \cot A\cot B + \cot B\cot C + \cot C\cot A = 1$

     Now $\cot^2A + \cot^2B + \cot^2C - 1 = \cot^2A + \cot^2B + \cot^2C - (\cot A\cot B + \cot B\cot C + \cot C\cot A)$

     $= \frac{1}{2}[(\cot A - \cot B)^2 + (\cot B - \cot C)^2 + (\cot C - \cot A)^2] \geq 0$

     $\Rightarrow \cot^2A + \cot^2B + \cot^2C \geq 1$

235. We have proven in 229 that $\tan A + \tan B + \tan C \geq 3\sqrt{3}$

     We apply A.M. $\geq$ G.M. again on $\tan^2A, \tan^2B, \tan^2C$

     $\frac{\tan^2A + \tan^2B + \tan^2C}{3}\geq (\tan^2A\tan^B\tan^2C)^{1/3}$

     $\Rightarrow \tan^2A + \tan^2B + \tan^C \geq 9$

236. We know that in a $\triangle ABC, \sin\frac{A}{2} + \sin\frac{B}{2} + \sin\frac{C}{2} \leq \frac{3}{2}$

     Now we know that A.M. $\geq$ H.M.

     $\frac{\cosec\frac{A}{2} + \cosec\frac{B}{2} + \cosec\frac{C}{2}}{3}\geq \frac{3}{\sin\frac{A}{2} + \sin\frac{B}{2} + \sin\frac{C}{2}}$

     $\Rightarrow \cosec\frac{A}{2} + \cosec\frac{B}{2} + \cosec\frac{C}{2} \geq 6$

237. $\cos A + \cos B + \cos C -\frac{3}{2} = 2\cos\frac{A + B}{2}\cos\frac{A - B}{2} + 1 - 2\sin^2\frac{C}{2} - \frac{3}{2}$

     $\Rightarrow -2\sin^2\frac{C}{2} + 2\cos\frac{A - B}{2}\sin\frac{C}{2} - \frac{1}{2} = 0$

     Clearly $D = 4\cos^2\frac{A - B}{2} - 4 < 0$ so sign of quadratic equation will be same as that of first term.

     $\Rightarrow \cos A + \cos B + \cos C \leq \frac{3}{2}$

     Now $\cos A + \cos B + \cos C - 1 = 2\sin\frac{C}{2}\cos\frac{A - B}{2} - 2\sin^\frac{C}{2}$

     $= 2\sin\frac{C}{2}\left[\cos\frac{A - B}{2} - \cos\frac{A + B}{2}\right]$

     $= 4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2} > 0$

     $\therefore \cos A + \cos B + \cos C > 1$

238. $y=2\cos A\cos B\cos C=[\cos(A-B)+\cos(A+B)]\cos C=[\cos(A-B)-\cos C]\cos C$

     $\implies\cos^2C-\cos(A-B)\cos C+y=0$

     which is quadratic equation in $\cos C$ which would be real.

     $\Rightarrow D \geq 0 \implies \cos^2(A-B)-4y\ge0\iff y\le\dfrac{\cos^2(A-B)}4\le\dfrac14$

     Hence proved.

239. Let $A$ be the center of first circle having radius $a$ and $B$ be the center of second circle having radius $b.$

     Let the two circles intersect at $C$ and $D$ so $\angle ACB = \angle ADB = \theta$

     We know that perpendicular from the center of a circle divides the chord in two equal parts. So $AB$ will divide $CD$ in two equal parts.

     Let $CD = 2x.$ Let $AB$ cut $CD$ at $O$ then $OC = OD = x$

     $AB = OA + OB = \sqrt{a^2 - x^2} + \sqrt{b^2 - x^2}$

     Clearly, $\angle ACB = \theta$

     Applying cosine law in $\triangle ABC$

     $AB^2 = AC^2 + BC^2 - 2.AC.BC\cos(\pi - \theta)$

     $\Rightarrow a^2 - x^2 + b^2 - x^2 + 2\sqrt{a^2 - x^2}\sqrt{b^2 - x^2} = a^2 + b^2 + 2ab\cos\theta$

     $\Rightarrow CD = 2x = \frac{2ab\sin\theta}{\sqrt{a^2 + b^2 + 2ab\cos\theta}}$

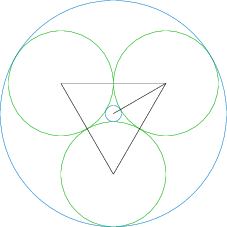
240. The diagram is given below:

     

     Let the triangle be $ABC$ which will be equilateral triangle having radius $2$ if all the circles are unit circle(i.e. having radius $1$ ).

     There will be two circles which will touch all three circles. One is the smaller one which will be inside the area enclosed by three circles and the other will be one which will enclose all the circles.

     Clearly, the center of the two circles will bisect the angles of the triangle.

     $\therefore \cos30^\circ = \frac{1}{x + 1}$ where $x$ is the radius of inner circle.

     $\implies x = \frac{2 - \sqrt{3}}{\sqrt{3}}$

     Radius of outer circle $= 2 + x = \frac{2 + \sqrt{3}}{\sqrt{3}}$

241. We have to prove that $\sum_{r=0}^n{}^nC_ra^rb^{n - r}\cos[rB - (n - r)A] = C^n$

     From De Movire’s theorem(this we have not studied yet),

     L.H.S. $= \sum_{r = 0}^n(ae^{iB})^r(b.e^{-iA})^r$

     $= (ae^iB + be^{-iA})^n = (a\cos B + ia\sin B + b\cos A - ib\sin A)$

     $\left[\because \frac{a}{\sin A} = \frac{b}{\sin B}\right]$

     $= (a\cos B + b\cos A)^n = c^n$

242. Let $A = B \implies A + B + C = \pi \implies 2A + C = \pi$

     Given, $\tan A +\tan B + \tan C = k$

     $\implies 2\tan A + \tan(\pi - 2A) = k$

     $\implies 2\tan A\left(1 + \frac{1}{1 - \tan^2A}\right) = k$

     $\implies 2\tan A\frac{\tan^2A}{1 - \tan^2A} = k$

     $\implies \frac{2\tan^3A}{1 - \tan^2A} = k$

     Now, since it is an isoscles triangle $A < \pi/2$

     So there are three possibilities, $0 < A < \pi/4, A=\pi/4, \pi/4 < A < \pi/2$

     In first case $k < 0,$ in second case $k=\infty$ and in third case $k > 0$

     Whenever $k<0$ or $k>0$ multiple isosceles triangles are possible. For example, for $k < 0$ i.e. for $0 < A < \pi/4, A$ can assume values like $\pi/6, \pi/5, \pi/7$ and so on.

     Similarly, for $k > 0, A$ can assume multiple values.

     However, if $k = \infty$ then $A, B$ can have only one value i.e. $\pi/4$ and only one isoceles triangle is possible.

243. We have to prove that $\Delta \leq \frac{s^2}{3\sqrt{3}}$

     i.e. $s(s - a)(s - b)(s - c) \leq \frac{s^4}{27}$

     $\implies \frac{(s - a)(s - b)(s - c)}{s^3}\leq 27$

     We know that A.M. $\geq$ G.M.

     $\implies \frac{s - a + s - b + s - c}{3s}\geq \sqrt[3]{\frac{(s - a)(s - b)(s - c)}{s^3}}$

     $\implies \frac{1}{3}\geq \sqrt[3]{\frac{(s - a)(s - b)(s - c)}{s^3}}$

     Cubing we get,

     $\frac{(s - a)(s - b)(s - c)}{s^3}\leq 27$

     Hence proved.

244. Let $a=3x+4y,b=4x+3y$ and $c=5x+5y$ be the largest side.

     $\cos C = \frac{a^2 + b^2 - c^2}{2ab} = \frac{-2xy}{2(3x + 4y)(4x + 3y)} < 0~\forall x, y >0$

     Thus, it is an obstuse angled triangle.

245. $\Delta = \frac{1}{2}ah_1 = \frac{1}{2}bh_2 = \frac{1}{2}ch_3$

     $\implies h_1 = \frac{2\Delta}{a}, h_2 = \frac{2\Delta}{b}, h_3 = \frac{2\Delta}{h_3}$

     We know that $r = \frac{\Delta}{s}$

     Now it is trivial to show the required condition.

246. $\Delta_0$ can be evaluated to be $\frac{1}{2}\frac{rS}{R}$

     Likewise $\Delta_1 = \frac{1}{2}\frac{r_1S}{R}$ and so on.

     Now it is trivial to prove the required equality.