Let a=8 cm, b=10 cm and c=12 cm. So the smallest angle will be A and greatest angle will
be C. So from cosine rule,
cosA=2bcb2+c2−a2=2.10.12100+144−64=43
cosC=2aba2+b2−c2=2.8.1064+100−144=81
cos2A=2cos2A−1=2.169−1=81=cosC
Thus, we see that greatest angle is double to that of smallest angle.
Let 11b+c=12c+a=13a+b,=k
∴b+c=11k,c+a=12k,a+b=13k⇒a+b+c=18k
∴a=7k,b=6k,c=5k
7cosA=2bcb2+c2−a2=2.6.7.7k236k2+25k2−49k2=351
19cosB=2cac2+a2−b2=2.5.7.19.k225k2+49k2−36k2=351
25cosC=2aba2+b2−c2=2.7.6.25.k249k2+36k2−25k2=351
Given, Δ=a2−(b−c)2⇒Δ=a2−b2−c2+2bc
⇒b2+c2−a2=2bc−Δ⇒2bccosA=2bc−21bcsinA
⇒4cosA+sinA=4⇒4(1−2sin22A)+2sin2Acos2A=4
2sin2A(cos2A−4sin2A)=0
⇒ either sin2A=0 or cos2A−4sin2A=0
A=0 is not possible. ∴tan2A=41
tanA=1−tan22A2tan2A=158.
Since A,B,C are in A.P. ∴2B=A+C
∵A+B+C=180∘⇒B=60∘
cosB=2cac2+a2−b2⇒21=2acc2+a2−b2⇒a2−ac+c2=b2
⇒a2−ac+a2a+c=ba+c
=ksinBk(sinA+sinC)=sinB2sin2A+Ccos2A−C
=sinB2sinBcos2A−C=2cos2A−C
Δ=21.a.p1∴p11=Δa
Similarly, p21=Δb,p31=Δc
L.H.S. =2Δa+b−c=2Δ(a+b+c)(a+b)2−c2
=2Δ(a+b+c)2ab+a2+b2−c2=2Δ(a+b+c)2ab+2abcosC
=Δ(a+b+c)ab(1+cosC)=Δ(a+b+c)2abcos22C
∵:tanθ=a−b2absin2C
⇒(a−b)2tan2θ=4absin22C⇒(a−b)2(sec2θ−1)=4absin22C
(a−b)2sec2θ=a2b2−2ab(1−2sin22C)
(a−b)2sec2θ=a2+b2−2abcosC=c2[∵cosC=2aba2+b2−c2]
⇒c=(a−b)secθ.
ΔABC=21bcsinA=216.3.sinC=9sinC
tan22A−B=1+cos(A−B)1−cos(A−B)=91
tan2A−B=±31
∵0<2A−B<90∘∴tan2A−B=31
tan2A−B=a+ba−bcot2C⇒cot2C=1
⇒C=90∘
Thus, required area =8sin90∘=9
The diagram is given below:
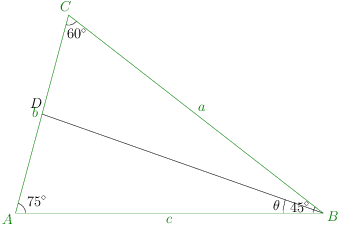
From question, ∠A=75∘,∠C=60∘⇒∠B=45∘
Also given, ΔBCDΔBAD=3=a.x.sin(45∘−θ)c.x.sinθ where
BD=x
⇒asin(45∘−θ)csinθ=3
⇒sinAsin(45∘−θ)sinCsinθ=3
⇒223+1sin(45∘−θ)23sinθ=3
⇒2sinθ=(3+1)sin(45∘−θ)
⇒2sinθ=(3+1)(21cosθ−21sinθ)
⇒2sinθ=(3+1)(cosθ−sinθ)
tanθ=31⇒θ=30∘
We find the largest angle which is opposite to side 7, if any angle can be obtuse angle then this one can.
cosθ=2.3.532+52−72=−3015=−21
⇒θ=120∘
Given ∠A=45∘,∠B=75∘⇒∠=60∘
We know that sinAa=sinBb=sinCc=k
a=21k,b=223+1k,c=23k
a+c2=21k+23k=21+3k
2b=23+1
⇒a+2c=2b
The diagram is given below:
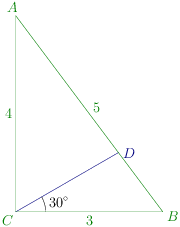
ΔBCD+ΔACD=ΔABC
⇒213CDsin30∘+214CDsin60∘=213.4
43CD+3CD=6⇒CD=3+4324
The smallest angle will be opposite to smallest side i.e. 4 cm. Similarly, greatest angle will be opposite to greatest
side i.e. 6 cm.
Let a=4 cm, b=5 cm and c=6 cm. Also, let opposite angles are A,B and C.
cosA=2bcb2+c2−a2=6045=43
cosC=2aba2+b2−c2=405=81
cos2A=2cos2A−1=2.169−1=81=cosC
The diagram is given below:

∠A+∠B+∠C=180∘=10∠B+∠B+∠B⇒∠B=15∘
⇒∠A=150∘
Let AB=AC=x
∴cos150∘=2.x.xx2+x2−a2
⇒−3x2=2x2−a2⇒x=2+31a
Let angles are A=2k,B=3k,C=7k∴2k+3k+7k=180∘⇒k=15∘
sinAa=sinBb=sinCc=l
sinA=21,sinB=21,sinC=22+3
Now the ratios of sides can be proven.
Clearly, the sides are in the ratio of 7:6:5
∴cosA=2.6.562+52−72=51
cosB=2.7.572+52−62=3519
cosC=2.7.672+62−52=75
∴cosA:cosB:cosC=7:19;25
tan2C=tan2π−(A+B)=cot2A+B=tan2A+tan2B1−tan2Atan2B
=65+37201−65.3720
=222305222122=305122=52
sinA=1+tan22A2tan2A=1+36252.65
=6160
sinB=1+tan22B2tan2B=1+13694002.3720
=17691480
sinB=1+tan22C2tan2C=1+254252
=2920
a+c=k(sinA+sinC)[sinAa=sinBb=sinCc=k]
=k(6160+2920)=17691740+1220=17692960=2b.
It is much easier to prove this problem in reverse.
Given, a+c1+b+c1=a+b+c3
Upon solving a2+b2−c2=ab
⇒2aba2+b2−c2=21=cos60∘=cosC
Let the sides be a,b,c. We know that Δ=21a.α because area = 21× base × altitude
Δ=21α⇒α=a2Δ⇒α1=2Δa
α21+β21+γ21=4Δ2a2+b2+c2
ΔcotA+cotB+cotC=ΔsinAcosA+ΔsinBcosB+ΔsinCcosC
Δ=21bcsinA⇒sinA=bc2Δ
∴ΔsinAcosA=2Δ2bccosA=4Δ2b2+c2−a2
∴ΔsinAcosA+ΔsinBcosB+ΔsinCcosC=4Δ2a2+b2+c2
Hence proven.
Given, ba=2+3=tan75∘=cos75∘sin75∘
sinBsinA=sin(75∘−15∘)sin(90∘+15∘)
⇒A=105∘,B=15∘ which satisfied A+B+C=180∘
cosC=21=2aba2+b2−c2⇒(1+32)+4−c2=2(1+3)
⇒c2=6⇒c=6
cosA=2bcb2+c2−a2=464+6−(1+3)2
=66+23=6+2⇒A=75∘
Thus, ∠B=45∘
Greatest angle will be opposite to greatest side i.e. x2+xy+y2
cosθ=2.x.yx2+y2−x2−xy−y2=−21⇒θ=120∘
Given sides are 2x+3,x2+3x+3 and x2+2x. Since lengths of sides is a positive quantity, therefore
x2+2x>0⇒x>0
This leads to the fact that x2+3x+3 will be greatest side.
cosθ=2(2x+3)(x2+2x)(2x+3)2+(x2+2x)2−(x2+3x+3)2
=4x3+14x2+12x4x2+12x+9+x4+4x3+4x2−x4−9x2−9−6x3−6x2−18x
=2(2x3+7x2+6x)−2x3−7x2−6x=−21=cos120∘
Given, 3a=b+c. We know that s=2a+b+c⇒s=2a
cot2Bcot2C=Δs(s−b).Δs(s−c)
=s(s−a)(s−b)(s−c)s2(s−b)(s−c)=s−as=2
We have to prove that asin(2A+B)=(b+c)sin2A
ab+c=sinAk(sinB+sinC)
=2sin3Acos2A2sin2B+ccos2B−C
=sin2Acos(2B−2C)
=cos[2B−{2π−(2A+B)}]sin2A
=sin2Asin(2A+B)
Numerator of L.H.S. =Δs(s−a)+Δs(s−b)+Δs(s−c)
=Δs(s−a+s−b+s−c)=Δs2=4Δ(a+b+c)2
Denominator of R.H.S. =sinAcosA+sinBcosB+sinCcosC
=2bcsinAb2+c2−a2+2casinBc2+a2−b2+2absinCa2+b2−c2
[ Δ=21bcsinA=21casinB=21absinC ]
=4Δa2+b2+c2
L.H.S. =a2+b2+c2(a+b+c)2
First term of L.H.S. =a2b2−c2sin2A=a2b2−c22sinAcosA
=a2b2−c2.2Ka.2bcb2+c2−a2
=Kabc1[(b2−c2)(b2+c2−a2)]=Kabc1[b4−c4−a2(b2−c2)]
Similarly, second term =Kabc1[c4−a4−b2(c2−a2)]
First term of L.H.S =a3cos(B−C)=a2[acos(B−C)]
=Ra2[2sinAcos(B−C)]=Ra2[2sin(B+C)cos(B−C)]=Ra2[sin2B+sin2C]
=Ra2[2sinBcosB+2sinCcosC]=a2[bcosB+ccosC]
Similarly, second term =b2[acosA+ccosC]
and third term =c2[acosA+bcosB]
Adding, ab[acosB+bcosA]+ca[ccosA+acosC]+bc[bcosC+ccosB]
=3abc= R.H.S.
L.H.S. =K2[sinB+sinC]2cos22B−C+K2[sinB−sinC]2sin22B−C
=K21(4sin22B+Ccos22B−Ccos22B−C+4cos22B+Csin22B−Csin2B−C)
=4k21(sin22B+C1+cos22B+C1)
=4K21(cos22A1+sin22A1)
=k21.4sin22Acos22A1=a21
First term of L.H.S. =cosBcosCa=cosBcosC2RsinA
=cosBcosC2Rsin(B+C)=2R(tanB+tanC)
Similarly, second term =2R(tanC+tanA) and third term =2R(tanA+tanB)
L.H.S. =4R[tanA+tanB+tanC]
=4R.tanAtanBtanC[∵A+B+C=π∴tanA+tanB+tanC=tanAtanBtanC]
=2.atanBtanCsecA= R.H.S.
We have to prove that (b−c)cos2A=asin2B−C
ab−c=sinAsinB−sinC=2sin2Acos2A2cos2B+Csin2B−C
=2sin2Acos2A2sin2Asin2B−C=cos3Asin2B−C
We have to prove that tan(2A+B)=c−bc+btan2A
c−bc+b=sinC−sinBsinC+sinB
=2cos2B+Csin2C−B2sin2B+Ccos2C−B
=tan2C−Btan2B+C=tan2π−B−A−Bcot2A
=tan3Atan(2A+B)
We have to prove that tan2A−B=a+ba−bcot2C
a+ba−b=sinA+sinBsinA−sinB=2sin2A+Bcos2A−B2cos2A+Bsin2A−B
=tan2A+Btan2A−B=cot2Ctan2A−B
L.H.S. =(b+c)cosA+(c+a)cosB+(a+b)cosC
=(acosB+bcosA)+(bcosC+ccosB)+(acosC+ccosA)
=c+a+b= R.H.S.
First term of L.H.S. =b+ccos2B−cos2C=k1[sinB+sinC(cosB+cosC)(cosB−cosC)]
=k1[2sin2B+Ccos3B−C2cos2B+Ccos2B−C.2sin2B+Csin2C−B]
=k1[2cos2B+Csin2C−B]=k1[sinC−sinB]
Similarly, second term =k1[sinA−sinC] and third term =k1[sinB−sinA]
Thus, L.H.S. = R.H.S. = 0
First term of L.H.S. =a3sin(B−C)=Ra2.2sinAsin(B−C)=Ra2.2sin(B+C)sin(B−C)
=Ra2[cos2C−cos2B]=Ra2(1−sin2C−1+sin2B)=R[(2RsinB)2−(2RsinC)2]
=R[b2−c2]
Similarly, second term =R[c2−a2] and third term =R[a2−b2]
Thus, L.H.S. =0= R.H.S.
Consider first term i.e. (b+c−a)tan2A
b+c−a=2s−2a=2(s−a)
tan2A=s(s−a)(s−b)(s−c)
∴(b+c−a)tan2A=2s(s−a)(s−b)(s−a)
Similarly, (c+a−b)tan2B=2s(s−a)(s−b)(s−a)=(a+b−c)tan2C
1−tan2Atan2B=1=−s(s−a)(s−b)(s−c).s(s−b)(s−a)(s−c)
=1−ss−c=sc=a+b+c2c= R.H.S.
L.H.S. =a2cos2A−b2cos2B
=a21−2sin2A−b21−2sin2B
=a21−2.4r2a2−b21−2.4r2b2
=a21−b21= R.H.S.
We have to prove that a2(cos2B−cos2C)+b2(cos2C−cos2A)+c2(cos2A−cos2B)=0
L.H.S. =a2(sin2C−sin2B)+b2(sin2A−sin2C)+c2(sin2B−sin2A)
=4R2sinA(sin2C−sin2B)+4R2sin2B(sin2A−sin2C)+4R2sin2C(sin2B−sin2A)
=0= R.H.S.
First term of L.H.S. =sinB+sinCa2sin(B−C)
=sinB+sinC2RasinAsin(B−C)=sinB+sinC2Rasin(B+C)sin(B−C)
=sinB+sinCRa(cos2C−cos2B)=sinB+sinCRa(2sin2B−2sin2C)
=2Ra(sinB−sinC)=a(b−c)
Similarly, second term =b(c−a) and third term =c(a−b)
Thus, L.H.S. =0= R.H.S.
L.H.S. =acosA+bcosB+ccosC
=2abcb2+c2−a2+2abcc2+a2−b2+2abca2+b2−c2
=2abca2+b2+c2= R.H.S.
First term of L.H.S. =acosA+bca
=2abcb2+c2−a2+bca=2abca2+b2+c2
Similarly, second term = third term = 2abca2+b2+c2
First term of L.H.S. =(b2−c2)sinAcosA
=2abc(b2−c2)(b2+c2−a2)=2abcb4−c4−a2(b2−c2)
Similarly, second term =2abcc4−a4−b2(c2−a2)
and third term =2abca4−b4−c2(a2−b2)
Thus, L.H.S. =0= R.H.S.
L.H.S. =(b−c)Δs(s−a)+(c−a)Δs(s−b)+(a−b)Δs(s−c)
=Δs(b2−c2+c2−a2+a2−b2)=0= R.H.S.
L.H.S. =(a−b)2+sin22C[(a+b)2−(a−b)2]
=(a−b)2+2ab.2sin22C=(a−b)2+2ab[1−cosC]
=a2−2ab+b2+2ab−a2−b2+c2=c2= R.H.S.
L.H.S. =a+ba−b=sinA+sinBsinA−sinB
=2sin2A=Bcos2A−B2cos2A+Bsin2A−B
=cot2A+Btan2A−B= R.H.S.
The diagram is given below:
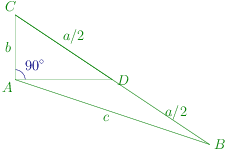
cosC=a/2b=a2b
2aba2+b2−c2=a2b⇒3b2=a2−c2
cosAcosC=2bcb2+c2−a2.a2b
=ac3a2−c2+c2−a2=3ac2(c2−a2)= R.H.S.
The diagram is given below:
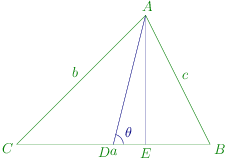
Here BD=DC. Let AE⊥BC
Now, AC2−AB2=(AE2+EC2)−(AE2+BE2)
=EC2−BE2=(EC+BE)(EC−BE)=BE[(ED+DC)−(BD−ED)]
=2BE.ED[∵BD=DC]
Also, 4Δ=4.21BC.AE=2BC.AE
4ΔAC2−AB2=2BC.AE2BE.ED=AEED=cotθ
The diagram is given below:
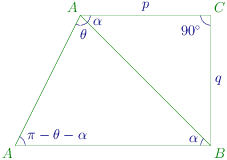
Let ∠DBA=α then
∠BDC=α[∵AB∥DC]
⇒∠DAB=π−(θ+α)
Now applying sine rule in △ADB
sinθAB=sin(π−θ−α)p2+q2
AB=sin(θ+α)p2+q2sinθ
=sinθcosα+sinαcosθp2+q2sinθ
=pcosθ+qsinθ(p2+q2)sinθ
The diagram is given below:
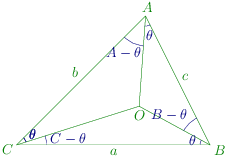
∠AOB=π−B and ∠BOC=π−C
Applying sine rule in triangle AOB, we have
sinθOB=sin(π−B)c∴OB=sinBcsinθ
Similarly, in triangle BOC,
OB=sinCasin(C−θ)
⇒sinB2RsinCsinθ=sinC2RsinAsin(C−θ)
sinAsinBsinC=sinCsinθsin(C−θ)
sinAsinBsin(A+B)=sinCsinθsinCcosθ−cosCsinθ
cotB+cotA=cotθ−cotC
cotθ=cotA+cotB+cotC






