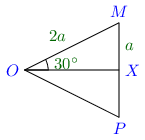6. Trigonometrical Ratios of Angle and Sign#

6.1. Values of Trigonometrical Ratios for Some Useful Angles#

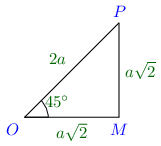
6.1.1. Angle of 45∘45^\circ#

45 degree angle

Consider the above figure, which is a right-angle triangle, drawn so that ∠OMP=90∘\angle OMP = 90^\circ and ∠MOP=45∘.\angle MOP = 45^\circ. We know that sum of all angles of a triangle is equal to 180∘.180^\circ. Thus,

∠OPM=180∘−∠MOP−∠OMP=180∘−90∘−45∘=45∘\angle OPM = 180^\circ - \angle MOP - \angle OMP = 180^\circ - 90^\circ - 45^\circ = 45^\circ

∴OM=MP.\therefore OM = MP. Let OP=2a,OP = 2a, then from Pythogoras theorem, we can write

4a2=OP2=OM2+MP2=2.OM2⇒OM=a2=MP4a^2 = OP^2 = OM^2 + MP^2 = 2.OM^2\Rightarrow OM = a\sqrt{2} = MP

sin⁡45∘=MPOP=a22a=12\sin 45^\circ = \frac{MP}{OP} = \frac{a\sqrt{2}}{2a} = \frac{1}{\sqrt{2}}

Other trigonometric ratios can be deduced easily from this.

6.1.2. Angle of 30∘30^\circ and 50∘50^\circ#

30 degree angle

Consider an equilateral △OMP\triangle OMP. Let the sides OM,OP,MPOM, OP, MP be each 2a2a. We draw a bisector of ∠MOP\angle MOP which will be a perpendicular bisector of MPMP at XX because the triangle is equilateral. Thus, MX=a.MX = a. Thus, in △OMX,OM=2a,MX=a,∠MOX=30∘,∠OXM=90∘\triangle OMX, OM = 2a, MX = a, \angle MOX = 30^\circ, \angle OXM = 90^\circ because each angle is 60∘60^\circ in an equilateral triangle.

sin⁡MOX=MXOM=12⇒sin⁡30∘=12\sin MOX = \frac{MX}{OM} = \frac{1}{2} \Rightarrow \sin 30^\circ = \frac{1}{2}

Similarly, ∠OMX=60∘\angle OMX = 60^\circ because sum of all angles of a triangle is 180∘180^\circ

cos⁡OMX=MXOM=12⇒cos⁡60∘=12\cos OMX = \frac{MX}{OM} = \frac{1}{2}\Rightarrow \cos 60^\circ = \frac{1}{2}

All other trigonometric ratios for these can be foun from these two.

6.1.3. Angle of 0∘0^\circ#

0 degree angle

Consider the △MOP\triangle MOP such that the side MP is smaller than any quantiry we can assign i.e. what we denote by 0. Thus, ∠MOP\angle MOP is what is called approaching 00 or lim⁡x→0\lim_{x \to 0} in terms of Calculus. Why we have to take such a value is because if any anngle of a triangle is equal to 0∘0^\circ then the triagle won’t exist. Thus these values are limiting values as you will learn in Calculus.

However, in this case sin⁡0∘=MPOP=0OP=0.\sin 0^\circ = \frac{MP}{OP} = \frac{0}{OP} = 0. Now other trigonometric ratios can be found with ease.

6.1.4. Angle of 90∘90^\circ#

In the previous figure as ∠OMP\angle OMP will approach 0∘,0^\circ, the ∠OPM\angle OPM will approach 90∘.90^\circ. Also, OPOP will approach the length of OM.OM. Similar to previos case in right-angle triangle if one angle(other than right angle) approaches 0∘0^\circ the other one will approach 90∘90^\circ and at that value the triangle will cease to exist.

Thus, sin⁡90∘=OMOP=OPOP=1.\sin 90^\circ = \frac{OM}{OP} = \frac{OP}{OP} = 1. Now it is trivial to find other trigonometric ratios.

Given below is a table of most useful angles:

Values of useful angles#

Angle

0∘0^\circ

30∘30^\circ

45∘45^\circ

60∘60^\circ

90∘90^\circ

sin⁡\sin

00

12\frac{1}{2}

12\frac{1}{\sqrt{2}}

32\frac{\sqrt{3}}{2}

11

cos⁡\cos

11

32\frac{\sqrt{3}}{2}

12\frac{1}{\sqrt{2}}

12\frac{1}{\sqrt{2}}

00

tan⁡\tan

00

13\frac{1}{\sqrt{3}}

11

3\sqrt{3}

∞\infty

cosec⁡\cosec

∞\infty

22

2\sqrt{2}

23\frac{2}{\sqrt{3}}

11

sec⁡\sec

11

23\frac{2}{\sqrt{3}}

2\sqrt{2}

22

∞\infty

cot⁡\cot

∞\infty

3\sqrt{3}

11

13\frac{1}{\sqrt{3}}

00

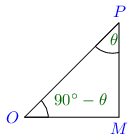
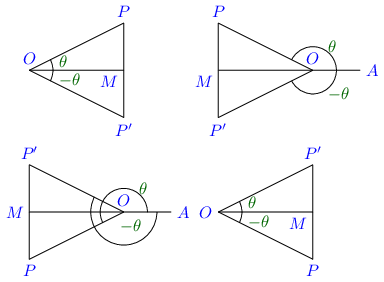
6.2. Complementary Angles#

complementary angles

Angles are said to be complementary if their sum is equal to one right angle i.e 90∘.90^\circ. Thus, if measure of one angle is θ\theta the other will automatically be 90∘−θ.90^\circ - \theta.

Consider the above figure. △OMP\triangle OMP is a right-angle triangle whose ∠OMP\angle OMP is a right angle. Since the sum of all angles is equal to 180∘,180^\circ, therefore sum of ∠MOP\angle MOP and ∠MPO\angle MPO will be equal to one right angle or 90∘90^\circ i.e. they are complementatry angles.

Let ∠MOP=θ\angle MOP = \theta then ∠MPO=90∘−θ.\angle MPO = 90^\circ - \theta. When ∠MPO\angle MPO is considered MPMP becomes the base and OMOM becomes the perpendicular.

Thus, sin⁡(90∘−θ)=sin⁡MPO=MOPO=cos⁡MOP=cos⁡θ\sin(90^\circ - \theta) = \sin MPO = \frac{MO}{PO} = \cos MOP = \cos \theta

cos⁡(90∘−θ)=sin⁡MPO=PMPM=sin⁡MOP=sin⁡θ\cos(90^\circ - \theta) = \sin MPO = \frac{PM}{PM} = \sin MOP = \sin \theta

tan⁡(90∘−θ)=tan⁡MPO=OMMP=cot⁡MOP=cot⁡θ\tan(90^\circ - \theta) = \tan MPO = \frac{OM}{MP} = \cot MOP = \cot \theta

Similarly, cot⁡(90∘−θ)=tan⁡θ\cot(90^\circ - \theta) = \tan \theta

cosec⁡(90∘−θ)=sec⁡θ\cosec(90^\circ - \theta) = \sec \theta

sec⁡(90∘−θ)=cosec⁡θ\sec(90^\circ - \theta) = \cosec \theta

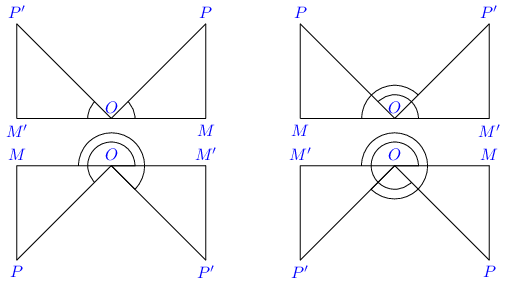
6.3. Supplementary Angles#

supplemntary angles

Angles are said to be supplementary if their sum is equal to two right angles i.e. 180∘.180^\circ. Thus, if measure of one angle is θ\theta and oher will automaticaly be 180∘−θ.180^\circ - \theta.

Conside the above figure which include the angles of 180∘+θ.180^\circ + \theta. In each figure OMOM and OM′OM' are drawn in different directions, while MPMP and M′P′M'P' are drawn in the same direction, so that

OM′=−OMOM' = -OM and M′P′=MPM'P' = MP

Hencem we can say that

sin⁡(180∘−θ)=sin⁡MOP′=M′P′OP′=MPOP=sin⁡θ\sin(180^\circ - \theta) = \sin MOP' = \frac{M'P'}{OP'} = \frac{MP}{OP} = \sin \theta

cos⁡(180∘−θ)=cos⁡MOP′=OM′OP′=−OMOP=−cos⁡θ\cos(180^\circ - \theta) = \cos MOP' = \frac{OM'}{OP'} = \frac{-OM}{OP} = -\cos \theta

tan⁡(180∘−θ)=tan⁡MOP′=OM′M′P′=−OMMP=−tan⁡θ\tan(180^\circ - \theta) = \tan MOP' = \frac{OM'}{M'P'} = \frac{-OM}{MP} = -\tan \theta

Similarly, cot⁡(180∘−θ)=−cot⁡θ\cot(180^\circ - \theta) = -\cot \theta

sec⁡(180∘−θ)=−sec⁡θ\sec(180^\circ - \theta) = -\sec \theta

cosec⁡(180∘−θ)=cosec⁡θ\cosec(180^\circ - \theta) = \cosec \theta

6.4. Angles of −θ-\theta#

negative angled

Consider the above diagram which plots angles of θ\theta and −θ.-\theta. Note that MPMP and MP′MP' are equal in magnitude but are opposite in sign. Thus, we have

sin⁡(−θ)=MP′OP′=−MPOP=−sin⁡θ\sin(-\theta) = \frac{MP'}{OP'} = \frac{-MP}{OP} = -\sin\theta

cos⁡(−θ)=OMMP′=OMOP=cos⁡θ\cos(-\theta) = \frac{OM}{MP'} = \frac{OM}{OP} = \cos\theta

tan⁡(−θ)=MP′OM=−MPOM=−tan⁡θ\tan(-\theta) = \frac{MP'}{OM} = \frac{-MP}{OM} = -\tan\theta

Similalry, cot⁡(−θ)=−cot⁡θ\cot(-\theta) = -\cot\theta

sec⁡(−θ)=sec⁡θ\sec(-\theta) = \sec\theta

cosec⁡(−θ)=−cosec⁡θ\cosec(-\theta) = -\cosec\theta

6.5. Angles of 90∘−θ90^\circ -\theta and 90∘+θ90^\circ+\theta#

Similarly it can be proven that(diagram has been left as an exercise)

sin⁡(90∘−θ)=cos⁡θ\sin(90^\circ -\theta) = \cos\theta

cos⁡(90∘−θ)=sin⁡θ\cos(90^\circ -\theta) = \sin\theta

tan⁡(90∘−θ)=cot⁡θ\tan(90^\circ -\theta) = \cot\theta

cot⁡(90∘−θ)=tan⁡θ\cot(90^\circ -\theta) = \tan\theta

sec⁡(90∘−θ)=cosec⁡θ\sec(90^\circ -\theta) = \cosec\theta

cosec⁡(90∘−θ)=sec⁡θ\cosec(90^\circ -\theta) = \sec\theta

sin⁡(90∘+θ)=cos⁡θ\sin(90^\circ+\theta) = \cos\theta

cos⁡(90∘+θ)=−sin⁡θ\cos(90^\circ+\theta) = -\sin\theta

tan⁡(90∘+θ)=−cot⁡θ\tan(90^\circ+\theta) = -\cot\theta

cot⁡(90∘+θ)=−tan⁡θ\cot(90^\circ+\theta) = -\tan\theta

sec⁡(90∘+θ)=−cosec⁡θ\sec(90^\circ+\theta) = -\cosec\theta

cosec⁡(90∘+θ)=sec⁡θ\cosec(90^\circ+\theta) = \sec\theta

6.6. Angles of 180∘+θ180^\circ + \theta#

Angles of 180∘+θ,270∘−θ,270∘+theta180^\circ + \theta, 270^\circ -\theta, 270^\circ + theta can be found by using previous relations. For example,

sin⁡(180+θ)=sin⁡(90+90+θ)=cos⁡(90+θ)=−sin⁡θ\sin(180 + \theta) = \sin(90 + 90 + \theta) = \cos(90 + \theta) = -\sin\theta

cos⁡(180+θ)=cos⁡(90+90+θ)=−sin⁡(90+θ)=−cos⁡θ\cos(180 + \theta) = \cos(90 + 90 + \theta) = -\sin(90 + \theta) = -\cos\theta

tan⁡(180+θ)=tan⁡(90+90+θ)=−cos⁡(90+θ)=tan⁡θ\tan(180 + \theta) = \tan(90 + 90 + \theta) = -\cos(90 + \theta) = \tan\theta

Similarly, cot⁡(180+θ)=cot⁡θ\cot(180 + \theta) = \cot\theta

sec⁡(180+θ)=−sec⁡θ\sec(180 + \theta) = -\sec\theta

cosec⁡(180+θ)=−cosec⁡θ\cosec(180 + \theta) = -\cosec\theta

6.7. Angles of 360∘+θ360^\circ + \theta#

For angles of θ\theta the radius vector makes an angle of θ\theta with initial side. For angles of 360∘+θ360^\circ + \theta it will complete a full revolution and then make an angle of θ\theta with initial side. Thus, the trigonometrical ratios for an angle of 360∘+θ360^\circ + \theta are the same as those for θ.\theta.

It is clear that angle will remain θ\theta for any multiple of 360∘.360^\circ.

6.8. Problems#

  1. If A=30∘,A = 30^\circ, verify that

    1. cos⁡2A=cos⁡2A−sin⁡2A=2cos⁡2A−1\cos 2A = \cos^2A - \sin^2A = 2\cos^2A - 1

    2. sin⁡2A=2sin⁡Acos⁡A\sin 2A = 2\sin A\cos A

    3. cos⁡3A=4cos⁡3A−3cos⁡A\cos 3A = 4\cos^3A - 3\cos A

    4. sin⁡3A=3sin⁡A−4sin⁡3A\sin 3A = 3\sin A - 4\sin^3A

    5. tan⁡2A=2tan⁡A1−tan⁡2A\tan 2A = \frac{2\tan A}{1 - \tan^2 A}

  2. If A=45∘,A = 45^\circ, verify that

    1. sin⁡2A=2sin⁡Acos⁡A\sin 2A = 2\sin A\cos A

    2. cos⁡2A=1−2sin⁡2A\cos 2A = 1 - 2\sin^2A

    3. tan⁡2A=2tan⁡A1−tan⁡2A\tan 2A = \frac{2\tan A}{1 - \tan^2A}

Verify that

  1. sin⁡230∘+sin⁡245∘+sin⁡260∘=32\sin^230^\circ + \sin^245^\circ + \sin^260^\circ = \frac{3}{2}

  2. tan⁡230∘+tan⁡245∘+tan⁡260∘=413\tan^230^\circ + \tan^245^\circ + \tan^260^\circ = 4\frac{1}{3}

  3. sin⁡30∘cos⁡60∘+sin⁡60∘cos⁡30∘=1\sin 30^\circ\cos 60^\circ + \sin 60^\circ\cos 30^\circ = 1

  4. cos⁡45∘cos⁡60∘−sin⁡45∘sin⁡60∘=−3−122\cos 45^\circ\cos 60^\circ - \sin 45^\circ\sin 60^\circ = -\frac{\sqrt{3} - 1}{2\sqrt{2}}

  5. cosec⁡245∘.sec⁡230∘.sin⁡290∘.cos⁡60∘=113\cosec^245^\circ.\sec^230^\circ.\sin^290^\circ.\cos 60^\circ = 1\frac{1}{3}

  6. 4cot⁡245∘−sec⁡260∘+sin⁡230∘=144\cot^245^\circ-\sec^260^\circ + \sin^230^\circ = \frac{1}{4}

Prove that

  1. sin⁡420∘cos⁡390∘+cos⁡(−300∘)sin⁡(−330∘)=1\sin 420^\circ\cos 390^\circ + \cos(-300^\circ)\sin(-330^\circ) = 1

  2. cos⁡570∘sin⁡510∘−sin⁡330∘cos⁡390∘=0\cos 570^\circ\sin 510^\circ -\sin 330^\circ\cos 390^\circ = 0

What are the values of cos⁡A−sin⁡A\cos A - \sin A and tan⁡A+cot⁡A\tan A + \cot A when A has the values

  1. π3\frac{\pi}{3}

  2. 2π3\frac{2\pi}{3}

  3. 5π4\frac{5\pi}{4}

  4. 7π4\frac{7\pi}{4}

  5. 11π3\frac{11\pi}{3}

What values between 0∘0^\circ and 360∘360^\circ may AA have when

  1. sin⁡A=12\sin A = \frac{1}{\sqrt{2}}

  2. cos⁡A=−12\cos A = -\frac{1}{2}

  3. tan⁡A=−1\tan A = -1

  4. cot⁡A=−3\cot A = -\sqrt{3}

  5. sec⁡A=−23\sec A = -\frac{2}{\sqrt{3}}

  6. cosec⁡A=−2\cosec A = -2

Express in terms of the ratios of a positive angle, which is less than 45∘,45^\circ, the quantities

  1. sin⁡(−65∘)\sin(-65^\circ)

  2. cos⁡(−84∘)\cos(-84^\circ)

  3. tan⁡137∘\tan 137^\circ

  4. sin⁡168∘\sin 168^\circ

  5. cos⁡287∘\cos 287^\circ

  6. tan⁡(−246∘)\tan(-246^\circ)

  7. sin⁡843∘\sin 843^\circ

  8. cos⁡(−928∘)\cos(-928^\circ)

  9. tan⁡1145∘\tan 1145^\circ

  10. cos⁡1410∘\cos 1410^\circ

  11. cot⁡(−1054∘)\cot(-1054^\circ)

  12. sec⁡1327∘\sec 1327^\circ

  13. cosec⁡(−756∘)\cosec (-756^\circ)

What sign has sin⁡A+cos⁡A\sin A + \cos A for the following values of AA?

  1. 140∘140^\circ

  2. 278∘278^\circ

  3. −356∘-356^\circ

  4. −1125∘-1125^\circ

What sign has sin⁡A−cos⁡A\sin A - \cos A for the following values of AA?

  1. 215∘215^\circ

  2. 825∘825^\circ

  3. −634∘-634^\circ

  4. −457∘-457^\circ

  5. Find the sine and cosine of all angles in the first four quadrants whose tangents are equal to cos⁡135∘.\cos 135^\circ.

Prove that

  1. sin⁡(270∘+A)=−cos⁡A\sin(270^\circ + A) = -\cos A and tan⁡(270∘+A)=−cot⁡A\tan(270^\circ + A) = -\cot A

  2. cos⁡(270∘−A)=−sin⁡A\cos(270^\circ - A) = -\sin A and cot⁡(270∘−A)=tan⁡A\cot(270^\circ - A) = \tan A

  3. cos⁡A+sin⁡(270∘+A)−sin⁡(270∘−A)+cos⁡(180∘+A)=0\cos A + \sin(270^\circ + A) - \sin(270^\circ - A) + \cos(180^\circ + A) = 0

  4. sec⁡(270∘−A)sec⁡(90∘−A)−tan⁡(270∘−A)tan⁡(90∘+A)+1=0\sec(270^\circ - A)\sec(90^\circ - A) - \tan(270^\circ - A)\tan(90^\circ + A) + 1 = 0

  5. cot⁡A+tan⁡(180∘+A)+tan⁡(90∘+A)+tan⁡(360∘−A)=0\cot A + \tan(180^\circ + A) + \tan(90^\circ + A) + \tan(360^\circ - A) = 0

  6. Find the value of 3tan⁡245∘−sin⁡260∘−12cot⁡230∘+18sec⁡245∘3\tan^245^\circ - \sin^260^\circ - \frac{1}{2}\cot^230^\circ + \frac{1}{8}\sec^245^\circ

  7. Simplify sin⁡300∘.tan⁡330∘.sec⁡420∘tan⁡135∘.sin⁡210∘.sec⁡315∘\frac{\sin 300^\circ.\tan 330^\circ.\sec 420^\circ}{\tan 135^\circ.\sin 210^\circ.\sec 315^\circ}

  8. Show that tan⁡1∘tan⁡2∘…tan⁡89∘=1\tan 1^\circ\tan 2^\circ \ldots \tan 89^\circ = 1

  9. Show that sin⁡25∘+sin⁡210∘+sin⁡215∘+…+sin⁡290∘=912\sin^25^\circ + \sin^210^\circ + \sin^215^\circ + \ldots + \sin^290^\circ = 9\frac{1}{2}

  10. Find the value of cos⁡2π16+cos⁡23π16+cos⁡25π16+cos⁡27π16\cos^2\frac{\pi}{16} + \cos^2\frac{3\pi}{16} + \cos^2\frac{5\pi}{16} + \cos^2\frac{7\pi}{16}

Find the value of the following:

  1. sec⁡2π6sec⁡2π4+tan⁡2π3sin⁡2π2\sec^2\frac{\pi}{6}\sec^2\frac{\pi}{4} + \tan^2\frac{\pi}{3}\sin^2\frac{\pi}{2}

  2. cot⁡230∘−2cos⁡260∘−34sin⁡245∘−4sin⁡230∘\cot^230^\circ - 2\cos^260^\circ - \frac{3}{4}\sin^245^\circ - 4\sin^230^\circ

  3. sec⁡480∘cosec⁡570∘.tan⁡330∘sin⁡600∘.cos⁡660∘.cot⁡405∘\frac{\sec 480^\circ\cosec 570^\circ.\tan 330^\circ}{\sin 600^\circ.\cos 660^\circ.\cot 405^\circ}

  4. If A=30∘,A = 30^\circ, show that cos⁡6A+sin⁡6A=1−sin⁡2Acos⁡2A\cos^6A + \sin^6A = 1 - \sin^2A\cos^2A

  5. Show that (tan⁡π4+cot⁡π4+sec⁡π4)(tan⁡π4+cot⁡π4−sec⁡π4)=cosec⁡2π4\left(\tan \frac{\pi}{4} + \cot \frac{\pi}{4} + \sec\frac{\pi}{4}\right)\left(\tan \frac{\pi}{4} + \cot \frac{\pi}{4} - \sec \frac{\pi}{4}\right) = \cosec^2 \frac{\pi}{4}

  6. Show that sin⁡26∘+sin⁡6212∘+sin⁡218∘+…+sin⁡284∘+sin⁡290∘=8\sin^26^\circ + \sin6^212^\circ + \sin^218^\circ + \ldots + \sin^284^\circ + \sin^290^\circ = 8

  7. Show that tan⁡9∘.tan⁡27∘.tan⁡45∘.tan⁡63∘.tan⁡81∘=1\tan 9^\circ.\tan 27^\circ.\tan 45^\circ.\tan 63^\circ.\tan 81^\circ = 1

  8. Show that ∑r=19sin⁡2rπ18=5\sum_{r = 1}^9 \sin^2\frac{r\pi}{18} = 5

  9. If 4nα=π,4n\alpha = \pi, show that tan⁡αtan⁡2αtan⁡3α.….tan⁡(2n−2)αtan⁡(2n−1)α=1\tan\alpha\tan2\alpha\tan3\alpha. \ldots .\tan(2n - 2)\alpha\tan(2n - 1)\alpha = 1