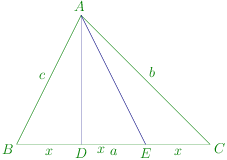
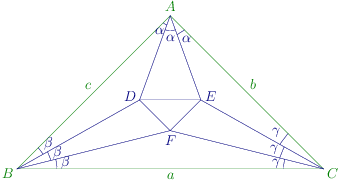
The diagram is given below:
Let B D = D E = E C = x . BD = DE = EC = x. B D = D E = EC = x .
∠ B A D = α , ∠ D A E = β , E A C = γ , C E A = θ \angle BAD = \alpha, \angle DAE = \beta, EAC = \gamma, CEA = \theta ∠ B A D = α , ∠ D A E = β , E A C = γ , CE A = θ
Given, tan α = t 1 , tan β = t 2 , tan γ = t 3 \tan\alpha = t_1, \tan\beta = t_2, \tan\gamma = t_3 tan α = t 1 , tan β = t 2 , tan γ = t 3
Applying m : n m:n m : n △ A B C , \triangle ABC, △ A BC ,
( 2 x + x ) cot θ = 2 x cot ( α + β ) − x cot γ (2x + x)\cot\theta = 2x\cot(\alpha + \beta) - x\cot\gamma ( 2 x + x ) cot θ = 2 x cot ( α + β ) − x cot γ
From △ A D C , \triangle ADC, △ A D C ,
2 x cot θ = x cot β − x cot γ 2x\cot\theta = x\cot\beta - x\cot\gamma 2 x cot θ = x cot β − x cot γ
⇒ 3 2 = 2 ( α + β ) − cot γ cot β − cot γ \Rightarrow \frac{3}{2} = \frac{2(\alpha + \beta) - \cot\gamma}{\cot\beta - \cot\gamma} ⇒ 2 3 = c o t β − c o t γ 2 ( α + β ) − c o t γ
⇒ 3 cot β − 3 cot γ = 4 cot ( α + β ) − 2 cot γ \Rightarrow 3\cot\beta - 3\cot\gamma = 4\cot(\alpha + \beta) - 2\cot\gamma ⇒ 3 cot β − 3 cot γ = 4 cot ( α + β ) − 2 cot γ
3 cot β − cot γ = 4 ( cot α cot β − 1 ) cot α + cot β 3\cot\beta - \cot\gamma = \frac{4(\cot\alpha\cot\beta - 1)}{\cot\alpha + \cot\beta} 3 cot β − cot γ = c o t α + c o t β 4 ( c o t α c o t β − 1 )
3 cot 2 β − cot β cot γ + 3 cot α cot β − cot α cot γ = 4 cot α cot β − 4 3\cot^2\beta - \cot\beta\cot\gamma + 3\cot\alpha\cot\beta - \cot\alpha\cot\gamma = 4\cot\alpha\cot\beta - 4 3 cot 2 β − cot β cot γ + 3 cot α cot β − cot α cot γ = 4 cot α cot β − 4
4 + 4 cot 2 β = cot 2 β + cot α cot β + cot β cot γ + cot α cot γ 4 + 4\cot^2\beta = \cot^2\beta + \cot\alpha\cot\beta + \cot\beta\cot\gamma + \cot\alpha\cot\gamma 4 + 4 cot 2 β = cot 2 β + cot α cot β + cot β cot γ + cot α cot γ
4 ( 1 + cot 2 β ) = ( cot β + cot α ) ( cot β + cot γ ) 4(1 + \cot^2\beta) = (\cot\beta + \cot\alpha)(\cot\beta + \cot\gamma) 4 ( 1 + cot 2 β ) = ( cot β + cot α ) ( cot β + cot γ )
4 ( 1 + 1 t 2 2 ) = ( 1 t 1 + 1 t 2 ) ( 1 t 2 + 1 t 3 ) 4\left(1 + \frac{1}{t_2^2}\right) = \left(\frac{1}{t_1} + \frac{1}{t_2}\right)\left(\frac{1}{t_2} + \frac{1}{t_3}\right) 4 ( 1 + t 2 2 1 ) = ( t 1 1 + t 2 1 ) ( t 2 1 + t 3 1 )
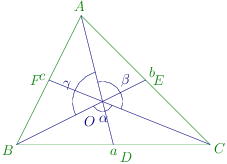
The diagram is given below:
Let the medians be A D , B E AD, BE A D , BE C F CF CF O . O. O .
∠ B O C = α , ∠ C O A = β , ∠ A O B = γ \angle BOC=\alpha, \angle COA = \beta, \angle AOB = \gamma ∠ BOC = α , ∠ CO A = β , ∠ A OB = γ
Let A D = p 1 , B E = p 2 , C F = p 3 AD = p_1, BE=p_2, CF = p_3 A D = p 1 , BE = p 2 , CF = p 3
A O : O D = 2 : 1 ⇒ A O = 2 3 p 1 AO:OD = 2:1 \Rightarrow AO = \frac{2}{3}p_1 A O : O D = 2 : 1 ⇒ A O = 3 2 p 1
Similalrly, O B = 2 3 p 2 , O C = 2 3 p 3 OB = \frac{2}{3}p_2, OC = \frac{2}{3}p_3 OB = 3 2 p 2 , OC = 3 2 p 3
Applying cosine rule in △ A O C , \triangle AOC, △ A OC ,
cos β = O A 2 + O C 2 − A C 2 2. O A . O C = 4 9 p 1 2 + 4 9 p 3 2 − b 2 2. 2 3 p 1 2 3 p 3 \cos\beta = \frac{OA^2 + OC^2 - AC^2}{2.OA.OC} = \frac{\frac{4}{9}p_1^2 + \frac{4}{9}p_3^2 -
b^2}{2.\frac{2}{3}p_1\frac{2}{3}p_3} cos β = 2. O A . OC O A 2 + O C 2 − A C 2 = 2. 3 2 p 1 3 2 p 3 9 4 p 1 2 + 9 4 p 3 2 − b 2
cos β = 4 p 1 2 + 4 p 3 2 − 9 b 2 8 p 1 p 3 \cos\beta = \frac{4p_1^2 + 4p_3^2 - 9b^2}{8p_1p_3} cos β = 8 p 1 p 3 4 p 1 2 + 4 p 3 2 − 9 b 2
Δ A O C = 1 2 . O A . O C . sin β \Delta AOC = \frac{1}{2}.OA.OC.\sin\beta Δ A OC = 2 1 . O A . OC . sin β
1 3 Δ = 1 2 2 3 p 1 2 3 p 3 sin β \frac{1}{3}\Delta = \frac{1}{2}\frac{2}{3}p_1\frac{2}{3}p_3\sin\beta 3 1 Δ = 2 1 3 2 p 1 3 2 p 3 sin β Δ \Delta Δ A B C . ABC. A BC .
sin β = 3 Δ 2 p 1 p 3 \sin\beta = \frac{3\Delta}{2p_1p_3} sin β = 2 p 1 p 3 3Δ
⇒ cos β = 4 p 1 2 + 4 p 3 2 − 9 b 2 12 Δ \Rightarrow \cos\beta = \frac{4p_1^2 + 4p_3^2 - 9b^2}{12\Delta} ⇒ cos β = 12Δ 4 p 1 2 + 4 p 3 2 − 9 b 2
∵ A D \because AD ∵ A D △ A B C \triangle ABC △ A BC
∴ A B 2 + A C 2 = 2 B D 2 + 2 A D 2 \therefore AB^2 + AC^2 = 2BD^2 + 2AD^2 ∴ A B 2 + A C 2 = 2 B D 2 + 2 A D 2
⇒ b 2 + c 2 = 2 a 2 4 + 2 p 1 2 \Rightarrow b^2 + c^2 = 2\frac{a^2}{4} + 2p_1^2 ⇒ b 2 + c 2 = 2 4 a 2 + 2 p 1 2
p 1 2 = 2 b 2 + 2 c 2 − a 2 4 p_1^2 = \frac{2b^2 + 2c^2 - a^2}{4} p 1 2 = 4 2 b 2 + 2 c 2 − a 2
Similarly, p 2 2 = 2 c 2 + 2 a 2 − b 2 4 p_2^2 = \frac{2c^2 + 2a^2 - b^2}{4} p 2 2 = 4 2 c 2 + 2 a 2 − b 2
and p 3 2 = 2 a 2 + 2 b 2 − c 2 4 p_3^2 = \frac{2a^2 + 2b^2 - c^2}{4} p 3 2 = 4 2 a 2 + 2 b 2 − c 2
⇒ cos β = ( 2 b 2 + 2 c 2 − a 2 ) + ( 2 a 2 + 2 b 2 − c 2 ) − 9 b 2 12 Δ \Rightarrow \cos\beta = \frac{(2b^2 + 2c^2 - a^2) + (2a^2 + 2b^2 - c^2) - 9b^2}{12\Delta} ⇒ cos β = 12Δ ( 2 b 2 + 2 c 2 − a 2 ) + ( 2 a 2 + 2 b 2 − c 2 ) − 9 b 2
= a 2 + c 2 − 5 b 2 12 Δ = \frac{a^2 + c^2 - 5b^2}{12\Delta} = 12Δ a 2 + c 2 − 5 b 2
Similarly, cos α = b 2 + c 2 − 5 a 2 12 Δ \cos\alpha = \frac{b^2 + c^2 - 5a^2}{12\Delta} cos α = 12Δ b 2 + c 2 − 5 a 2
Similarly, cos γ = a 2 + b 2 − 5 c 2 12 Δ \cos\gamma = \frac{a^2 + b^2 - 5c^2}{12\Delta} cos γ = 12Δ a 2 + b 2 − 5 c 2
cos α + cos β + cos γ = − 3 ( a 2 + b 2 + c 2 ) 12 Δ \cos\alpha + \cos\beta + \cos\gamma = \frac{-3(a^2 + b^2 + c^2)}{12\Delta} cos α + cos β + cos γ = 12Δ − 3 ( a 2 + b 2 + c 2 )
= − a 2 + b 2 + c 2 4 Δ = -\frac{a^2 + b^2 + c^2}{4\Delta} = − 4Δ a 2 + b 2 + c 2
cot A + cot B + cot C = b 2 + c 2 − a 2 2 b c sin A + c 2 + a 2 − b 2 2 c a sin B + a 2 + b 2 − c 2 2 a b sin C \cot A + \cot B + \cot C = \frac{b^2 + c^2 - a^2}{2bc\sin A} + \frac{c^2 + a^2 - b^2}{2ca\sin B} + \frac{a^2 + b^2 -
c^2}{2ab\sin C} cot A + cot B + cot C = 2 b c s i n A b 2 + c 2 − a 2 + 2 c a s i n B c 2 + a 2 − b 2 + 2 ab s i n C a 2 + b 2 − c 2
= a 2 + b 2 + c 2 4 Δ = \frac{a^2 + b^2 + c^2}{4\Delta} = 4Δ a 2 + b 2 + c 2
⇒ cot α + cot β + cot γ + cot A + cot B + cot C = 0 \Rightarrow \cot\alpha + \cot\beta + \cot\gamma + \cot A + \cot B + \cot C = 0 ⇒ cot α + cot β + cot γ + cot A + cot B + cot C = 0
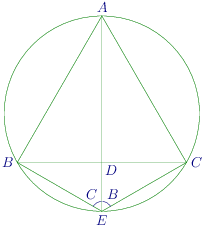
The diagram is given below:
Let A D AD A D A A A B C . BC. BC . A D AD A D E . E. E . D E = α . DE=\alpha. D E = α .
Since angles in the same segment are equal, ∴ ∠ A E B = ∠ A C B = ∠ C \therefore \angle AEB = \angle ACB = \angle C ∴ ∠ A EB = ∠ A CB = ∠ C
and ∠ A E C = ∠ A B C = ∠ B \angle AEC = \angle ABC = \angle B ∠ A EC = ∠ A BC = ∠ B
From right angled △ B D E , tan C = B D D E \triangle BDE, \tan C = \frac{BD}{DE} △ B D E , tan C = D E B D
From right angled △ C D E , tan B = C D D E \triangle CDE, \tan B = \frac{CD}{DE} △ C D E , tan B = D E C D
tan B + tan C = a α \tan B + \tan C = \frac{a}{\alpha} tan B + tan C = α a
Similarly, tan C + tan A = b β \tan C + \tan A = \frac{b}{\beta} tan C + tan A = β b
and tan A + tan B = c γ \tan A + \tan B = \frac{c}{\gamma} tan A + tan B = γ c
Adding, we get
a α + b β + c γ = 2 ( tan A + tan B + tan C ) \frac{a}{\alpha} + \frac{b}{\beta} + \frac{c}{\gamma} = 2(\tan A + \tan B + \tan C) α a + β b + γ c = 2 ( tan A + tan B + tan C )
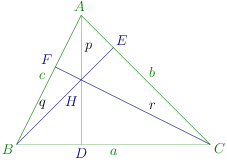
The diagram is given below:
Let H H H A B C . ABC. A BC .
From question, H A = p , H B = q , H C = r . HA = p, HB = q, HC = r. H A = p , H B = q , H C = r .
From figure, ∠ H B D = ∠ E B C = 9 0 ∘ − C \angle HBD = \angle EBC = 90^\circ - C ∠ H B D = ∠ EBC = 9 0 ∘ − C
∠ H C D = ∠ F C B = 9 0 ∘ − B \angle HCD = \angle FCB = 90^\circ - B ∠ H C D = ∠ FCB = 9 0 ∘ − B
∴ ∠ B H C = 18 0 ∘ − ( ∠ H B D + ∠ H C D ) \therefore \angle BHC = 180^\circ - (\angle HBD + \angle HCD) ∴ ∠ B H C = 18 0 ∘ − ( ∠ H B D + ∠ H C D )
= 18 0 ∘ − [ 9 0 ∘ − C + 9 0 ∘ − B ] = B + C = π − A = 180^\circ - [90^\circ - C + 90^\circ - B] = B + C = \pi - A = 18 0 ∘ − [ 9 0 ∘ − C + 9 0 ∘ − B ] = B + C = π − A
Similarly, ∠ A H C = π − B \angle AHC = \pi - B ∠ A H C = π − B ∠ A H B = π − C \angle AHB = \pi - C ∠ A H B = π − C
Now Δ B H C + Δ C H A + Δ A H B = Δ A B C \Delta BHC + \Delta CHA + \Delta AHB = \Delta ABC Δ B H C + Δ C H A + Δ A H B = Δ A BC
⇒ 1 2 [ q r sin B H C + r p sin C H A + p q sin A H B ] = Δ \Rightarrow \frac{1}{2}[qr\sin BHC + rp\sin CHA + pq \sin AHB] = \Delta ⇒ 2 1 [ q r sin B H C + r p sin C H A + pq sin A H B ] = Δ
⇒ 1 2 [ q r sin A + r p sin B + p q sin C ] = Δ \Rightarrow \frac{1}{2}[qr\sin A + rp\sin B + pq\sin C] = \Delta ⇒ 2 1 [ q r sin A + r p sin B + pq sin C ] = Δ
⇒ a q r + b r p + c p q = a b c \Rightarrow aqr + brp + cpq = abc ⇒ a q r + b r p + c pq = ab c
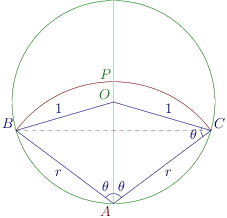
The diagram is given below:
Let O O O A A A B P C BPC BPC
i.e area of the curve A B P C A = 1 2 ABPCA = \frac{1}{2} A BPC A = 2 1 = π 2 = \frac{\pi}{2} = 2 π
Let the radius of this new circle be r . r. r .
Then, A C = A B = A P = r AC = AB = AP = r A C = A B = A P = r
∵ O B = O C = 1 ∴ ∠ O C A = ∠ O A C = θ \because OB = OC = 1 \therefore \angle OCA = \angle OAC = \theta ∵ OB = OC = 1 ∴ ∠ OC A = ∠ O A C = θ
Applying sine rule in △ A O C , \triangle AOC, △ A OC ,
r sin ( π − 2 θ ) = 1 sin θ \frac{r}{\sin(\pi -2\theta)} = \frac{1}{\sin\theta} s i n ( π − 2 θ ) r = s i n θ 1
r = 2 cos θ r = 2\cos\theta r = 2 cos θ
Now area of A B P C A = 2 [ ABPCA = 2[ A BPC A = 2 [ A C P + ACP + A CP + O A C − OAC - O A C − △ O A C ] \triangle OAC] △ O A C ]
= 2 [ 1 2 r 2 θ + 1 2 1 2 ( π − 2 θ ) − 1 2 sin ( π − 2 θ ) ] = 2\left[\frac{1}{2}r^2\theta + \frac{1}{2}1^2(\pi - 2\theta) - \frac{1}{2}\sin(\pi -2\theta)\right] = 2 [ 2 1 r 2 θ + 2 1 1 2 ( π − 2 θ ) − 2 1 sin ( π − 2 θ ) ]
= θ . 4 cos 2 θ + π − 2 θ − sin 2 θ [ ∵ r = 2 cos θ ] =\theta. 4\cos^2\theta + \pi - 2\theta - \sin2\theta [\because r = 2\cos\theta] = θ .4 cos 2 θ + π − 2 θ − sin 2 θ [ ∵ r = 2 cos θ ]
= 2 θ cos 2 θ − sin 2 θ + π = 2\theta\cos2\theta - \sin2\theta + \pi = 2 θ cos 2 θ − sin 2 θ + π
⇒ π 2 = 2 θ cos 2 θ − sin 2 θ + π \Rightarrow \frac{\pi}{2} = 2\theta\cos2\theta - \sin2\theta + \pi ⇒ 2 π = 2 θ cos 2 θ − sin 2 θ + π
⇒ π 2 = sin 2 θ − 2 θ cos 2 θ \Rightarrow \frac{\pi}{2} = \sin2\theta - 2\theta\cos2\theta ⇒ 2 π = sin 2 θ − 2 θ cos 2 θ
The diagram is given below:
Let E F EF EF B C BC BC O O O
Let B F = F C = a ⇒ B C = E F = 2 a BF = FC = a \Rightarrow BC = EF = 2a BF = FC = a ⇒ BC = EF = 2 a O E = O F = a OE=OF = a OE = OF = a
Let O P = x ⇒ O Q = x OP = x \Rightarrow OQ = x OP = x ⇒ OQ = x
⇒ P F = a − x , Q F = a + x \Rightarrow PF = a - x, QF = a + x ⇒ PF = a − x , QF = a + x
From right angled △ B P F , \triangle BPF, △ BPF ,
tan B = P F B F = a − x x \tan B = \frac{PF}{BF} = \frac{a - x}{x} tan B = BF PF = x a − x
From right angled △ Q F C , \triangle QFC, △ QFC ,
tan C = a + x a \tan C = \frac{a + x}{a} tan C = a a + x
⇒ ( tan B − tan C ) 2 = 4 x 2 a 2 \Rightarrow (\tan B - \tan C)^2 = \frac{4x^2}{a^2} ⇒ ( tan B − tan C ) 2 = a 2 4 x 2
In triangle A B C , ABC, A BC ,
tan A = tan [ π − ( B + C ) ] = − tan ( B + C ) = − 2 a 2 x 2 \tan A = \tan[\pi - (B + C)] = -\tan(B + C) = -\frac{2a^2}{x^2} tan A = tan [ π − ( B + C )] = − tan ( B + C ) = − x 2 2 a 2
⇒ tan A ( tan B − tan C ) 2 + 8 = 0 \Rightarrow \tan A(\tan B - \tan C)^2 + 8 = 0 ⇒ tan A ( tan B − tan C ) 2 + 8 = 0
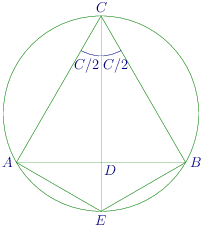
The diagram is given below:
∵ C D \because CD ∵ C D ∠ C \angle C ∠ C
∴ A D D B = b a \therefore \frac{AD}{DB} = \frac{b}{a} ∴ D B A D = a b
⇒ B D = a c a + b \Rightarrow BD = \frac{ac}{a + b} ⇒ B D = a + b a c
Since angles of the same segment are equal.
∴ ∠ A B E = ∠ A C E = C 2 \therefore \angle ABE = \angle ACE = \frac{C}{2} ∴ ∠ A BE = ∠ A CE = 2 C
and ∠ B E C = ∠ B A C = A \angle BEC = \angle BAC = A ∠ BEC = ∠ B A C = A
Applying sine rule in △ B E C , \triangle BEC, △ BEC ,
C E sin C B E = B C sin B E C ⇒ C E = a sin ( a + C 2 ) sin A \frac{CE}{\sin CBE} = \frac{BC}{\sin BEC} \Rightarrow CE = \frac{a\sin\left(a + \frac{C}{2}\right)}{\sin A} s i n CBE CE = s i n BEC BC ⇒ CE = s i n A a s i n ( a + 2 C )
Applying sine rule in △ B D E , \triangle BDE, △ B D E ,
D E sin C 2 = B D sin A ⇒ D E = a c sin C 2 ( a + b ) sin A \frac{DE}{\sin\frac{C}{2}} = \frac{BD}{\sin A}\Rightarrow DE = \frac{ac\sin\frac{C}{2}}{(a + b)\sin A} s i n 2 C D E = s i n A B D ⇒ D E = ( a + b ) s i n A a c s i n 2 C
⇒ C E D E = a sin ( B + C 2 ) a c sin C 2 ( a + b ) \Rightarrow \frac{CE}{DE} = \frac{a\sin\left(B + \frac{C}{2}\right)}{ac\sin\frac{C}{2}}(a + b) ⇒ D E CE = a c s i n 2 C a s i n ( B + 2 C ) ( a + b )
⇒ C E D E = ( a + b ) sin ( B + C 2 ) c sin C 2 \Rightarrow \frac{CE}{DE} = \frac{(a + b)\sin\left(B + \frac{C}{2}\right)}{c\sin \frac{C}{2}} ⇒ D E CE = c s i n 2 C ( a + b ) s i n ( B + 2 C )
Now, sin ( B + C 2 ) sin C 2 = sin ( B + C 2 ) . 2 cos C 2 2 sin C 2 cos C 2 \frac{\sin\left(B + \frac{C}{2}\right)}{\sin\frac{C}{2}} = \frac{\sin\left(B +
\frac{C}{2}\right).2\cos\frac{C}{2}}{2\sin\frac{C}{2}\cos\frac{C}{2}} s i n 2 C s i n ( B + 2 C ) = 2 s i n 2 C c o s 2 C s i n ( B + 2 C ) .2 c o s 2 C
= sin ( B + C ) + sin B sin C = sin A + sin B sin C = a + b c = \frac{\sin(B + C)+ \sin B}{\sin C} = \frac{\sin A + \sin B}{\sin C} = \frac{a + b}{c} = s i n C s i n ( B + C ) + s i n B = s i n C s i n A + s i n B = c a + b
Thus, C E D E = ( a + b ) 2 c 2 \frac{CE}{DE} = \frac{(a + b)^2}{c^2} D E CE = c 2 ( a + b ) 2
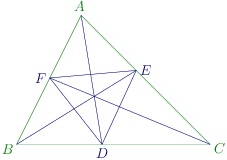
The diagram is given below:
∵ A D \because AD ∵ A D A , A, A ,
B D D C = B A A C = c b \frac{BD}{DC} = \frac{BA}{AC} = \frac{c}{b} D C B D = A C B A = b c
⇒ B D c = D C b = B D + D C b + c \Rightarrow \frac{BD}{c} = \frac{DC}{b} = \frac{BD + DC}{b + c} ⇒ c B D = b D C = b + c B D + D C
⇒ B D c = a b + c \Rightarrow \frac{BD}{c} = \frac{a}{b + c} ⇒ c B D = b + c a
Similarly, B F a = c a + b \frac{BF}{a} = \frac{c}{a + b} a BF = a + b c
Now Δ B D F Δ A B C = B D . B F . sin B a . c . sin B = a c ( a + b ) ( b + c ) \frac{\Delta BDF}{\Delta ABC} = \frac{BD.BF.\sin B}{a.c.\sin B} = \frac{ac}{(a + b)(b + c)} Δ A BC Δ B D F = a . c . s i n B B D . BF . s i n B = ( a + b ) ( b + c ) a c
Similarly, Δ C D E Δ A B C = a b ( a + c ) ( b + c ) \frac{\Delta CDE}{\Delta ABC} = \frac{ab}{(a + c)(b + c)} Δ A BC Δ C D E = ( a + c ) ( b + c ) ab
and Δ A E F Δ A B C = b c ( a + b ) ( a + c ) \frac{\Delta AEF}{\Delta ABC} = \frac{bc}{(a + b)(a + c)} Δ A BC Δ A EF = ( a + b ) ( a + c ) b c
∴ Δ D E F Δ A B C = Δ A B C − ( Δ B D F + Δ C D E + Δ A E F ) Δ A B C \therefore \frac{\Delta DEF}{\Delta ABC} = \frac{\Delta ABC - (\Delta BDF + \Delta CDE + \Delta AEF)}{\Delta ABC} ∴ Δ A BC Δ D EF = Δ A BC Δ A BC − ( Δ B D F + Δ C D E + Δ A EF )
= 1 − a c ( a + b ) ( b + c ) − a b ( a + c ) ( b + c ) − b c ( a + b ) ( a + c ) = 1 - \frac{ac}{(a + b)(b + c)} - \frac{ab}{(a + c)(b + c)} - \frac{bc}{(a + b)(a + c)} = 1 − ( a + b ) ( b + c ) a c − ( a + c ) ( b + c ) ab − ( a + b ) ( a + c ) b c
= 2 a b c ( a + b ) ( b + c ) ( c + a ) = \frac{2abc}{(a + b)(b + c)(c + a)} = ( a + b ) ( b + c ) ( c + a ) 2 ab c
Δ D E F = 2. Δ . a b c ( a + b ) ( b + c ) ( c + a ) \Delta DEF = \frac{2.\Delta .abc}{(a + b)(b + c)(c + a)} Δ D EF = ( a + b ) ( b + c ) ( c + a ) 2.Δ. ab c
The diagram is given below:
∵ A + B + C = π ⇒ 3 α + 3 β + 3 γ = π ⇒ α + β + γ = π 3 \because A + B + C = \pi \Rightarrow 3\alpha + 3\beta + 3\gamma = \pi \Rightarrow \alpha + \beta + \gamma =
\frac{\pi}{3} ∵ A + B + C = π ⇒ 3 α + 3 β + 3 γ = π ⇒ α + β + γ = 3 π
Clearly, ∠ A D B = 6 0 ∘ \angle ADB = 60^\circ ∠ A D B = 6 0 ∘
Applying sine rule in △ A D B , \triangle ADB, △ A D B ,
A R sin β = c sin [ π − ( α + β ) ] \frac{AR}{\sin\beta} = \frac{c}{\sin[\pi - (\alpha + \beta)]} s i n β A R = s i n [ π − ( α + β )] c
A R = c sin β sin ( α + β ) = 2 R sin C sin β sin ( α + β ) AR = \frac{c\sin \beta}{\sin(\alpha + \beta)} = \frac{2R\sin C\sin\beta}{\sin(\alpha + \beta)} A R = s i n ( α + β ) c s i n β = s i n ( α + β ) 2 R s i n C s i n β
= 2 R sin 3 γ sin β sin ( 6 0 ∘ − γ ) = \frac{2R\sin3\gamma\sin\beta}{\sin(60^\circ - \gamma)} = s i n ( 6 0 ∘ − γ ) 2 R s i n 3 γ s i n β
= 2 R ( 3 sin γ − 4 sin 3 γ ) sin β sin ( 6 0 ∘ − γ ) . cos ( 3 0 ∘ − γ ) c o s ( 3 0 ∘ − γ = \frac{2R(3\sin\gamma - 4\sin^3\gamma)\sin\beta}{\sin(60^\circ - \gamma)}.\frac{\cos(30^\circ -
\gamma)}{cos(30^\circ - \gamma} = s i n ( 6 0 ∘ − γ ) 2 R ( 3 s i n γ − 4 s i n 3 γ ) s i n β . cos ( 3 0 ∘ − γ c o s ( 3 0 ∘ − γ )
= 4 R sin β sin γ . ( 3 − 4 sin 2 γ ) . cos ( 3 0 ∘ − γ ) sin ( 0 9 ∘ − 2 γ ) + sin 3 0 ∘ = \frac{4R\sin\beta\sin\gamma.(3 - 4\sin^2\gamma).\cos(30^\circ - \gamma)}{\sin(09^\circ - 2\gamma) + \sin 30^\circ} = s i n ( 0 9 ∘ − 2 γ ) + s i n 3 0 ∘ 4 R s i n β s i n γ . ( 3 − 4 s i n 2 γ ) . c o s ( 3 0 ∘ − γ )
= 4 R sin β sin γ cos ( 3 0 ∘ − γ ) ( 3 − 4 sin 2 γ ) cos 2 γ + 1 2 = \frac{4R\sin\beta\sin\gamma\cos(30^\circ - \gamma)(3 - 4\sin^2\gamma)}{\cos2\gamma + \frac{1}{2}} = c o s 2 γ + 2 1 4 R s i n β s i n γ c o s ( 3 0 ∘ − γ ) ( 3 − 4 s i n 2 γ )
= 8 R sin β sin γ cos ( 3 0 ∘ − γ ) ( 3 − 4 sin 2 γ ) 2 cos 2 γ + 1 = \frac{8R\sin\beta\sin\gamma\cos(30^\circ - \gamma)(3 - 4\sin^2\gamma)}{2\cos2\gamma + 1} = 2 c o s 2 γ + 1 8 R s i n β s i n γ c o s ( 3 0 ∘ − γ ) ( 3 − 4 s i n 2 γ )
= 8 R sin β sin γ cos ( 3 0 ∘ − γ ) ( 3 − 4 sin 2 γ ) 2 ( 1 − 2 sin 2 γ ) + 1 = \frac{8R\sin\beta\sin\gamma\cos(30^\circ - \gamma)(3 - 4\sin^2\gamma)}{2(1 - 2\sin^2\gamma) + 1} = 2 ( 1 − 2 s i n 2 γ ) + 1 8 R s i n β s i n γ c o s ( 3 0 ∘ − γ ) ( 3 − 4 s i n 2 γ )
= 8 R sin β sin γ cos ( 3 0 ∘ − γ ) = 8R\sin\beta\sin\gamma\cos(30^\circ - \gamma) = 8 R sin β sin γ cos ( 3 0 ∘ − γ )
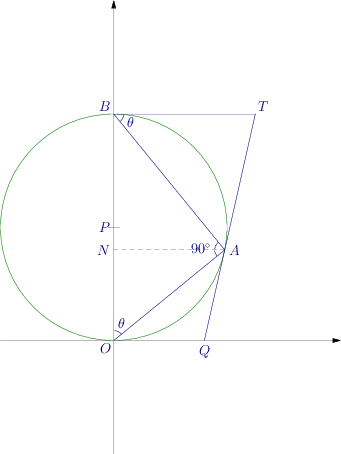
The diagram is given below:
From figure, ∠ A O X = π 2 − θ \angle AOX = \frac{\pi}{2} - \theta ∠ A OX = 2 π − θ
Since O X OX OX O B OB OB P P P O B OB OB
⇒ ∠ O A B = 9 0 ∘ ⇒ ∠ O B A = 9 0 ∘ − θ \Rightarrow \angle OAB = 90^\circ \Rightarrow \angle OBA = 90^\circ - \theta ⇒ ∠ O A B = 9 0 ∘ ⇒ ∠ OB A = 9 0 ∘ − θ
By property of circle, O A Q = ∠ O B A = 9 0 ∘ − θ OAQ = \angle OBA = 90^\circ - \theta O A Q = ∠ OB A = 9 0 ∘ − θ
Also, A O Q = 9 0 ∘ − t h e t a [ ∵ O Q = O A ] AOQ = 90^\circ - theta[\because OQ = OA] A OQ = 9 0 ∘ − t h e t a [ ∵ OQ = O A ]
∴ O Q A = 2 θ ⇒ A Q X = π − 2 θ \therefore OQA = 2\theta \Rightarrow AQX = \pi - 2\theta ∴ OQ A = 2 θ ⇒ A QX = π − 2 θ
∠ B O X = π 1 \angle BOX = \frac{\pi}{1} ∠ BOX = 1 π
Applying sine rule in △ A B T , w e g e t \triangle ABT, we get △ A BT , w e g e t
A B sin ( π − 2 θ ) = A T sin θ \frac{AB}{\sin(\pi - 2\theta)} = \frac{AT}{\sin\theta} s i n ( π − 2 θ ) A B = s i n θ A T
A B sin 2 θ = t sin θ ⇒ A B = 2 t cos θ \frac{AB}{\sin2\theta} = \frac{t}{\sin\theta} \Rightarrow AB = 2t\cos\theta s i n 2 θ A B = s i n θ t ⇒ A B = 2 t cos θ
From right angled △ A O B , \triangle AOB, △ A OB ,
tan θ = A B O A ⇒ A B = c tan θ \tan\theta = \frac{AB}{OA} \Rightarrow AB = c\tan\theta tan θ = O A A B ⇒ A B = c tan θ
⇒ c tan θ = 2 t cos θ \Rightarrow c\tan\theta = 2t\cos\theta ⇒ c tan θ = 2 t cos θ
⇒ c sin θ − t ( 1 + cos 2 θ ) = 0 \Rightarrow c\sin\theta - t(1 + \cos2\theta) = 0 ⇒ c sin θ − t ( 1 + cos 2 θ ) = 0
Let A N ⊥ O B AN\perp OB A N ⊥ OB
Now, O N + N B = O B ON + NB = OB ON + NB = OB
⇒ c cos θ + A B sin θ = d \Rightarrow c\cos\theta + AB\sin\theta = d ⇒ c cos θ + A B sin θ = d
⇒ c cos θ + 2 t sin θ cos θ = d \Rightarrow c\cos\theta + 2t\sin\theta\cos\theta = d ⇒ c cos θ + 2 t sin θ cos θ = d
⇒ c cos θ + t sin 2 θ = d \Rightarrow c\cos\theta + t\sin2\theta = d ⇒ c cos θ + t sin 2 θ = d
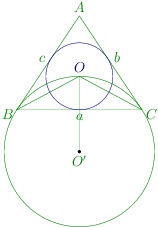
Since A D AD A D ∴ B D = D C = a 2 \therefore BD = DC = \frac{a}{2} ∴ B D = D C = 2 a
Also, ∵ ∠ D A E = ∠ C A E = A 3 \because \angle DAE = \angle CAE = \frac{A}{3} ∵ ∠ D A E = ∠ C A E = 3 A
A E AE A E ∠ A E D = a n g l e A E C = 9 0 ∘ \angle AED = angle AEC = 90^\circ ∠ A E D = an g l e A EC = 9 0 ∘
∴ A D = A C = b \therefore AD = AC = b ∴ A D = A C = b
Applying cosine rule in △ A B D , \triangle ABD, △ A B D ,
cos A 3 = A B 2 + A D 2 − B D 2 2. A B . A D \cos\frac{A}{3} = \frac{AB^2 + AD^2 - BD^2}{2.AB.AD} cos 3 A = 2. A B . A D A B 2 + A D 2 − B D 2
= c 2 + b 2 − a 2 4 2. c . b = 4 b 2 + 4 c 2 − a 2 8 b c = \frac{c^2 + b^2 - \frac{a^2}{4}}{2.c.b} = \frac{4b^2 + 4c^2 - a^2}{8bc} = 2. c . b c 2 + b 2 − 4 a 2 = 8 b c 4 b 2 + 4 c 2 − a 2
Applying cosine rule in △ A B C , \triangle ABC, △ A BC ,
cos A = b 2 + c 2 − a 2 2 b c \cos A = \frac{b^2 + c^2 - a^2}{2bc} cos A = 2 b c b 2 + c 2 − a 2
4 cos 3 A 3 − 3 cos A 3 = b 2 + c 2 − a 2 2 b c 4\cos^3\frac{A}{3} - 3\cos\frac{A}{3} = \frac{b^2 + c^2 - a^2}{2bc} 4 cos 3 3 A − 3 cos 3 A = 2 b c b 2 + c 2 − a 2
⇒ 4 cos 3 A 3 − 4 cos A 3 = b 2 + c 2 − a 2 2 b c − 4 b 2 + 4 c 2 − a 2 8 b c \Rightarrow 4\cos^3\frac{A}{3} - 4\cos\frac{A}{3} = \frac{b^2 + c^2 - a^2}{2bc} - \frac{4b^2 + 4c^2 - a^2}{8bc} ⇒ 4 cos 3 3 A − 4 cos 3 A = 2 b c b 2 + c 2 − a 2 − 8 b c 4 b 2 + 4 c 2 − a 2
⇒ 4 cos A 3 ( 1 − cos 2 A 3 ) = 4 b 2 + 4 c 2 − a 2 8 b c − b 2 + c 2 − a 2 2 b c \Rightarrow 4\cos\frac{A}{3}\left(1 - \cos^2\frac{A}{3}\right) = \frac{4b^2 + 4c^2 - a^2}{8bc} - \frac{b^2 + c^2 -
a^2}{2bc} ⇒ 4 cos 3 A ( 1 − cos 2 3 A ) = 8 b c 4 b 2 + 4 c 2 − a 2 − 2 b c b 2 + c 2 − a 2
⇒ cos A 3 . sin 2 A 3 = 3 a 2 32 b c \Rightarrow \cos\frac{A}{3}.\sin^2\frac{A}{3} = \frac{3a^2}{32bc} ⇒ cos 3 A . sin 2 3 A = 32 b c 3 a 2
Given, cos A + cos B + cos C = 3 2 \cos A + \cos B + \cos C = \frac{3}{2} cos A + cos B + cos C = 2 3
⇒ b 2 + c 2 − a 2 2 b c + c 2 + a 2 − b 2 2 c a + a 2 + b 2 − c 2 2 a b = 3 2 \Rightarrow \frac{b^2 + c^2 - a^2}{2bc} + \frac{c^2 + a^2 - b^2}{2ca} + \frac{a^2 + b^2 - c^2}{2ab} = \frac{3}{2} ⇒ 2 b c b 2 + c 2 − a 2 + 2 c a c 2 + a 2 − b 2 + 2 ab a 2 + b 2 − c 2 = 2 3
⇒ a ( b 2 + c 2 − a 2 ) + b ( c 2 + a 2 − b 2 ) + c ( a 2 + b 2 − c 2 ) = 3 a b c \Rightarrow a(b^2 + c^2 - a^2) + b(c^2 + a^2 - b^2) + c(a^2 + b^2 - c^2) = 3abc ⇒ a ( b 2 + c 2 − a 2 ) + b ( c 2 + a 2 − b 2 ) + c ( a 2 + b 2 − c 2 ) = 3 ab c
⇒ a ( b − c ) 2 + b ( c − a ) 2 + c ( a − b ) 2 = a 3 + b 3 + c 3 − 3 a b c = 1 2 [ ( a − b ) 2 + ( b − c ) 2 + ( c − a ) 2 ] ( a + b + c ) \Rightarrow a(b - c)^2 + b(c - a)^2 + c(a - b)^2 = a^3 + b^3 + c^3 - 3abc = \frac{1}{2}[(a - b)^2 + (b - c)^2 + (c -
a)^2](a + b + c) ⇒ a ( b − c ) 2 + b ( c − a ) 2 + c ( a − b ) 2 = a 3 + b 3 + c 3 − 3 ab c = 2 1 [( a − b ) 2 + ( b − c ) 2 + ( c − a ) 2 ] ( a + b + c )
⇒ b + c − a 2 ( b − c ) 2 + c + a − b 2 ( c − a ) 2 + a + b − c 2 ( a − b ) 2 = 0 \Rightarrow \frac{b + c - a}{2}(b - c)^2 + \frac{c + a - b}{2}(c - a)^2 + \frac{a + b - c}{2}(a - b)^2 = 0 ⇒ 2 b + c − a ( b − c ) 2 + 2 c + a − b ( c − a ) 2 + 2 a + b − c ( a − b ) 2 = 0
⇒ ( a − b ) 2 = ( b − c ) 2 = ( c − a ) 2 = 0 \Rightarrow (a - b)^2 = (b - c)^2 = (c - a)^2 = 0 ⇒ ( a − b ) 2 = ( b − c ) 2 = ( c − a ) 2 = 0
⇒ a = b = c \Rightarrow a = b = c ⇒ a = b = c
If the △ A B C \triangle ABC △ A BC ⇒ A = B = C = 6 0 ∘ \Rightarrow A = B = C = 60^\circ ⇒ A = B = C = 6 0 ∘
⇒ tan A + tan B + tan C = 3 3 \Rightarrow \tan A + \tan B + \tan C = 3\sqrt{3} ⇒ tan A + tan B + tan C = 3 3
If tan A + tan B + tan C = 3 3 \tan A + \tan B + \tan C = 3\sqrt{3} tan A + tan B + tan C = 3 3
then tan A tan B tan C = 3 3 \tan A\tan B\tan C = 3\sqrt{3} tan A tan B tan C = 3 3
Thus, A.M. of tan A , tan B , tan C = \tan A, \tan B, \tan C = tan A , tan B , tan C = tan A , tan B , tan C \tan A, \tan B, \tan C tan A , tan B , tan C
⇒ tan A = tan B = tan C \Rightarrow \tan A = \tan B = \tan C ⇒ tan A = tan B = tan C
L.H.S. = ( a + b + c ) tan C 2 = 2 R ( sin A + sin B + sin C ) sin C 2 cos C 2 = (a + b + c)\tan\frac{C}{2} = 2R(\sin A + \sin B + \sin C)\frac{\sin\frac{C}{2}}{\cos\frac{C}{2}} = ( a + b + c ) tan 2 C = 2 R ( sin A + sin B + sin C ) c o s 2 C s i n 2 C
= 2 R ( 2 sin A + B 2 cos A − B 2 + 2 sin C 2 cos C 2 ) sin C 2 cos C 2 = 2R\left(2\sin\frac{A + B}{2}\cos\frac{A - B}{2} + 2\sin\frac{C}{2}\cos\frac{C}{2}\right)\frac{\sin\frac{C}{2}}{\cos\frac{C}{2}} = 2 R ( 2 sin 2 A + B cos 2 A − B + 2 sin 2 C cos 2 C ) c o s 2 C s i n 2 C
= 2 R ( 2 cos C 2 cos A − B 2 + 2 sin C 2 cos C 2 ) sin C 2 cos C 2 = 2R\left(2\cos\frac{C}{2}\cos\frac{A - B}{2} +
2\sin\frac{C}{2}\cos\frac{C}{2}\right)\frac{\sin\frac{C}{2}}{\cos\frac{C}{2}} = 2 R ( 2 cos 2 C cos 2 A − B + 2 sin 2 C cos 2 C ) c o s 2 C s i n 2 C
= 2 R ( 2 sin C 2 cos A − B 2 + 2 sin 2 C 2 ) = 2R\left(2\sin\frac{C}{2}\cos\frac{A - B}{2} + 2\sin^2\frac{C}{2}\right) = 2 R ( 2 sin 2 C cos 2 A − B + 2 sin 2 2 C )
= 2 R ( 2 cos A + B 2 cos A − B 2 + 2 sin 2 C 2 ) = 2R\left(2\cos\frac{A + B}{2}\cos\frac{A - B}{2} + 2\sin^2\frac{C}{2}\right) = 2 R ( 2 cos 2 A + B cos 2 A − B + 2 sin 2 2 C )
= 2 R ( cos A + cos B + 2 sin 2 C 2 ) = 2R\left(\cos A + \cos B + 2\sin^2\frac{C}{2}\right) = 2 R ( cos A + cos B + 2 sin 2 2 C )
R.H.S = a cot A 2 + b cot B 2 − c cot C 2 = a\cot\frac{A}{2} + b\cot\frac{B}{2} - c\cot\frac{C}{2} = a cot 2 A + b cot 2 B − c cot 2 C
= 2 R ( sin A cot A 2 = sin B cot B 2 − sin C cot C 2 ) = 2R\left(\sin A\cot\frac{A}{2} = \sin B\cot\frac{B}{2} - \sin C\cot\frac{C}{2}\right) = 2 R ( sin A cot 2 A = sin B cot 2 B − sin C cot 2 C )
= 2 R ( 2 cos 2 A 2 + 2 cos 2 B 2 − 2 cos 2 C 2 ) = 2R\left(2\cos^2\frac{A}{2} + 2\cos^2\frac{B}{2} - 2\cos^2\frac{C}{2}\right) = 2 R ( 2 cos 2 2 A + 2 cos 2 2 B − 2 cos 2 2 C )
= 2 R ( 2 cos 2 A 2 + 2 cos 2 B 2 − 2 + 2 sin 2 C 2 ) = 2R\left(2\cos^2\frac{A}{2} + 2\cos^2\frac{B}{2} - 2 + 2\sin^2\frac{C}{2}\right) = 2 R ( 2 cos 2 2 A + 2 cos 2 2 B − 2 + 2 sin 2 2 C )
= 2 R ( cos A + cos B + 2 sin 2 C 2 ) = 2R\left(\cos A + \cos B + 2\sin^2\frac{C}{2}\right) = 2 R ( cos A + cos B + 2 sin 2 2 C )
Thus, L.H.S. = R.H.S.
sin 2 θ = 1 − cos 2 θ 2 ⇒ sin 4 θ = ( 1 − cos 2 θ ) 2 4 \sin^2\theta = \frac{1 - \cos2\theta}{2} \Rightarrow \sin^4\theta = \frac{(1 - \cos2\theta)^2}{4} sin 2 θ = 2 1 − c o s 2 θ ⇒ sin 4 θ = 4 ( 1 − c o s 2 θ ) 2
Also, for a triangle cos 2 A + cos 2 B + cos 2 C = − 1 − 4 cos A cos B cos C \cos 2A + \cos 2B + \cos 2C = -1 -4\cos A\cos B\cos C cos 2 A + cos 2 B + cos 2 C = − 1 − 4 cos A cos B cos C
and cos 2 2 A + cos 2 B + cos 2 C = 1 + 2 cos 2 A cos 2 B cos 2 C \cos^22A + \cos^2B + \cos^2C = 1 + 2\cos 2A\cos 2B\cos 2C cos 2 2 A + cos 2 B + cos 2 C = 1 + 2 cos 2 A cos 2 B cos 2 C
L.H.S. = ( 1 − cos 2 A ) 2 4 + ( 1 − cos 2 B ) 2 4 + ( 1 − cos 2 C ) 2 4 = \frac{(1 - \cos2A)^2}{4} + \frac{(1 - \cos2B)^2}{4} + \frac{(1 - \cos 2C)^2}{4} = 4 ( 1 − c o s 2 A ) 2 + 4 ( 1 − c o s 2 B ) 2 + 4 ( 1 − c o s 2 C ) 2
= 1 4 [ 3 − 2 ( cos 2 A + cos 2 B + cos 2 C ) + cos 2 2 A + cos 2 2 B + cos 2 2 C ] = \frac{1}{4}[3 - 2(\cos2A +\cos 2B + \cos 2C) + \cos^22A + \cos^22B + \cos^22C] = 4 1 [ 3 − 2 ( cos 2 A + cos 2 B + cos 2 C ) + cos 2 2 A + cos 2 2 B + cos 2 2 C ]
= 1 4 [ 3 − 2 ( − 1 − 4 cos A cos B cos C ) + 1 + 2 cos 2 A cos 2 B cos 2 C ] = \frac{1}{4}[3 - 2(-1 - 4\cos A\cos B\cos C) + 1 + 2\cos 2A\cos 2B\cos 2C] = 4 1 [ 3 − 2 ( − 1 − 4 cos A cos B cos C ) + 1 + 2 cos 2 A cos 2 B cos 2 C ]
= 3 2 + 2 cos A cos B cos C + 1 2 cos 2 A cos 2 B cos 2 C = = \frac{3}{2} + 2\cos A\cos B\cos C + \frac{1}{2}\cos 2A\cos 2B\cos 2C = = 2 3 + 2 cos A cos B cos C + 2 1 cos 2 A cos 2 B cos 2 C =
Observe the relations in previous problem.
L.H.S. = ( 1 + cos 2 A ) 2 4 + ( 1 + cos 2 B ) 2 4 + ( 1 + cos 2 C ) 2 4 = \frac{(1 + \cos2A)^2}{4} + \frac{(1 + \cos2B)^2}{4} + \frac{(1 + \cos2C)^2}{4} = 4 ( 1 + c o s 2 A ) 2 + 4 ( 1 + c o s 2 B ) 2 + 4 ( 1 + c o s 2 C ) 2
= 1 4 [ 3 + 2 ( cos 2 A + cos 2 B + cos 2 C ) + cos 2 2 A + cos 2 2 B + cos 2 2 C ] = \frac{1}{4}[3 + 2(\cos2A +\cos 2B + \cos 2C) + \cos^22A + \cos^22B + \cos^22C] = 4 1 [ 3 + 2 ( cos 2 A + cos 2 B + cos 2 C ) + cos 2 2 A + cos 2 2 B + cos 2 2 C ]
= 1 4 [ 3 + 2 ( − 1 − 4 cos A cos B cos C ) + 1 + 2 cos 2 A cos 2 B cos 2 C ] = \frac{1}{4}[3 + 2(-1 - 4\cos A\cos B\cos C) + 1 + 2\cos 2A\cos 2B\cos 2C] = 4 1 [ 3 + 2 ( − 1 − 4 cos A cos B cos C ) + 1 + 2 cos 2 A cos 2 B cos 2 C ]
= 1 2 − 2 cos A cos B cos C + 1 2 cos 2 A cos 2 B cos 2 C = = \frac{1}{2} - 2\cos A\cos B\cos C + \frac{1}{2}\cos2A\cos2B\cos2C = = 2 1 − 2 cos A cos B cos C + 2 1 cos 2 A cos 2 B cos 2 C =
L.H.S. = cot B + cos C cos A sin B = cos B cos A + cos [ π − ( A + B ) ] cos A sin B = \cot B + \frac{\cos C}{\cos A\sin B} = \frac{\cos B\cos A + \cos[\pi - (A + B)]}{\cos A\sin B} = cot B + c o s A s i n B c o s C = c o s A s i n B c o s B c o s A + c o s [ π − ( A + B )]
= cos B cos A − cos ( A + B ) cos A sin B = sin A sin B cos A sin B = \frac{\cos B\cos A - \cos(A + B)}{\cos A\sin B} = \frac{\sin A\sin B}{\cos A\sin B} = c o s A s i n B c o s B c o s A − c o s ( A + B ) = c o s A s i n B s i n A s i n B
= tan A = \tan A = tan A
R.H.S. = cot C + cos B cos A sin C = cos C cos A + cos [ π − ( A + C ) ] cos A sin C = \cot C + \frac{\cos B}{\cos A\sin C} = \frac{\cos C\cos A + \cos[\pi - (A + C)]}{\cos A\sin C} = cot C + c o s A s i n C c o s B = c o s A s i n C c o s C c o s A + c o s [ π − ( A + C )]
= sin A sin C cos A sin C = tan A = \frac{\sin A\sin C}{\cos A\sin C} = \tan A = c o s A s i n C s i n A s i n C = tan A
Thus, L.H.S. = R.H.S.
a sin ( B − C ) b 2 − c 2 = 1 2 R . sin A sin ( B − C ) sin 2 B − sin 2 C \frac{a\sin(B - C)}{b^2 - c^2} = \frac{1}{2R}.\frac{\sin A\sin(B - C)}{\sin^2B - \sin^2C} b 2 − c 2 a s i n ( B − C ) = 2 R 1 . s i n 2 B − s i n 2 C s i n A s i n ( B − C )
= 1 2 R . sin [ π − ( B + C ) ] sin ( B − C ) sin ( B + C ) sin ( B − C ) = \frac{1}{2R}.\frac{\sin[\pi - (B + C)]\sin(B - C)}{\sin(B + C)\sin(B - C)} = 2 R 1 . s i n ( B + C ) s i n ( B − C ) s i n [ π − ( B + C )] s i n ( B − C )
= 1 2 R [ ∵ sin { π − ( B + C ) = sin ( B + C ) } ] = \frac{1}{2R}[\because \sin\{\pi - (B + C) = \sin(B + C)\}] = 2 R 1 [ ∵ sin { π − ( B + C ) = sin ( B + C )}]
Similarly, b sin ( C − A ) c 2 − a 2 = c sin ( A − B ) a 2 − b 2 = 1 2 R \frac{b\sin(C - A)}{c^2 - a^2} = \frac{c\sin(A - B)}{a^2 - b^2} = \frac{1}{2R} c 2 − a 2 b s i n ( C − A ) = a 2 − b 2 c s i n ( A − B ) = 2 R 1
R.H.S. = b − c a cos A 2 = sin B − sin C sin A cos A 2 = \frac{b - c}{a}\cos\frac{A}{2} = \frac{\sin B - \sin C}{\sin A}\cos\frac{A}{2} = a b − c cos 2 A = s i n A s i n B − s i n C cos 2 A
= 2 cos B + C 2 sin B − C 2 2 sin A 2 cos A 2 cos A 2 = \frac{2\cos\frac{B + C}{2}\sin\frac{B - C}{2}}{2\sin\frac{A}{2}\cos\frac{A}{2}}\cos\frac{A}{2} = 2 s i n 2 A c o s 2 A 2 c o s 2 B + C s i n 2 B − C cos 2 A
= sin A 2 sin B − C 2 sin A 2 = \frac{\sin\frac{A}{2}\sin\frac{B - C}{2}}{\sin\frac{A}{2}} = s i n 2 A s i n 2 A s i n 2 B − C
= sin B − C 2 = = \sin\frac{B - C}{2} = = sin 2 B − C =
L.H.S. = sin 3 A cos ( B − C ) + sin 3 B cos ( C − A ) + sin 3 C cos ( A − B ) = 3 sin A sin B sin C = \sin^3A\cos(B - C) + \sin^3B\cos(C - A) + \sin^3C\cos(A - B) = 3\sin A\sin B\sin C = sin 3 A cos ( B − C ) + sin 3 B cos ( C − A ) + sin 3 C cos ( A − B ) = 3 sin A sin B sin C
= sin 2 A sin ( B + C ) cos ( B − C ) + sin 2 B sin ( C + A ) cos ( C − A ) + sin 2 C sin ( A + B ) cos ( A − B ) = \sin^2A\sin(B + C)\cos(B - C) + \sin^2B\sin(C + A)\cos(C - A) + \sin^2C\sin(A + B)\cos(A - B) = sin 2 A sin ( B + C ) cos ( B − C ) + sin 2 B sin ( C + A ) cos ( C − A ) + sin 2 C sin ( A + B ) cos ( A − B )
= 1 2 [ sin 2 A ( sin 2 B + sin 2 C ) + sin 2 B ( sin 2 C + sin 2 A ) + sin 2 C ( sin 2 A + sin 2 B ) ] = \frac{1}{2}[\sin^2A(\sin 2B + \sin 2C) + \sin^2B(\sin 2C + \sin 2A) + \sin^2C(\sin2A + \sin 2B)] = 2 1 [ sin 2 A ( sin 2 B + sin 2 C ) + sin 2 B ( sin 2 C + sin 2 A ) + sin 2 C ( sin 2 A + sin 2 B )]
= sin 2 A ( sin B cos B + sin C cos C ) + sin 2 B ( sin C cos C + sin A cos A ) + sin 2 C ( sin A cos A + sin B cos B ) = \sin^2A(\sin B\cos B + \sin C\cos C) + \sin^2B(\sin C\cos C + \sin A\cos A) + \sin^2C(\sin A\cos A + \sin B\cos B) = sin 2 A ( sin B cos B + sin C cos C ) + sin 2 B ( sin C cos C + sin A cos A ) + sin 2 C ( sin A cos A + sin B cos B )
= sin A sin B ( sin A cos B + cos A sin B ) + sin B sin C ( sin B cos C + cos B sin C ) + sin A sin C ( sin A cos C + cos A sin C ) = \sin A\sin B(\sin A\cos B + \cos A\sin B) + \sin B\sin C(\sin B\cos C + \cos B\sin C) + \sin A\sin C(\sin A\cos C +
\cos A\sin C) = sin A sin B ( sin A cos B + cos A sin B ) + sin B sin C ( sin B cos C + cos B sin C ) + sin A sin C ( sin A cos C + cos A sin C )
= sin A sin B sin ( A + B ) + sin B sin C sin ( B + C ) + sin A sin C sin ( A + C ) = \sin A\sin B\sin(A + B) + \sin B\sin C\sin(B + C) + \sin A\sin C\sin(A + C) = sin A sin B sin ( A + B ) + sin B sin C sin ( B + C ) + sin A sin C sin ( A + C )
= 3 sin A sin B sin C = = 3\sin A\sin B\sin C = = 3 sin A sin B sin C =
L.H.S. = sin 3 A + sin 3 B + sin 3 C = 3 4 [ sin A + sin B + sin C ] − 1 3 [ sin 3 A + sin 3 B + sin 3 C ] = \sin^3A + \sin^3B + \sin^3C = \frac{3}{4}[\sin A + \sin B + \sin C] - \frac{1}{3}[\sin 3A + \sin 3B + \sin
3C] = sin 3 A + sin 3 B + sin 3 C = 4 3 [ sin A + sin B + sin C ] − 3 1 [ sin 3 A + sin 3 B + sin 3 C ]
sin A + sin B + sin C = 2 sin A + B 2 cos A − B 2 + 2 sin C 2 cos C 2 \sin A + \sin B + \sin C = 2\sin\frac{A + B}{2}\cos\frac{A - B}{2} + 2\sin \frac{C}{2}\cos \frac{C}{2} sin A + sin B + sin C = 2 sin 2 A + B cos 2 A − B + 2 sin 2 C cos 2 C
= 2 cos C 2 [ cos A − B 2 + cos A − B 2 ] = 2\cos\frac{C}{2}\left[\cos\frac{A - B}{2} + \cos\frac{A - B}{2}\right] = 2 cos 2 C [ cos 2 A − B + cos 2 A − B ]
= 4 cos A 2 cos B 2 cos C 2 = 4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2} = 4 cos 2 A cos 2 B cos 2 C
Similarly, sin 3 A + sin 3 B + sin 3 C = 4 cos 3 A 2 cos 3 B 2 cos 3 C 2 \sin3A + \sin3B + \sin3C = 4\cos\frac{3A}{2}\cos\frac{3B}{2}\cos\frac{3C}{2} sin 3 A + sin 3 B + sin 3 C = 4 cos 2 3 A cos 2 3 B cos 2 3 C
sin 3 A sin 3 ( B − C ) = sin 3 A 3 sin ( B − C ) − sin 3 ( B − C ) 4 \sin3A\sin^3(B - C) = \sin3A\frac{3\sin(B - C) - \sin3(B - C)}{4} sin 3 A sin 3 ( B − C ) = sin 3 A 4 3 s i n ( B − C ) − s i n 3 ( B − C )
Now sin 3 A sin 3 ( B − C ) = sin 3 ( B + C ) sin 3 ( B − C ) = sin 2 3 B − sin 2 3 C \sin 3A\sin3(B - C) = \sin3(B + C)\sin3(B - C) = \sin^23B - \sin^23C sin 3 A sin 3 ( B − C ) = sin 3 ( B + C ) sin 3 ( B − C ) = sin 2 3 B − sin 2 3 C
and sin 3 A sin ( B − C ) = ( 3 sin A − 4 sin 3 A ) sin ( B − C ) \sin 3A\sin(B - C) = (3\sin A - 4\sin^3A)\sin(B - C) sin 3 A sin ( B − C ) = ( 3 sin A − 4 sin 3 A ) sin ( B − C )
= 3 sin ( B + C ) sin ( B − C ) − 4 sin 2 A sin ( B + C ) sin ( B − C ) = 3\sin(B + C)\sin(B - C) - 4\sin^2A\sin(B + C)\sin(B - C) = 3 sin ( B + C ) sin ( B − C ) − 4 sin 2 A sin ( B + C ) sin ( B − C )
= 3 [ sin 2 B − sin 2 C ] − 4 sin 2 A ( sin 2 B − sin 2 C ) = 3[\sin^2B - \sin^2C] - 4\sin^2A(\sin^2B - \sin^2C) = 3 [ sin 2 B − sin 2 C ] − 4 sin 2 A ( sin 2 B − sin 2 C )
Thus, sin 3 A sin 3 ( B − C ) + sin 3 B sin 3 ( C − A ) + sin 3 C sin 3 ( A − B ) = 0 \sin3A\sin^3(B - C) + \sin3B\sin^3(C - A) + \sin3C\sin^3(A - B) = 0 sin 3 A sin 3 ( B − C ) + sin 3 B sin 3 ( C − A ) + sin 3 C sin 3 ( A − B ) = 0
sin 3 A cos 3 ( B − C ) = sin 3 A . 3 cos ( B − C ) + cos 3 ( B − C 4 \sin3A\cos^3(B - C) = \sin3A.\frac{3\cos(B - C) + \cos3(B - C}{4} sin 3 A cos 3 ( B − C ) = sin 3 A . 4 3 c o s ( B − C ) + c o s 3 ( B − C
Now, 1 4 sin 3 A cos 3 ( B − C ) = 1 8 2 sin 3 ( B + C ) cos 3 ( B − C ) = 1 8 ( sin 6 B + sin 6 C ) \frac{1}{4}\sin3A \cos3(B - C) = \frac{1}{8}2\sin3(B + C)\cos3(B - C) = \frac{1}{8}(\sin 6B + \sin 6C) 4 1 sin 3 A cos 3 ( B − C ) = 8 1 2 sin 3 ( B + C ) cos 3 ( B − C ) = 8 1 ( sin 6 B + sin 6 C )
So ∑ sin 3 A cos 3 ( B − C ) = 1 4 ( sin 6 A + sin 6 B + sin 6 C ) \sum \sin3A \cos3(B - C) = \frac{1}{4}(\sin 6A + \sin 6B + \sin 6C) ∑ sin 3 A cos 3 ( B − C ) = 4 1 ( sin 6 A + sin 6 B + sin 6 C )
Again, 3 4 sin 3 A . cos ( B − C ) = 3 4 ( 3 sin A − 4 sin 3 A ) cos ( B − C ) \frac{3}{4}\sin3A.\cos(B - C) = \frac{3}{4}(3\sin A - 4\sin^3A)\cos(B - C) 4 3 sin 3 A . cos ( B − C ) = 4 3 ( 3 sin A − 4 sin 3 A ) cos ( B − C )
= 9 8 [ ( sin 2 B + sin 2 C ) − 3 sin 3 A cos ( B − C ) = \frac{9}{8}[(\sin 2B + \sin 2C) -3\sin^3A\cos(B - C) = 8 9 [( sin 2 B + sin 2 C ) − 3 sin 3 A cos ( B − C )
We have just proved that ∑ sin 3 A cos ( B − C ) = 3 sin A sin B sin C \sum \sin^3A\cos(B - C) = 3\sin A\sin B\sin C ∑ sin 3 A cos ( B − C ) = 3 sin A sin B sin C
∴ 9 8 ∑ ( sin 2 B + sin 2 C ) = 9 4 ( sin 2 A + sin 2 B + sin 2 C ) \therefore \frac{9}{8}\sum(\sin2B + \sin 2C) = \frac{9}{4}(\sin 2A + \sin 2B + \sin 2C) ∴ 8 9 ∑ ( sin 2 B + sin 2 C ) = 4 9 ( sin 2 A + sin 2 B + sin 2 C )
and 3 ∑ sin 3 A cos ( B − C ) = 9 sin A sin B sin C 3\sum\sin^3A\cos(B - C) = 9\sin A\sin B\sin C 3 ∑ sin 3 A cos ( B − C ) = 9 sin A sin B sin C
Now, sin 2 A + sin 2 B + sin 2 C = 4 sin A sin B sin C \sin2A + \sin2B + \sin2C = 4\sin A\sin B\sin C sin 2 A + sin 2 B + sin 2 C = 4 sin A sin B sin C
and sin 6 A + sin 6 B + sin 6 C = 4 sin 3 A sin 3 B sin 3 C \sin6A + \sin 6B + \sin6C = 4\sin3A\sin3B\sin3C sin 6 A + sin 6 B + sin 6 C = 4 sin 3 A sin 3 B sin 3 C
Thus, the sum would be sin 3 A sin 3 B sin 3 C \sin 3A\sin3B\sin3C sin 3 A sin 3 B sin 3 C
L.H.S. = ( s ( s − a ) + s ( s − b ) Δ ) ( a . ( s − a ) ( s − c ) a c + b ( s − b ) ( s − c ) b c ) = \left(\frac{s(s - a) + s(s - b)}{\Delta}\right)\left(\frac{a.(s - a)(s - c)}{ac} + \frac{b(s - b)(s -
c)}{bc}\right) = ( Δ s ( s − a ) + s ( s − b ) ) ( a c a . ( s − a ) ( s − c ) + b c b ( s − b ) ( s − c ) )
= s ( 2 s − a − b ) Δ ( ( s − c ) ( 2 s − a − b ) c ) = \frac{s(2s - a - b)}{\Delta}\left(\frac{(s - c)(2s - a - b)}{c}\right) = Δ s ( 2 s − a − b ) ( c ( s − c ) ( 2 s − a − b ) )
= c cot C 2 = = c\cot\frac{C}{2} = = c cot 2 C =
Given a , b , c a,b,c a , b , c ∴ 2 b = a + c \therefore 2b = a + c ∴ 2 b = a + c
2 sin B = sin A + sin C ⇒ 4 sin B 2 cos B 2 = 2 sin A + C 2 cos A − C 2 2\sin B = \sin A + \sin C \Rightarrow 4\sin\frac{B}{2}\cos\frac{B}{2} = 2\sin\frac{A + C}{2}\cos\frac{A - C}{2} 2 sin B = sin A + sin C ⇒ 4 sin 2 B cos 2 B = 2 sin 2 A + C cos 2 A − C
⇒ 2 cos A + C 2 = cos A − C 2 \Rightarrow 2\cos\frac{A + C}{2} = \cos\frac{A - C}{2} ⇒ 2 cos 2 A + C = cos 2 A − C
L.H.S. = 4 ( 1 − cos A ) ( 1 − cos C ) = 4.2 sin 2 A 2 . 2 sin 2 C 2 = 4(1 - \cos A)(1 - \cos C) = 4.2\sin^2\frac{A}{2}.2\sin^2\frac{C}{2} = 4 ( 1 − cos A ) ( 1 − cos C ) = 4.2 sin 2 2 A .2 sin 2 2 C
4 ( 2 sin A 2 sin C 2 ) 2 = 4 ( cos A − C 2 − cos A + C 2 ) 2 4\left(2\sin\frac{A}{2}\sin\frac{C}{2}\right)^2 = 4\left(\cos\frac{A - C}{2} - \cos\frac{A + C}{2}\right)^2 4 ( 2 sin 2 A sin 2 C ) 2 = 4 ( cos 2 A − C − cos 2 A + C ) 2
= 4 ( 2 cos A + C 2 − cos A + C 2 ) 2 = 4 cos 2 A + C 2 = 4\left(2\cos\frac{A + C}{2} - \cos\frac{A + C}{2}\right)^2 = 4\cos^2\frac{A + C}{2} = 4 ( 2 cos 2 A + C − cos 2 A + C ) 2 = 4 cos 2 2 A + C
R.H.S. = cos A + cos C = 2 cos A + C 2 cos A − C 2 = 4 cos 2 A + C 2 = \cos A + \cos C = 2\cos\frac{A + C}{2}\cos\frac{A - C}{2} = 4\cos^2\frac{A + C}{2} = cos A + cos C = 2 cos 2 A + C cos 2 A − C = 4 cos 2 2 A + C
Thus, L.H.S. = R.H.S.
Given, a , b , c a, b, c a , b , c
⇒ 1 a . 1 b , 1 c \Rightarrow \frac{1}{a}. \frac{1}{b}, \frac{1}{c} ⇒ a 1 . b 1 , c 1
⇒ s a , s b , s c \Rightarrow \frac{s}{a}, \frac{s}{b}, \frac{s}{c} ⇒ a s , b s , c s
⇒ s a − 1 , s b − 1 , s c − 1 \Rightarrow \frac{s}{a} -1, \frac{s}{b} - 1, \frac{s}{c} - 1 ⇒ a s − 1 , b s − 1 , c s − 1
⇒ b c ( s − b ) ( s − c ) , c a ( s − c ) ( s − a ) , a b ( s − a ) ( s − c ) \Rightarrow \frac{bc}{(s - b)(s - c), \frac{ca}{(s - c)(s - a)}}, \frac{ab}{(s - a)(s - c)} ⇒ ( s − b ) ( s − c ) , ( s − c ) ( s − a ) c a b c , ( s − a ) ( s − c ) ab
⇒ 1 sin 2 A 2 , 1 sin 2 B 2 , 1 sin 2 C 2 \Rightarrow \frac{1}{\sin^2\frac{A}{2}}, \frac{1}{\sin^2\frac{B}{2}}, \frac{1}{\sin^2\frac{C}{2}} ⇒ s i n 2 2 A 1 , s i n 2 2 B 1 , s i n 2 2 C 1
⇒ sin 2 A 2 , sin 2 B 2 , sin 2 C 2 \Rightarrow \sin^2\frac{A}{2}, \sin^2\frac{B}{2}, \sin^2\frac{C}{2} ⇒ sin 2 2 A , sin 2 2 B , sin 2 2 C
We have to prove that cos A cot A 2 , cos B cot B 2 , cot C cot C 2 \cos A\cot\frac{A}{2}, \cos B\cot\frac{B}{2}, \cot C\cot\frac{C}{2} cos A cot 2 A , cos B cot 2 B , cot C cot 2 C
⇒ ( 1 − 2 sin 2 A 2 ) cot A 2 ( 1 − 2 sin 2 B 2 ) cot B 2 , ( 1 − 2 sin 2 C 2 ) cot C 2 \Rightarrow \left(1 - 2\sin^2\frac{A}{2}\right)\cot\frac{A}{2} \left(1 - 2\sin^2\frac{B}{2}\right)\cot\frac{B}{2},
\left(1 - 2\sin^2\frac{C}{2}\right)\cot\frac{C}{2} ⇒ ( 1 − 2 sin 2 2 A ) cot 2 A ( 1 − 2 sin 2 2 B ) cot 2 B , ( 1 − 2 sin 2 2 C ) cot 2 C
⇒ cot A 2 − sin A , cot B 2 − sin B , cot C 2 − sin C \Rightarrow \cot\frac{A}{2} - \sin A, \cot\frac{B}{2} - \sin B, \cot\frac{C}{2} - \sin C ⇒ cot 2 A − sin A , cot 2 B − sin B , cot 2 C − sin C
Thus if we prove that cot A 2 , cot B 2 , cot C 2 \cot \frac{A}{2}, \cot \frac{B}{2}, \cot \frac{C}{2} cot 2 A , cot 2 B , cot 2 C sin A , sin B , sin C \sin A, \sin B, \sin C sin A , sin B , sin C
Now, cot A 2 + cot C 2 = s ( s − a ) Δ + s ( s − c ) Δ = s Δ [ 2 s − a − c ] \cot \frac{A}{2} + \cot \frac{C}{2} = \frac{s(s - a)}{\Delta} + \frac{s(s - c)}{\Delta} = \frac{s}{\Delta}[2s -
a - c] cot 2 A + cot 2 C = Δ s ( s − a ) + Δ s ( s − c ) = Δ s [ 2 s − a − c ]
= s Δ ( 2 s − 2 b ) [ ∵ 2 b = a + c ] = 2 cot B 2 = \frac{s}{\Delta}(2s - 2b)[\because 2b = a + c] = 2\cot \frac{B}{2} = Δ s ( 2 s − 2 b ) [ ∵ 2 b = a + c ] = 2 cot 2 B
Thus, cot A 2 , cot B 2 , cot C 2 \cot \frac{A}{2}, \cot \frac{B}{2}, \cot \frac{C}{2} cot 2 A , cot 2 B , cot 2 C
Since a , b , c a, b, c a , b , c
2 b = a + c ⇒ 2 sin B = sin A + sin C 2b = a + c \Rightarrow 2\sin B = \sin A + \sin C 2 b = a + c ⇒ 2 sin B = sin A + sin C
Thus, sin A , sin B , sin C \sin A, \sin B, \sin C sin A , sin B , sin C
Hence the result.
Let the sides be a − d , a , a + d a - d, a, a + d a − d , a , a + d
2 s = 2s = 2 s = = 3 a ∴ s = 3 a 2 = 3a \therefore s = \frac{3a}{2} = 3 a ∴ s = 2 3 a
Now, Δ 1 = \Delta_1 = Δ 1 =
= 3 a 2 ( 3 a 2 − a + d ) ( 3 a 2 − a ) ( 3 a 2 − a − d ) = \sqrt{\frac{3a}{2}\left(\frac{3a}{2} - a + d\right)\left(\frac{3a}{2} - a\right)\left(\frac{3a}{2}- a- d\right)} = 2 3 a ( 2 3 a − a + d ) ( 2 3 a − a ) ( 2 3 a − a − d )
= 3 a 4 ( a + 2 d ) ( a − 2 d ) = 3 a 4 a 2 − 4 d 2 = \frac{\sqrt{3}a}{4}\sqrt{(a + 2d)(a - 2d)} = \frac{\sqrt{3}a}{4}\sqrt{a^2 - 4d^2} = 4 3 a ( a + 2 d ) ( a − 2 d ) = 4 3 a a 2 − 4 d 2
An equilateral triangle with same perimeter will have each side = a = a = a 3 a . 3a. 3 a .
Δ 2 = \Delta_2 = Δ 2 = = 3 4 a 2 = \frac{\sqrt{3}}{4}a^2 = 4 3 a 2
Given, Δ 1 Δ 2 = 3 5 \frac{\Delta_1}{\Delta_2} = \frac{3}{5} Δ 2 Δ 1 = 5 3
⇒ a 2 − 4 d 2 a = 3 5 ⇒ a d = 4 2 [ ∵ d > 0 ] \Rightarrow \frac{\sqrt{a^2 - 4d^2}}{a} = \frac{3}{5} \Rightarrow \frac{a}{d} = \frac{4}{2}[\because d > 0] ⇒ a a 2 − 4 d 2 = 5 3 ⇒ d a = 2 4 [ ∵ d > 0 ]
Ratio of sides = a − d : a : a + d = a d − 1 : a d : a d + 1 = 3 : 5 : 7 = a - d: a: a + d = \frac{a}{d} - 1:\frac{a}{d}:\frac{a}{d}+1 = 3:5:7 = a − d : a : a + d = d a − 1 : d a : d a + 1 = 3 : 5 : 7
Let A B C ABC A BC tan A , tan B , tan C \tan A, \tan B, \tan C tan A , tan B , tan C
∴ tan A − tan B = tan B − tan C \therefore \tan A - \tan B = \tan B - \tan C ∴ tan A − tan B = tan B − tan C
So either both sides are positive or both sides are negative.
If both sides are positive then tan A \tan A tan A tan A \tan A tan A
According to question x x x ⇒ tan A = x \Rightarrow \tan A = x ⇒ tan A = x
⇒ sin 2 x = x 2 1 + x 2 \Rightarrow \sin^2x = \frac{x^2}{1 + x^2} ⇒ sin 2 x = 1 + x 2 x 2
Now, 2 tan B = tan A + tan C ⇒ tan B = x + tan C 2 2\tan B = \tan A + \tan C \Rightarrow \tan B = \frac{x + \tan C}{2} 2 tan B = tan A + tan C ⇒ tan B = 2 x + t a n C
B = π − ( A + C ) B = \pi - (A + C) B = π − ( A + C )
⇒ tan B = − tan ( A + C ) = − x + tan C 1 − x tan C \Rightarrow \tan B = -\tan(A + C) = -\frac{x + \tan C}{1 - x\tan C} ⇒ tan B = − tan ( A + C ) = − 1 − x t a n C x + t a n C
Thus, x + tan C 2 = − x + tan C 1 − x tan C \frac{x + \tan C}{2} = -\frac{x + \tan C}{1 - x\tan C} 2 x + t a n C = − 1 − x t a n C x + t a n C
⇒ 1 − x tan C = − 2 ⇒ tan C = 3 x \Rightarrow 1 - x\tan C = -2 \Rightarrow \tan C = \frac{3}{x} ⇒ 1 − x tan C = − 2 ⇒ tan C = x 3
sin 2 C = 9 9 + x 2 \sin^2C = \frac{9}{9 + x^2} sin 2 C = 9 + x 2 9
⇒ tan B = x 2 + 3 2 x ⇒ sin 2 B = ( x 2 + 3 ) 2 ( x 2 + 1 ) ( x 2 + 9 ) \Rightarrow \tan B = \frac{x^2 + 3}{2x} \Rightarrow \sin^2B = \frac{(x^2 + 3)^2}{(x^2 + 1)(x^2 + 9)} ⇒ tan B = 2 x x 2 + 3 ⇒ sin 2 B = ( x 2 + 1 ) ( x 2 + 9 ) ( x 2 + 3 ) 2
Now a 2 : b 2 : c 2 = sin 2 A : sin 2 B : sin 2 C a^2:b^2:c^2 = \sin^2A:\sin^2B:\sin^2C a 2 : b 2 : c 2 = sin 2 A : sin 2 B : sin 2 C
Hence the result.
Let the sides be a − d , a , a + d . a - d, a, a + d. a − d , a , a + d . d > 0 , d > 0, d > 0 , a + d a + d a + d a − d . a -
d. a − d .
Hence angle A A A C C C ∠ A = θ ∴ C = θ + α ⇒ B = π − 2 θ − α \angle A = \theta \therefore C =
\theta + \alpha \Rightarrow B = \pi - 2\theta - \alpha ∠ A = θ ∴ C = θ + α ⇒ B = π − 2 θ − α
Applying sine rule, we get
a − d sin θ = a sin [ π − ( 2 θ + α ) ] = a + d sin ( θ + α ) = 2 a sin θ + sin ( θ + α ) \frac{a - d}{\sin\theta} = \frac{a}{\sin[\pi - (2\theta + \alpha)]} = \frac{a + d}{\sin(\theta + \alpha)} =
\frac{2a}{\sin\theta + \sin(\theta + \alpha)} s i n θ a − d = s i n [ π − ( 2 θ + α )] a = s i n ( θ + α ) a + d = s i n θ + s i n ( θ + α ) 2 a
a − d sin θ = a + d sin ( θ + α ) \frac{a - d}{\sin\theta} = \frac{a + d}{\sin(\theta + \alpha)} s i n θ a − d = s i n ( θ + α ) a + d
⇒ a − d a + d = sin θ sin ( θ + α ) \Rightarrow \frac{a - d}{a + d} = \frac{\sin\theta}{\sin(\theta + \alpha)} ⇒ a + d a − d = s i n ( θ + α ) s i n θ
By componendo and dividendo, we get
2 a 2 d = sin θ + sin ( θ + α ) sin ( θ + α ) − sin θ \frac{2a}{2d} = \frac{\sin\theta + \sin(\theta + \alpha)}{\sin(\theta + \alpha) - \sin\theta} 2 d 2 a = s i n ( θ + α ) − s i n θ s i n θ + s i n ( θ + α )
⇒ d a = tan α 2 tan ( θ + α 2 ) \Rightarrow \frac{d}{a} = \frac{\tan\frac{\alpha}{2}}{\tan\left(\theta + \frac{\alpha}{2}\right)} ⇒ a d = t a n ( θ + 2 α ) t a n 2 α
Now a sin ( 2 θ + α ) = 2 a sin θ + sin ( θ + α ) \frac{a}{\sin(2\theta + \alpha)} = \frac{2a}{\sin\theta + \sin(\theta + \alpha)} s i n ( 2 θ + α ) a = s i n θ + s i n ( θ + α ) 2 a
⇒ 1 2 = cos ( θ + α 2 ) cos α 2 \Rightarrow \frac{1}{2} = \frac{\cos\left(\theta + \frac{\alpha}{2}\right)}{\cos\frac{\alpha}{2}} ⇒ 2 1 = c o s 2 α c o s ( θ + 2 α )
cos ( θ + α 2 ) = cos α 2 2 \cos\left(\theta + \frac{\alpha}{2}\right) = \frac{\cos\frac{\alpha}{2}}{2} cos ( θ + 2 α ) = 2 c o s 2 α
tan ( θ + α 2 ) = 4 − cos 2 α 2 cos α 2 \tan\left(\theta + \frac{\alpha}{2}\right) = \frac{\sqrt{4 - \cos^2\frac{\alpha}{2}}}{\cos\frac{\alpha}{2}} tan ( θ + 2 α ) = c o s 2 α 4 − c o s 2 2 α
d a = 1 − cos α 7 − cos α = x \frac{d}{a} = \sqrt{\frac{1 - \cos\alpha}{7 - \cos\alpha}} = x a d = 7 − c o s α 1 − c o s α = x
Thus, required ratio = a − d : a : a + d = 1 − x : 1 : 1 + x = a - d:a:a + d = 1 - x: 1: 1 + x = a − d : a : a + d = 1 − x : 1 : 1 + x
Consider that sides of the triangle are a , a r , a r 2 a, ar, ar^2 a , a r , a r 2 a r 2 ar^2 a r 2
∵ a r 2 < a + a r ⇒ r 2 − r − 1 < 0 \because ar^2 < a + ar \Rightarrow r^2 -r - 1 < 0 ∵ a r 2 < a + a r ⇒ r 2 − r − 1 < 0
( r − 1 2 ) − 5 4 < 0 ⇒ ( r − 1 2 ) 2 < 5 4 \left(r - \frac{1}{2}\right) - \frac{5}{4} < 0 \Rightarrow \left(r - \frac{1}{2}\right)^2 < \frac{5}{4} ( r − 2 1 ) − 4 5 < 0 ⇒ ( r − 2 1 ) 2 < 4 5
r − 1 2 < 5 2 ∴ r < 1 2 ( 5 + 1 ) r - \frac{1}{2} < \frac{\sqrt{5}}{2} \therefore r < \frac{1}{2}(\sqrt{5} + 1) r − 2 1 < 2 5 ∴ r < 2 1 ( 5 + 1 )
r 2 < 1 2 ( 3 + 5 ) r^2 < \frac{1}{2}(3 + \sqrt{5}) r 2 < 2 1 ( 3 + 5 )
r 4 < 1 2 ( 7 + 3 5 ) r^4 < \frac{1}{2}(7 + 3\sqrt{5}) r 4 < 2 1 ( 7 + 3 5 )
1 + r 2 − r 4 < − 1 − 5 1 + r^2 - r^4 < - 1 - \sqrt{5} 1 + r 2 − r 4 < − 1 − 5
∴ 1 + r 2 − r 4 < r \therefore 1 + r^2 - r^4 < r ∴ 1 + r 2 − r 4 < r
∴ cos C = a 2 + a 2 r 2 − a 2 r 4 2 a 2 r < 1 2 \therefore \cos C = \frac{a^2 + a^2r^2 - a^2r^4}{2a^2r} < \frac{1}{2} ∴ cos C = 2 a 2 r a 2 + a 2 r 2 − a 2 r 4 < 2 1
cos C < cos π 3 ∴ C > π 3 \cos C < \cos \frac{\pi}{3} \therefore C > \frac{\pi}{3} cos C < cos 3 π ∴ C > 3 π
cos B = 1 + r 4 − r 2 2 r 2 = 1 2 [ ( r − 1 3 ) 2 + 1 ] > 1 2 \cos B = \frac{1 + r^4 - r^2}{2r^2} = \frac{1}{2}\left[\left(r - \frac{1}{3}\right)^2 + 1\right] > \frac{1}{2} cos B = 2 r 2 1 + r 4 − r 2 = 2 1 [ ( r − 3 1 ) 2 + 1 ] > 2 1
∴ cos B > cos π 3 ∴ B < π 3 \therefore \cos B > \cos\frac{\pi}{3} \therefore B < \frac{\pi}{3} ∴ cos B > cos 3 π ∴ B < 3 π
∵ a < a r < a r 2 ∴ A > B > C \because a < ar <ar^2 \therefore A > B > C ∵ a < a r < a r 2 ∴ A > B > C
Hence A < B < π 3 < C A < B < \frac{\pi}{3} < C A < B < 3 π < C
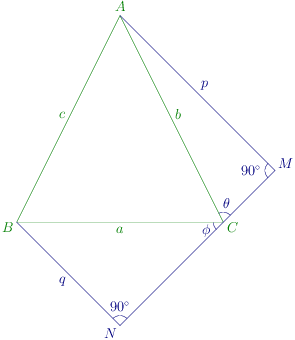
The diagram is given below:
We are given A M = p , B N = q AM = p, BN = q A M = p , BN = q
Let ∠ A C M = θ \angle ACM = \theta ∠ A CM = θ ∠ B C N = ϕ \angle BCN = \phi ∠ BCN = ϕ
Then, sin θ = p b \sin\theta = \frac{p}{b} sin θ = b p sin ϕ = q a \sin\phi = \frac{q}{a} sin ϕ = a q
Now C = π − ( θ + ϕ ) C = \pi - (\theta + \phi) C = π − ( θ + ϕ )
cos C = − cos ( θ + ϕ ) = sin θ sin ϕ − cos θ cos ϕ \cos C = -\cos(\theta + \phi) = \sin\theta\sin\phi -\cos\theta\cos\phi cos C = − cos ( θ + ϕ ) = sin θ sin ϕ − cos θ cos ϕ
⇒ 1 − p 2 b 2 1 − q 2 a 2 = p q a b − cos C \Rightarrow \sqrt{1 - \frac{p^2}{b^2}}\sqrt{1 - \frac{q^2}{a^2}} = \frac{pq}{ab} - \cos C ⇒ 1 − b 2 p 2 1 − a 2 q 2 = ab pq − cos C
Squaring, we get
( 1 − p 2 q 2 ) ( 1 − q 2 a 2 ) = p 2 q 2 a 2 b 2 − 2 p q a b cos C + cos 2 C \left(1 - \frac{p^2}{q^2}\right)\left(1 - \frac{q^2}{a^2}\right) = \frac{p^2q^2}{a^2b^2} - 2\frac{pq}{ab}\cos C +
\cos^2C ( 1 − q 2 p 2 ) ( 1 − a 2 q 2 ) = a 2 b 2 p 2 q 2 − 2 ab pq cos C + cos 2 C
a 2 b 2 + b 2 q 2 − 2 a b p q cos C = a 2 b 2 sin 2 C a^2b^2 + b^2q^2 - 2abpq\cos C = a^2b^2\sin^2C a 2 b 2 + b 2 q 2 − 2 ab pq cos C = a 2 b 2 sin 2 C
∠ O C B = θ , ∠ B O C = π − θ − ( C − θ ) = π − C \angle OCB = \theta, \angle BOC = \pi - \theta - (C - \theta) = \pi - C ∠ OCB = θ , ∠ BOC = π − θ − ( C − θ ) = π − C
Similarly, ∠ A O B = π − B \angle AOB = \pi - B ∠ A OB = π − B
From △ A O B , \triangle AOB, △ A OB ,
O B sin θ = A B sin ( π − B ) = c sin B ⇒ O B = c sin θ sin B \frac{OB}{\sin\theta} = \frac{AB}{\sin(\pi - B)} = \frac{c}{\sin B} \Rightarrow OB = \frac{c\sin\theta}{\sin B} s i n θ OB = s i n ( π − B ) A B = s i n B c ⇒ OB = s i n B c s i n θ
Again from △ O B C , \triangle OBC, △ OBC ,
O B sin ( C − θ ) = B C sin ( π − C ) = a sin C ⇒ O B = a sin ( C − θ ) sin C \frac{OB}{\sin(C - \theta)} = \frac{BC}{\sin(\pi - C)} = \frac{a}{\sin C} \Rightarrow OB = \frac{a\sin(C -
\theta)}{\sin C} s i n ( C − θ ) OB = s i n ( π − C ) BC = s i n C a ⇒ OB = s i n C a s i n ( C − θ )
⇒ c sin θ sin B = a sin ( C − θ ) sin C \Rightarrow \frac{c\sin\theta}{\sin B} = \frac{a\sin(C - \theta)}{\sin C} ⇒ s i n B c s i n θ = s i n C a s i n ( C − θ )
⇒ sin C sin θ sin C = sin A sin ( C − θ ) sin B \Rightarrow \sin C\sin\theta\sin C = \sin A\sin(C - \theta)\sin B ⇒ sin C sin θ sin C = sin A sin ( C − θ ) sin B
⇒ sin C sin θ sin ( A + B ) = sin A sin B sin ( C − θ ) \Rightarrow \sin C\sin\theta\sin(A + B) = \sin A\sin B\sin(C - \theta) ⇒ sin C sin θ sin ( A + B ) = sin A sin B sin ( C − θ )
⇒ sin C sin θ sin A cos B + sin C sin θ cos A sin B = sin A sin B sin C cos θ − sin A sin B cos C sin θ \Rightarrow \sin C\sin\theta\sin A\cos B + \sin C\sin\theta\cos A\sin B = \sin A\sin B\sin C\cos\theta - \sin A\sin
B\cos C\sin\theta ⇒ sin C sin θ sin A cos B + sin C sin θ cos A sin B = sin A sin B sin C cos θ − sin A sin B cos C sin θ
Dividing by sin A sin B sin C sin θ , \sin A\sin B\sin C\sin\theta, sin A sin B sin C sin θ ,
⇒ cot B + cot A = cot θ − cot C \Rightarrow \cot B + \cot A = \cot \theta - \cot C ⇒ cot B + cot A = cot θ − cot C
cot θ = cot A + cot B + cot C \cot\theta = \cot A + \cot B + \cot C cot θ = cot A + cot B + cot C
In a triangle cot A cot B + cot B cot C + cot C cot A = 1 \cot A\cot B + \cot B\cot C + \cot C\cot A = 1 cot A cot B + cot B cot C + cot C cot A = 1
Thus, squaaring we get
cosec 2 θ = cosec 2 A + cosec 2 B + cosec 2 C \cosec^2\theta = \cosec^2A + \cosec^2B + \cosec^2C cosec 2 θ = cosec 2 A + cosec 2 B + cosec 2 C
The diagram is given below:
Let O O O O P = x . OP = x. OP = x . B P = a 2 . BP= \frac{a}{2}. BP = 2 a .
Angle made at center will be double that made at perimeter, thus
tan A = a 2 x \tan A = \frac{a}{2x} tan A = 2 x a
Similarly, tan B = b 2 y , tan C = c 2 z \tan B = \frac{b}{2y}, \tan C = \frac{c}{2z} tan B = 2 y b , tan C = 2 z c
In a △ A B C , \triangle ABC, △ A BC ,
tan A + tan B + tan C = tan A tan B tan C \tan A + \tan B + \tan C = \tan A\tan B\tan C tan A + tan B + tan C = tan A tan B tan C
⇒ a x + b y + c z = a b c 4 x y z \Rightarrow \frac{a}{x} + \frac{b}{y} + \frac{c}{z} = \frac{abc}{4xyz} ⇒ x a + y b + z c = 4 x yz ab c
Given, B D m = D C n = B C m + n \frac{BD}{m} = \frac{DC}{n} = \frac{BC}{m + n} m B D = n D C = m + n BC
⇒ B D = m a m + n \Rightarrow BD = \frac{ma}{m + n} ⇒ B D = m + n ma
In △ A B D , \triangle ABD, △ A B D ,
x 2 = A B 2 + B D 2 − 2 A B . B D . cos B = c 2 + m 2 a 2 ( m + n ) 2 − 2. c . m a m + n . c 2 + a 2 − b 2 2 c a x^2 = AB^2 + BD^2 - 2AB.BD.\cos B = c^2 + \frac{m^2a^2}{(m + n)^2} - 2.c.\frac{ma}{m + n}.\frac{c^2 + a^2 - b^2}{2ca} x 2 = A B 2 + B D 2 − 2 A B . B D . cos B = c 2 + ( m + n ) 2 m 2 a 2 − 2. c . m + n ma . 2 c a c 2 + a 2 − b 2
Hence the result.
Given, sin A + sin B + sin C = 3 3 2 \sin A + \sin B + \sin C = \frac{3\sqrt{3}}{2} sin A + sin B + sin C = 2 3 3
⇒ cos A 2 cos B 2 cos C 2 = ( 3 2 ) 3 \Rightarrow \cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2} = \left(\frac{\sqrt{3}}{2}\right)^3 ⇒ cos 2 A cos 2 B cos 2 C = ( 2 3 ) 3
Under the constraint A + B + C = π A + B + C = \pi A + B + C = π A = B = C = π 3 A = B = C = \frac{\pi}{3} A = B = C = 3 π
If A = B = C A = B = C A = B = C
cos A 2 cos B 2 cos C 2 = cos 3 3 0 ∘ = ( 3 2 ) 3 \cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2} = \cos^330^\circ = \left(\frac{\sqrt{3}}{2}\right)^3 cos 2 A cos 2 B cos 2 C = cos 3 3 0 ∘ = ( 2 3 ) 3
Thus, the triangle is equilateral.
This problem can be solved like previous problem.
Given, cos A + 2 cos B + cos C = 2 \cos A + 2\cos B + \cos C = 2 cos A + 2 cos B + cos C = 2
cos A + cos C = 2 ( 1 − cos B ) ⇒ 2 cos A + C 2 cos A − C 2 = 2.2 sin 2 B 2 \cos A + \cos C = 2(1 - \cos B) \Rightarrow 2\cos\frac{A + C}{2}\cos\frac{A - C}{2} = 2.2\sin^2\frac{B}{2} cos A + cos C = 2 ( 1 − cos B ) ⇒ 2 cos 2 A + C cos 2 A − C = 2.2 sin 2 2 B
cos A − C 2 = 2. cos A + C 2 \cos\frac{A - C}{2} = 2.\cos\frac{A + C}{2} cos 2 A − C = 2. cos 2 A + C
2 sin A + C 2 cos A − C 2 = 2.2 sin A + C 2 cos A + C 2 2\sin\frac{A + C}{2}\cos\frac{A - C}{2} = 2.2\sin\frac{A + C}{2}\cos\frac{A + C}{2} 2 sin 2 A + C cos 2 A − C = 2.2 sin 2 A + C cos 2 A + C
sin A + sin C = 2. sin ( A + C ) = 2 sin B ⇒ a + c = 2 b \sin A + \sin C = 2.\sin(A + C) = 2\sin B \Rightarrow a + c = 2b sin A + sin C = 2. sin ( A + C ) = 2 sin B ⇒ a + c = 2 b
Thus, the sides are in a , b , c . a,b,c. a , b , c .
tan A 2 + tan C 2 = ( s − b ) ( s − c ) s ( s − a ) + ( s − a ) ( s − b ) s ( s − c ) \tan\frac{A}{2} + \tan\frac{C}{2} = \sqrt{\frac{(s - b)(s - c)}{s(s - a)}} + \sqrt{\frac{(s - a)(s - b)}{s(s - c)}} tan 2 A + tan 2 C = s ( s − a ) ( s − b ) ( s − c ) + s ( s − c ) ( s − a ) ( s − b )
= s − b s ( s − c s − a + s − a s − c ) = \sqrt{\frac{s - b}{s}}\left(\sqrt{\frac{s - c}{s - a}} + \sqrt{\frac{s - a}{s - c}}\right) = s s − b ( s − a s − c + s − c s − a )
= s − b s ( s − c + s − a ( s − a ) ( s − c ) ) = \sqrt{\frac{s - b}{s}} \left(\frac{s - c + s - a}{\sqrt{(s - a)(s - c)}}\right) = s s − b ( ( s − a ) ( s − c ) s − c + s − a )
= b s s ( s − b ) ( s − a ) ( s − c ) = b s cot B 2 = \frac{b}{s}\sqrt{\frac{s(s - b)}{(s - a)(s - c)}} = \frac{b}{s}\cot\frac{B}{2} = s b ( s − a ) ( s − c ) s ( s − b ) = s b cot 2 B
Since sides are in A.P. 2 b = a + c ⇒ 2 s = 3 b 2b = a + c \Rightarrow 2s = 3b 2 b = a + c ⇒ 2 s = 3 b
tan A 2 + tan C 2 = 2 3 cot B 2 \tan\frac{A}{2} + \tan\frac{C}{2} = \frac{2}{3}\cot\frac{B}{2} tan 2 A + tan 2 C = 3 2 cot 2 B
Given, a − b b − c = s − a s − c \frac{a - b}{b - c} = \frac{s - a}{s - c} b − c a − b = s − c s − a
⇒ s − a a − b = s − c b − c \Rightarrow \frac{s - a}{a - b} = \frac{s - c}{b - c} ⇒ a − b s − a = b − c s − c
⇒ s − a ( s − b ) − ( s − a ) = s − c ( s − c ) − ( s − b ) \Rightarrow \frac{s - a}{(s - b) - (s - a)} = \frac{s - c}{(s - c) - (s - b)} ⇒ ( s − b ) − ( s − a ) s − a = ( s − c ) − ( s − b ) s − c
⇒ Δ r 1 Δ r 2 − Δ r 1 = Δ r 3 Δ r 3 − Δ r 2 \Rightarrow \frac{\frac{\Delta}{r_1}}{\frac{\Delta}{r_2} - \frac{\Delta}{r_1}} =
\frac{\frac{\Delta}{r_3}}{\frac{\Delta}{r_3} - \frac{\Delta}{r_2}} ⇒ r 2 Δ − r 1 Δ r 1 Δ = r 3 Δ − r 2 Δ r 3 Δ
⇒ 2 r 2 = r 1 + r 3 \Rightarrow 2r_2 = r_1 + r_3 ⇒ 2 r 2 = r 1 + r 3
Hence the result.
Let the sides be a , a r , a r 2 . a, ar, ar^2. a , a r , a r 2 .
x = ( b 2 − c 2 ) tan B + tan C tan B − tan C = ( b 2 − c 2 ) sin B cos C + cos B sin C sin B cos C − cos B sin C x = (b^2 - c^2)\frac{\tan B + \tan C}{\tan B - \tan C} = (b^2 - c^2)\frac{\sin B\cos C + \cos B\sin C}{\sin B\cos C -
\cos B\sin C} x = ( b 2 − c 2 ) t a n B − t a n C t a n B + t a n C = ( b 2 − c 2 ) s i n B c o s C − c o s B s i n C s i n B c o s C + c o s B s i n C
= ( b 2 − c 2 ) sin ( B + C ) sin ( B − C ) = 4 R 2 ( sin 2 B − sin 2 C ) sin 2 ( B + C ) sin 2 B − sin 2 C = (b^2 - c^2)\frac{\sin(B + C)}{\sin(B - C)} = 4R^2(\sin^2B - \sin^2C)\frac{\sin^2(B + C)}{\sin^2B - \sin^2C} = ( b 2 − c 2 ) s i n ( B − C ) s i n ( B + C ) = 4 R 2 ( sin 2 B − sin 2 C ) s i n 2 B − s i n 2 C s i n 2 ( B + C )
= a 2 = a^2 = a 2
Similalry, y = a 2 r 2 y = a^2r^2 y = a 2 r 2 z = a 2 r 4 z = a^2r^4 z = a 2 r 4
Thus, x , y , z x,y,z x , y , z
Given, r 1 , r 2 , r 3 r_1,r_2,r_3 r 1 , r 2 , r 3
⇒ 1 r 1 , 1 r 2 , 1 r 3 \Rightarrow \frac{1}{r_1}, \frac{1}{r_2}, \frac{1}{r_3} ⇒ r 1 1 , r 2 1 , r 3 1
⇒ 1 r 2 − 1 r 1 = 1 r 3 − 1 r 2 \Rightarrow \frac{1}{r_2} - \frac{1}{r_1} = \frac{1}{r_3}- \frac{1}{r_2} ⇒ r 2 1 − r 1 1 = r 3 1 − r 2 1
⇒ s − b Δ − s − a Δ = s − c Δ − s − b Δ \Rightarrow \frac{s - b}{\Delta} - \frac{s - a}{\Delta} = \frac{s - c}{\Delta} - \frac{s - b}{\Delta} ⇒ Δ s − b − Δ s − a = Δ s − c − Δ s − b
⇒ s − b − s + a = s − c − s + b \Rightarrow s - b - s + a = s - c - s + b ⇒ s − b − s + a = s − c − s + b
⇒ a − b = b − c \Rightarrow a - b = b - c ⇒ a − b = b − c
Hence a , b , c a,b,c a , b , c
Given, r 1 = r 2 + r 3 + r ⇒ r 1 − r = r 2 + r 3 r_1 = r_2 + r_3 + r \Rightarrow r_1 - r = r_2 + r_3 r 1 = r 2 + r 3 + r ⇒ r 1 − r = r 2 + r 3
⇒ Δ s − a − Δ s = Δ s − b + Δ s − c \Rightarrow \frac{\Delta}{s - a} - \frac{\Delta}{s} = \frac{\Delta}{s - b} + \frac{\Delta}{s - c} ⇒ s − a Δ − s Δ = s − b Δ + s − c Δ
⇒ a s ( s − a ) = a ( s − b ) ( s − c ) \Rightarrow \frac{a}{s(s - a)} = \frac{a}{(s - b)(s - c)} ⇒ s ( s − a ) a = ( s − b ) ( s − c ) a
⇒ s ( s − a ) = ( s − b ) ( s − c ) \Rightarrow s(s - a) = (s - b)(s - c) ⇒ s ( s − a ) = ( s − b ) ( s − c )
⇒ s ( b + c − a ) = b c \Rightarrow s(b + c - a) = bc ⇒ s ( b + c − a ) = b c
⇒ b + c − a 2 ( b + c − a ) = b c \Rightarrow \frac{b + c - a}{2}(b + c - a) = bc ⇒ 2 b + c − a ( b + c − a ) = b c
⇒ ( b + c ) 2 − a 2 = 2 b c \Rightarrow (b + c)^2 - a^2 = 2bc ⇒ ( b + c ) 2 − a 2 = 2 b c
⇒ b 2 + c 2 = a 2 \Rightarrow b^2 + c^2 = a^2 ⇒ b 2 + c 2 = a 2
Thus, the triangle is right angled.
R.H.S. = 1 + r R = 1 + Δ s a b c 4 Δ = 1 + 4 Δ 2 a b c s = 1 + \frac{r}{R} = 1 + \frac{\frac{\Delta}{s}}{\frac{abc}{4\Delta}} = 1 + \frac{4\Delta^2}{abcs} = 1 + R r = 1 + 4Δ ab c s Δ = 1 + ab cs 4 Δ 2
L.H.S. = cos A + cos B + cos C = 2 cos A + B 2 cos A − B 2 + cos C = \cos A + \cos B + \cos C = 2\cos\frac{A + B}{2}\cos\frac{A - B}{2} + \cos C = cos A + cos B + cos C = 2 cos 2 A + B cos 2 A − B + cos C
= 2 sin C 2 cos A − B 2 + 1 − 2 sin 2 C 2 = 2\sin\frac{C}{2}\cos\frac{A - B}{2} + 1 - 2\sin^2\frac{C}{2} = 2 sin 2 C cos 2 A − B + 1 − 2 sin 2 2 C
= 1 + 2 sin C 2 [ cos A − B 2 − sin C 2 ] = 1 + 2\sin\frac{C}{2}\left[\cos\frac{A - B}{2} - \sin\frac{C}{2}\right] = 1 + 2 sin 2 C [ cos 2 A − B − sin 2 C ]
= 1 + 2 sin C 2 [ cos A − B 2 − cos A + B 2 ] = 1 + 2\sin\frac{C}{2}\left[\cos\frac{A - B}{2} - \cos\frac{A + B}{2}\right] = 1 + 2 sin 2 C [ cos 2 A − B − cos 2 A + B ]
= 1 + 4 sin A 2 sin B 2 sin C 2 = 1 + 4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2} = 1 + 4 sin 2 A sin 2 B sin 2 C
= 1 + 4 ( s − b ) ( s − c ) b c ( s − a ) ( s − c ) c a ( s − a ) ( s − b ) a b = 1 + 4\sqrt{\frac{(s - b)(s - c)}{bc}}\sqrt{\frac{(s - a)(s - c)}{ca}}\sqrt{\frac{(s - a)(s - b)}{ab}} = 1 + 4 b c ( s − b ) ( s − c ) c a ( s − a ) ( s − c ) ab ( s − a ) ( s − b )
= 1 + 4 ( s − a ) ( s − b ) ( s − c ) a b c . s s = 1 + 4\frac{(s - a)(s - b)(s - c)}{abc}.\frac{s}{s} = 1 + 4 ab c ( s − a ) ( s − b ) ( s − c ) . s s
= 1 + 4 Δ 2 a b c s = 1 + 4\frac{\Delta^2}{abcs} = 1 + 4 ab cs Δ 2
Thus, L.H.S. = R.H.S.
Let r 1 , r 2 , r 3 r_1, r_2, r_3 r 1 , r 2 , r 3 A B C , ABC, A BC , r 1 , r 2 , r 3 r_1, r_2, r_3 r 1 , r 2 , r 3
x 3 − ( r 1 + r 2 + r 3 ) x 2 + ( r 1 r 2 + r 2 r 3 + r 3 r 1 ) x − r 1 r 2 r 3 = 0 x^3 - (r_1 + r_2 + r_3)x^2 + (r_1r_2 + r_2r_3 + r_3r_1)x - r_1r_2r_3 = 0 x 3 − ( r 1 + r 2 + r 3 ) x 2 + ( r 1 r 2 + r 2 r 3 + r 3 r 1 ) x − r 1 r 2 r 3 = 0
Now, r 1 + r 2 + r 3 = Δ s − a + Δ s − b + Δ s − c r_1 + r_2 + r_3 = \frac{\Delta}{s - a} + \frac{\Delta}{s - b} + \frac{\Delta}{s - c} r 1 + r 2 + r 3 = s − a Δ + s − b Δ + s − c Δ
= Δ [ 1 s − a + 1 s − b ] + Δ s − c − Δ s + Δ s = \Delta\left[\frac{1}{s - a} + \frac{1}{s - b}\right] + \frac{\Delta}{s - c} - \frac{\Delta}{s} + \frac{\Delta}{s} = Δ [ s − a 1 + s − b 1 ] + s − c Δ − s Δ + s Δ
= Δ [ s − b + s − a ( s − a ) ( s − b ) ] + Δ ( s − s + c ) s ( s − c ) + Δ s = \Delta\left[\frac{s - b + s - a}{(s - a)(s - b)}\right] + \frac{\Delta(s - s + c)}{s(s - c)} + \frac{\Delta}{s} = Δ [ ( s − a ) ( s − b ) s − b + s − a ] + s ( s − c ) Δ ( s − s + c ) + s Δ
= Δ . c ( s − a ) ( s − b ) + Δ . c s ( s − c ) + Δ s = \frac{\Delta.c}{(s - a)(s - b)} + \frac{\Delta.c}{s(s - c)} + \frac{\Delta}{s} = ( s − a ) ( s − b ) Δ. c + s ( s − c ) Δ. c + s Δ
= Δ . c [ s 2 − c s + s 2 − a s − b s + a b s ( s − a ) ( s − b ) ( s − c ) ] + Δ s = \Delta.c\left[\frac{s^2 - cs + s^2 - as - bs + ab}{s(s - a)(s - b)(s - c)}\right] + \frac{\Delta}{s} = Δ. c [ s ( s − a ) ( s − b ) ( s − c ) s 2 − cs + s 2 − a s − b s + ab ] + s Δ
= a b c Δ + Δ s = r + 4 R = \frac{abc}{\Delta} + \frac{\Delta}{s} = r + 4R = Δ ab c + s Δ = r + 4 R
Now, r 1 r 2 + r 2 r 3 + r 3 r 1 = Δ 2 [ s − c + s − a + s − b ( s − a ) ( s − b ) ( s − c ) ] r_1r_2 + r_2r_3 + r_3r_1 = \Delta^2\left[\frac{s - c + s - a + s - b}{(s - a)(s - b)(s - c)}\right] r 1 r 2 + r 2 r 3 + r 3 r 1 = Δ 2 [ ( s − a ) ( s − b ) ( s − c ) s − c + s − a + s − b ]
= Δ 2 . s ( s − a ) ( s − b ) ( s − c ) = s 2 = \frac{\Delta^2.s}{(s - a)(s - b)(s - c)} = s^2 = ( s − a ) ( s − b ) ( s − c ) Δ 2 . s = s 2
r 1 r 2 r 3 = Δ 3 . s s ( s − a ) ( s − b ) ( s − c ) = Δ . s = r s 2 r_1r_2r_3 = \frac{\Delta^3.s}{s(s - a)(s - b)(s - c)} = \Delta.s = rs^2 r 1 r 2 r 3 = s ( s − a ) ( s − b ) ( s − c ) Δ 3 . s = Δ. s = r s 2
Thus, r 1 , r 2 , r 3 r_1, r_2, r_3 r 1 , r 2 , r 3
x 3 − ( r + 4 R ) x 2 + s 2 x − r s 2 = 0 x^3 - (r + 4R)x^2 + s^2x - rs^2 = 0 x 3 − ( r + 4 R ) x 2 + s 2 x − r s 2 = 0
Let s s s s = 12 s = 12 s = 12 Δ = 24 \Delta = 24 Δ = 24
Let a , b , c a,b,c a , b , c
r 1 = Δ s − a = 24 12 − a r_1 = \frac{\Delta}{s - a} = \frac{24}{12 - a} r 1 = s − a Δ = 12 − a 24
r 2 = Δ s − b = 24 12 − b r_2 = \frac{\Delta}{s - b} = \frac{24}{12 - b} r 2 = s − b Δ = 12 − b 24
r 3 = Δ s − c = 24 12 − c r_3 = \frac{\Delta}{s - c} = \frac{24}{12 - c} r 3 = s − c Δ = 12 − c 24
Given r 1 , r 2 , r 3 r_1, r_2, r_3 r 1 , r 2 , r 3
∴ 1 r 2 − 1 r 1 = 1 r 3 − 1 r 2 \therefore \frac{1}{r_2} - \frac{1}{r_1} = \frac{1}{r_3} - \frac{1}{r_2} ∴ r 2 1 − r 1 1 = r 3 1 − r 2 1
⇒ 12 − b 24 − 12 − a 24 = 12 − c 24 − 12 − b 24 \Rightarrow \frac{12 - b}{24} - \frac{12 - a}{24} = \frac{12 - c}{24} - \frac{12 - b}{24} ⇒ 24 12 − b − 24 12 − a = 24 12 − c − 24 12 − b
⇒ a − b = b − c ⇒ 2 b = a + c \Rightarrow a - b = b - c \Rightarrow 2b = a + c ⇒ a − b = b − c ⇒ 2 b = a + c
a + b + c = 24 ⇒ b = 8 a + b + c = 24 \Rightarrow b = 8 a + b + c = 24 ⇒ b = 8
a + c = 16 ⇒ c = 16 − a a + c = 16 \Rightarrow c = 16 - a a + c = 16 ⇒ c = 16 − a
Now, Δ = s ( s − a ) ( s − b ) ( s − c ) ⇒ 24.24 = 12 ( 12 − a ) ( 12 − b ) ( 12 − c ) \Delta = \sqrt{s(s - a)(s - b)(s - c)} \Rightarrow 24.24 = 12(12 - a)(12 - b)(12 - c) Δ = s ( s − a ) ( s − b ) ( s − c ) ⇒ 24.24 = 12 ( 12 − a ) ( 12 − b ) ( 12 − c )
⇒ a 2 − 16 a + 60 = 0 ⇒ a = 6 , 10 ⇒ c = 10 , 6 \Rightarrow a^2 - 16 a + 60 = 0 \Rightarrow a = 6, 10 \Rightarrow c = 10, 6 ⇒ a 2 − 16 a + 60 = 0 ⇒ a = 6 , 10 ⇒ c = 10 , 6
a sin A = b sin B = c sin C = 2 R \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R s i n A a = s i n B b = s i n C c = 2 R
Given, 8 R 2 = a 2 + b 2 + c 2 = 4 R 2 ( sin 2 A + sin 2 B + sin 2 C ) 8R^2 = a^2 + b^2 + c^2 = 4R^2(\sin^2A + \sin^2B + \sin^2C) 8 R 2 = a 2 + b 2 + c 2 = 4 R 2 ( sin 2 A + sin 2 B + sin 2 C )
⇒ ( 1 − sin 2 A ) + ( 1 − sin 2 B ) − sin 2 C = 0 \Rightarrow (1 - \sin^2A) + (1 - \sin^2B) - \sin^2C = 0 ⇒ ( 1 − sin 2 A ) + ( 1 − sin 2 B ) − sin 2 C = 0
⇒ cos 2 A + cos 2 B − sin 2 C = 0 \Rightarrow \cos^2A + \cos^2B - \sin^2C = 0 ⇒ cos 2 A + cos 2 B − sin 2 C = 0
⇒ cos 2 A + cos ( B + C ) cos ( B − C ) = 0 \Rightarrow \cos^2A + \cos(B + C)\cos(B - C) = 0 ⇒ cos 2 A + cos ( B + C ) cos ( B − C ) = 0
⇒ cos A [ cos A − cos ( B − C ) ] = 0 \Rightarrow \cos A[\cos A - \cos(B - C)] = 0 ⇒ cos A [ cos A − cos ( B − C )] = 0
⇒ cos A [ cos ( B + C ) + cos ( B − C ) ] = 0 \Rightarrow \cos A[\cos(B + C) + \cos(B - C)] = 0 ⇒ cos A [ cos ( B + C ) + cos ( B − C )] = 0
⇒ cos A cos B cos C = 0 \Rightarrow \cos A\cos B\cos C = 0 ⇒ cos A cos B cos C = 0
Thus, either A = 9 0 ∘ A = 90^\circ A = 9 0 ∘ B = 9 0 ∘ B = 90^\circ B = 9 0 ∘ C = 9 0 ∘ C = 90^\circ C = 9 0 ∘ 9 0 ∘ . 90^\circ. 9 0 ∘ .
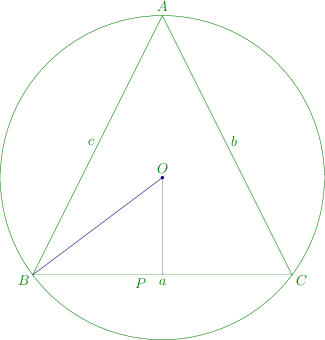
The diagram is given below:
Let O O O A B C . ABC. A BC . O , B O, B O , B C . C. C . R . R. R . △ O B C , \triangle OBC, △ OBC ,
a sin B O C = 2 R ⇒ R = a 2 sin B O C \frac{a}{\sin BOC} = 2R \Rightarrow R = \frac{a}{2\sin BOC} s i n BOC a = 2 R ⇒ R = 2 s i n BOC a
Now since O O O B O BO BO O C OC OC B B B C C C
∠ O B C = B 2 \angle OBC = \frac{B}{2} ∠ OBC = 2 B ∠ O C B = C 2 \angle OCB = \frac{C}{2} ∠ OCB = 2 C
⇒ ∠ B O C = 18 0 ∘ − B 2 − C 2 = 9 0 ∘ + A 2 \Rightarrow \angle BOC = 180^\circ - \frac{B}{2} - \frac{C}{2} = 90^\circ + \frac{A}{2} ⇒ ∠ BOC = 18 0 ∘ − 2 B − 2 C = 9 0 ∘ + 2 A
∴ R = a 2. sin ( 9 0 ∘ + A 2 ) = a 2 sec A 2 \therefore R = \frac{a}{2.\sin\left(90^\circ + \frac{A}{2}\right)} = \frac{a}{2}\sec\frac{A}{2} ∴ R = 2. s i n ( 9 0 ∘ + 2 A ) a = 2 a sec 2 A
The diagram is given below:
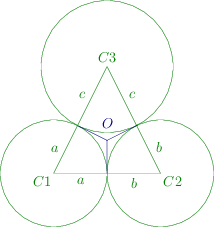
Let the centers of the circle be C 1 , C 2 C_1, C_2 C 1 , C 2 C 3 C_3 C 3 a , b a, b a , b c c c P , Q P, Q P , Q R . R. R . O . O. O .
Since O P OP OP O Q OQ OQ O O O C 3 , C_3, C 3 , O P = O Q OP =
OQ OP = OQ
Similarly, O Q = O R ⇒ O P = O Q = O R OQ = OR \Rightarrow OP=OQ=OR OQ = OR ⇒ OP = OQ = OR
Also, O P ⊥ C 1 C 3 , O Q ⊥ C 2 C 3 OP\perp C_1C_3, OQ\perp C_2C_3 OP ⊥ C 1 C 3 , OQ ⊥ C 2 C 3 O R ⊥ C 1 C 2 OR\perp C_1C_2 OR ⊥ C 1 C 2
Hence, O P , O Q OP, OQ OP , OQ O R OR OR △ C 1 C 2 C 3 . \triangle C_1C_2C_3. △ C 1 C 2 C 3 .
Let O P = O Q = O R = r OP=OQ=OR = r OP = OQ = OR = r 4. 4. 4.
r = Δ s r = \frac{\Delta}{s} r = s Δ s = s = s = △ C 1 C 2 C 3 \triangle C_1C_2C_3 △ C 1 C 2 C 3 Δ = \Delta = Δ = △ C 1 C 2 C 3 \triangle C_1C_2C_3 △ C 1 C 2 C 3
Now, s = ( a + b ) + ( b + c ) + ( c + a ) 2 = a + b + c s = \frac{(a + b) + (b + c) + (c + a)}{2} = a + b + c s = 2 ( a + b ) + ( b + c ) + ( c + a ) = a + b + c
Δ = s ( s − a − b ) ( s − b − c ) ( s − c − a ) = ( a + b + c ) c . a . b \Delta = \sqrt{s(s - a - b)(s - b - c)(s - c - a)} = \sqrt{(a + b + c)c.a.b} Δ = s ( s − a − b ) ( s − b − c ) ( s − c − a ) = ( a + b + c ) c . a . b
r = Δ s = a b c a + b + c = 4 r = \frac{\Delta}{s} = \sqrt{\frac{abc}{a + b + c}} = 4 r = s Δ = a + b + c ab c = 4
⇒ a b c a + b + c = 16 \Rightarrow \frac{abc}{a + b + c} = 16 ⇒ a + b + c ab c = 16
The diagram is given below:
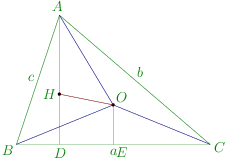
Let R R R △ A B C . \triangle ABC. △ A BC .
A H = 2 O E = 2 R cos A AH = 2OE = 2R\cos A A H = 2 OE = 2 R cos A O A = R OA = R O A = R
∠ B O C = 2 A ∴ ∠ C O E = A ⇒ ∠ O C E = 9 0 ∘ − A \angle BOC = 2A \therefore \angle COE = A \Rightarrow \angle OCE = 90^\circ - A ∠ BOC = 2 A ∴ ∠ COE = A ⇒ ∠ OCE = 9 0 ∘ − A
∴ ∠ O C A = ∠ B C A − ∠ O C E = C − ( 9 0 ∘ − A ) = A + C − 9 0 ∘ \therefore \angle OCA = \angle BCA - \angle OCE = C - (90^\circ - A) = A + C - 90^\circ ∴ ∠ OC A = ∠ BC A − ∠ OCE = C − ( 9 0 ∘ − A ) = A + C − 9 0 ∘
∵ O A = O C ∴ ∠ O A C = ∠ O C A = A + C − 9 0 ∘ \because OA = OC \therefore \angle OAC = \angle OCA = A + C - 90^\circ ∵ O A = OC ∴ ∠ O A C = ∠ OC A = A + C − 9 0 ∘
From △ C D A , ∠ C A D = 9 0 ∘ − C \triangle CDA, \angle CAD = 90^\circ - C △ C D A , ∠ C A D = 9 0 ∘ − C
∴ ∠ H A O = ∠ C A D − ∠ C A O = ( 9 0 ∘ − C ) − ( A + C − 9 0 ∘ ) \therefore \angle HAO = \angle CAD - \angle CAO = (90^\circ - C) - (A + C - 90^\circ) ∴ ∠ H A O = ∠ C A D − ∠ C A O = ( 9 0 ∘ − C ) − ( A + C − 9 0 ∘ )
= 18 0 ∘ − A − 2 C = A + B + C − A − 2 C = B − C = 180^\circ - A - 2C = A + B + C - A - 2C = B - C = 18 0 ∘ − A − 2 C = A + B + C − A − 2 C = B − C
Applying cosine rule in △ A H O , \triangle AHO, △ A H O ,
cos ( B − C ) = A H 2 + A O 2 − O H 2 2 A H . A O \cos(B - C) = \frac{AH^2 + AO^2 - OH^2}{2AH.AO} cos ( B − C ) = 2 A H . A O A H 2 + A O 2 − O H 2
O H 2 = 4 R 2 cos 2 A + R 2 − 2.2 R cos A . R cos ( B − C ) OH^2 = 4R^2\cos^2A + R^2 - 2.2R\cos A.R\cos(B - C) O H 2 = 4 R 2 cos 2 A + R 2 − 2.2 R cos A . R cos ( B − C )
= R 2 [ 4 cos 2 A + 1 − 4 cos A cos ( B − C ) ] = R 2 [ 1 − 4 cos A { cos ( B − C ) − cos A } ] = R^2[4\cos^2A + 1 - 4\cos A\cos(B - C)] = R^2[1 - 4\cos A\{\cos(B - C) - \cos A\}] = R 2 [ 4 cos 2 A + 1 − 4 cos A cos ( B − C )] = R 2 [ 1 − 4 cos A { cos ( B − C ) − cos A }]
= R 2 [ 1 − 4 cos A { cos ( B − C ) + cos ( B + C ) } ] = R^2[1 - 4\cos A\{\cos(B - C) + \cos(B + C)\}] = R 2 [ 1 − 4 cos A { cos ( B − C ) + cos ( B + C )}]
= R 2 [ 1 − 8 cos A cos B cos C ] = R^2[1 - 8\cos A\cos B\cos C] = R 2 [ 1 − 8 cos A cos B cos C ]
O H = R 1 − 8 cos A cos B cos C OH = R\sqrt{1 - 8\cos A\cos B\cos C} O H = R 1 − 8 cos A cos B cos C