The diagram is given below:
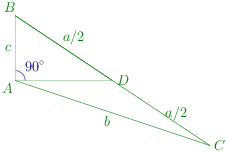
From figure, ∠ADC=90∘+B
By applying m:n rule in triangle ABC, we get
(1+1)cot(90∘+B)=1.cot90∘−1.cot(A−90∘)
−2tanB=0−cot[−(90∘−A)]
−2tanB=tanA⇒tanA+2tanB=0
Given, cotA+cotB+cotC=3
Squaring, cot2A+cot2B+cot2C+2cotAcotB+2cotBcotC+2cotCcotA=3
Since A+B+C=π⇒A+B=π−C
cot(A+B)=cot(π−C)
cotA+cotBcotAcotB−1=−cotC
cotAcotB+cotBcotC+cotCcotA=1
⇒cot2A+cot2B+cot2C+2cotAcotB+2cotBcotC+2cotCcotA=3(cotAcotB+cotBcotC+cotCcotA)
21[(cotA−cotB)2+(cotB−cotC)2+(cotC−cotA)2]=0
⇒cotA=cotB=cotC
⇒A=B=C i.e. triangle is equilateral.
Given, (a2+b2)sin(A−B)=(a2−b2)sin(A+B)
(sin2A+sin2B)sin(A−B)=(sin2A−sin2B)sin(A+B)
[∵sin2A−sin2B=sin(A+B)sin(A−B)]
⇒(sin2A+sin2B)sin(A−B)=sin2(A+B)sin(A−B)
⇒sin(A−B)[sin2A+sin2B−sin2C]=0
Either sin(A−B)=0 or sin2A+sin2B−sin2C=0
A=B or a2+b2−c2=0
Thus, triangle is either isosceles or right angled.
R.H.S. =c(cosAcosθ+sinAsinθ)+a(cosCcosθ−sinCsinθ)
=cosθ(ccosA+acosC)+sinθ(csinA−asinC)
=bcosθ+sinθ(c.2Ra−a.2Rc)
=bcosθ= L.H.S.
The diagram is given below:
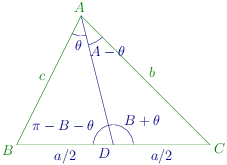
sin(B+θ)b=2sin(A−θ)a
sin[π−(B+θ)]c=2sinθa
⇒bsin(A−θ)=csinθ
⇒sinB(sinAcosθ−cosAsinθ)=sinCsinθ=(sinAcosB+sinBcosA)sinθ
⇒cotθ=2cotA+cotB
The diagram is given below:
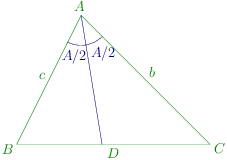
ΔABC=ΔABD+ΔACD
21bcsinA=21AD.csin2A+21AD.bsin2A
⇒AD=b+c2bccos2A
The diagram is given below:
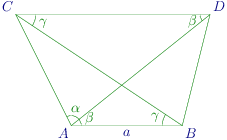
∠ACB=π−(α+β+γ)
sinACB=sin(α+β+γ)
In △ABC
sinACBAB=sinγAC
AC=sin(α+β+γ)asinγ
In △ACD
sinαCD=sinβAC
CD=sinβsin(α+β+γ)asinαsinγ
Given, 2cosA=sinCsinB
2cosAsinC=sinB=sin[π−(A+C)]=sin(A+C)
2cosAsinC=sinAcosC+cosAsinC
cosAsinC=sinAcosC⇒tanA=tanC
⇒A=C
Thus, the triangle is isosceles.
Let such angles be A and B. Then,
cosA=a1 and cosB=b1
⇒sinAcosA=sinBcosB
sin2A=sin2B or sin2A=sin[π−2B]
A=B or A+B=2π⇒C=2π
Thus, the triangle is either isosceles or right angled.
Given atanA+btanB=(a+b)tan2A+B
⇒a(cosAsinA−cos2A+Bsin2A+B)=b(cos2A+Bsin2A+B−cosBsinB)
⇒a.cosAcos2A+Bsin2A−B=b.cosBcos2A+Bsin2A−B
⇒tanA=tanB⇒A=B
Thus, the triangle is isosceles.
Given, tanA+tanBtanA−tanB=cc−b
⇒cosAsinA+cosBsinBcosAsinA−cosBsinB=sinCsinC−sinB
⇒sinAcosB+sinBcosAsinAcosB−sinBcosA=sin(A+B)sin(A+B)−sinB
⇒sin(A+B)sinAcosB−sinBcosA=sin(A+B)sin(A+B)−sinB
⇒sinAcosB−sinBcosA=sinAcosB+sinBcosA−sinB
⇒sinB=2sinBcosA⇒cosA=21⇒A=60∘.
We know that cosC=2aba2+b2−c2
Given, c4−2(a2+b2)c2+a4+a2b2+b4=0
⇒a4+b4+c4−2a2c2−2b2c2+2a2b2=a2b2
(a2+b2−c2)2=a2b2⇒a2+b2+c2=±ab
⇒cosC=±21⇒A=60∘ or 120∘
Given, cosA+2cosBcosA+2cosC=sinCsinB
⇒cosA(sinC−sinB)=2sinBcosB−2sinCcosC=sin2B−sin2C
⇒2cosA.cos2B+Csin2C−B=2cos(B+C)sin(B−C)
cosA.cos2B+Csin2C−B=−2cosA.sin2B−C.cos2B−C
If B=C then above it 0=0 i.e. triangle is isosceles.
If A=90∘ then above is 0=0 i.e. triangle is right angled.
∵tan2A,tan2B,tan2C are in A.P.
tan2A−tan2B=tan2B−tan2C
cos2Acos2Bsin(2A−2B)=cos2Bcos2Csin(2B−2C)
sin(2A−2B)cos2C=sin(2B−2C)cos2A
sin(2A−2B)sin(2A+2B)=sin(2B−2C)sin(2B+2C)
⇒cosB−cosA=cosC−cosB
Thus, cosA,cosB,cosC are in A.P.
Given, acos22C+ccos22A=23b
a.abs(s−c)+c.bcs(s−a)=23b
bs[2s−a−c]=23b
2s=3b⇒a+c=2b
We have to prove that cot2A+cot2C=2cot2B
L.H.S. =Δs(s−a)+Δs(s−c)
=Δs(2s−a−c)=Δ2s(s−b)=2cot2B= R.H.S.
Given, a2,b2,c2 are in A.P.
⇒b2−a2=c2−b2
⇒sin2B−sin2A=sin2C−sin2B
⇒sin(B+A)sin(B−A)=sin(C+B)sin(C−B)
⇒sinCsin(B−A)=sinAsin(C−B)
⇒sinAsinBsinAcosB−cosBsinA=sinBsinCsinBcosC−sinCcosB
⇒cotB−cotA=cotC−cotB
∴cotA,cotB,cotC are in A.P.
Since A,B,C are in A.P. ⇒2B=A+C⇒A+B+C=3B=180∘⇒B=60∘
Given, 2b2=3c2
2.sin2B=3.sin2C⇒sinC=±21
sinC=−21 because C<120∘
sinC=21⇒C=45∘
⇒A=75∘
Given, tan2A,tan2B,tan2C are in H.P.
⇒cot2A,cot2B,cot2C are in A.P.
cot2B−cot2A=cot2C−cot2B
Δs(s−b)−s(s−a)=Δs(s−c)−s(s−b)
a−b=b−c
a,b,c are in A.P.
Given, sinCsinA=sin(B−C)sin(A−B)
sinCsinA=sinBcosC−sinCcosBsinAcosB−sinBcosA
sinAsinCcosC+sinBsinCcosA=2sinAsinCcosB
sinBsin(A+C)=2sinAsinCcosB
sin2B=2sinAsinCcosB
cosB=2acb2=2aca2+c2−b2
⇒c2+a2=2b2
Thus, a2,b2,c2 are in A.P.
Given, 2sinB=sinA+sinC
4sin2Bcos2B=2sin2A+Ccos2A−C=2cos2Bcos2A−C
2sin2B=3cos2A+C=cos2A−C
3sin2Asin2C=cos2Acos2C
3tan2Atan2C=1
Given, a2,b2,c2 are in A.P.
b2−a2=c2−b2
sin2B−sin2A=sin2C−sin2B
sin(A+B)sin(A−B)=sin(B+C)sin(B−C)
sinCsin(A−B)=sinAsin(B−C)
cosB−cotAsinB=sinBcotC−cosB
2cosB=sinB(cotA+cotC)
2cotB=cotA+cotC
∴cotA,cotB,cotC are in A.P.
∴tanA,tanB,tanC are in H.P.
We have proven in previous problem that ∴cotA,cotB,cotC are in A.P.
Since A,B,C are in A.P. ⇒2B=A+C⇒A+B+C=3B=180∘⇒B=60∘
b:c=3:2⇒sinC=23.32=21
⇒C=45∘⇒A=75∘
Let the sides are a,b,c then 2b=a+c. Also, let a to be greatest and c to be smallest
side.
Then, A=90+C then 90+C+B+C=180⇒B=90−2C
sin(90+C)a=sin(90−2C)b=sinCc=2R
4Rcos2C=2RcosC+2RsinC
2cos2C=cosC+sinC
Squaring, we get
4(1−sin22C)=1+sin2C⇒sin2C=43 when 1+sin2C=0
When 1+sin2C=0⇒C=43π which is not possible.
∵sin2C=43⇒cos2C=47
Now sinC and cosC can be found and ratio can be evaluated.
∵a,b,c are in A.P. 2b=a+c⇒a=2b−c
cosA=2bcb2+c2−a2=2bcb2+c2−4b2−c2+4bc
=2bc4bc−3b2=2c4c−3b
The diagram is given below:
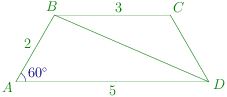
Let AB=2,AD=5,BC=3 annd CD=x
Since it is cyclic quadrilateral ∠C=120∘
Applying cosine rule in ΔABD, we have
cos60∘=2.AB.ADAB2+AD2−BD2⇒BD2=19
Applying cosine rule in ΔBCD, we have
cos120∘=2.BC.BDBC2+CD2−BD2⇒x2+3x−10=0
x=−5,2 but x cannot be -ve. ∴x=2
Given (a+b+c)(b+c−a)=3bc
b2+c2−a2+2bc=3bc
2bcb2+c2−a2=21
cosA=cos60∘
A=60∘
Since AD is the median
∴AB2+AC2=2BD2+2AD2
⇒b2+c2=4a2+2AD2
4AD2=b2+c2+(b2+c2−a2)
cosA=21=2bcb2+c2−a2
⇒4AD2=b2+c2+bc
The diagram is given below:
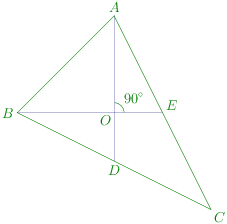
Since AD is the median
∴AB2+AC2=2BD2+2AD2
⇒AD2=42b2+2c2−a2
AO=32AD=32.212b2+2c2−a2
Similalry BO=312c2+2a2−b2
∵∠AOB=90∘
∴AO2+BO2=AB2
⇒a2+b2=5c2
Given, 1tanA=2tanB=3tanC=k
Since A,B,C are the angles of a triangle
∴tanA+tanB+tanC=tanAtanBtanC
k+2k+3k=k.2k.3k⇒k=1 as if k=−1 sum of angles will be greater than 180∘.
tanA=1⇒sinA=21
tanA=2⇒sinA=52
tanA=3⇒sinA=103
sinAa=sinBb=sinCc
2a=25b=310c
62a=35b=210c
For a triangle sides are positive i.e. a>0,b>0,c>0 where a,b,c are the sides.
2x+1>0⇒x>−21
x2−1>0⇒x>1 because side cannot be negative.
x2+x+1>0 ∀x>1
a−b=x(x−1)>0⇒a>b
a−c=x+2>0⇒a>c
Hence a is the greatest side.
cosA=2bcb2+c2−a2=2(2x+1)(x2−1)(2x+1)2+(x2−1)2−(x2+x+1)
=−21
⇒A=120∘
Let the sides be x,x+1,x+2 where x>0 and is a natural number. Let the smallest angle be θ
∠C=θ∴∠A=2θ
Applying sine law
sinθx=sin(π−3θ)x+1=sin2θx+2
⇒sinθx=sin2θx+2⇒2cosθ=xx+2
⇒sinθx=sin3θx+1=3sinθ−4sin2θx+1
⇒3−4sin2θ=xx+1
⇒4cos2θ=x2x+1=x2(x+2)2
⇒x2−3x−4=0
x=4,−1 but −1 is not a natural number so x=4. Hence sides are 4,5,6.
Given, a=6 cm, Δ=12 sq. cm. and B−C=60∘
Δ=21absinC=21a.ksinBsinC
=21.a.sinAasinBsinC
Δ=21a2sinBsinC=sinA18sinBsinC
⇒32=2sinA2sinBsinC=2sinAcos(B−C)−cos(B+C)
⇒32=2sinAcos60∘−cos(π−A)
⇒8sinA−6cosA=3
Given, cosθ=b+ca⇒1+cosθ=b+ca+b+c
⇒2cos22θ=b+ca+b+c
sec22θ=a+b+c2(b+c)
1+tan22θ=a+b+c2(b+c)
Similarly, 1+tan22ϕ=a+b+c2(c+a)
and 1+tan22ψ=a+b+c2(a+b)
Adding, we get 3+tan22θ+tan22ϕ+tan22ψ=a+b+c4(a+b+c)
⇒tan22θ+tan22ϕ+tan22ψ=1
Since C is the angle of a triangle, sinC≤1
∴cosAcosB+sinAsinB≥cosAcosB+sinAsinBsinC
⇒cos(A−B)≥1
But cos(A−B) cannot be greater than 1.∴cos(A−B)=1⇒A=B
Now, cosAcosB+sinAsinBsinC=1
⇒cos2A+sin2AsinC=1
⇒sinC=1⇒C=90∘⇒A=B=45∘
⇒a:b:c=sinA:sinB:sinC=1:1:2
From the question, sinAsinBsinC=p and cosAcosBcosC=q
∴tanAtanBtanC=qp
Since we are dealing with a triangle ∴tanA+tanB+tanC=tanAtanBtanC
⇒tanA+tanB+tanC=1p
Now, tanAtanB+tanBtanC+tanCtanA=cosAcosBcosCsinAsinBcosC+sinBsinCcosA+sinAsinCcosB
[ We know that in a triangle 2sinAsinBcosC=sin2A+sin2B−sin2C ]
⇒2q1[(sin2A+sin2B−sin2C)+(sin2B+sin2C−sin2A)+(sin2C+sin2A−sin2B)]
=2q1[sin2+sin2B+sin2C]
=2q1[2(1−cos2A)+(1−cos2B)+(1−cos2C)]
=4q1[4+4cosAcosBcosC]=q1+q
Thus, we see that tanA,tanB,tanC are roots of the given equation.
Given, sin3θ=sin(A−θ)sin(B−θ)sin(C−θ)
4sin3θ=2sin(A−θ)[2sin(B−θ)sin(C−θ)]
=2sin(A−θ)[cos(B−C)−cos(B+C−2θ)]
=2sin(A−θ)cos(B−C)−2sin(A−θ)cos(B+C−2θ)
=sin(A+B−C−θ)+sin(A+C−θ−B)−sin(A+B+C−3θ)+sin(π−2B−θ)
sin3θ+4sin3θ=sin(2A+θ)+sin(2B+θ)+sin(2C+θ)
3sinθ=(sin2A+sin2B+sin2C)cosθ+(cos2A+cos2B+cos2C)sinθ
[ ∵sin2A+sin2B+sin2C=4sinAsinBsinC when A+B+C=π ]
(1−cos2A)+(1−cos2B)+(1−cos2C)sinθ=4sinAsinBsinC.cosθ
2[(sin2A+sin2B+sin2C)sinθ]=4sinAsinBsinCcosθ
2sinθ[(sin2A+sin2B−sin2C)+(sin2B+sin2C−sin2A)+(sin2C+sin2A−sin2B)]=4sinAsinBsinCcosθ
[ ∵sin2+sin2B−sin2C=2sinAsinBcosC ]
⇒cotθ=cotA+cotB+cotC
From question cb=r∴b=cr
Let AD⊥BC and let AD=h
We have to prove that h≤1−r2ar
ΔABC=21c.cr.sinA=21ah
h=ac2rsinA
cosA=2.c.crc2+c2r2−a2
c2=1+r2−2rcosAa2
⇒h=a(1+r2−2rcosa)a2rsinC=1+r2−2rcosAarsinA
=1+r2−2r1+tan22A1−tan22Aar.1+tan22A2tan2A
⇒(1+r2)tan22A−h2artan2A+(1−r)2=0
This is a quadratic equation in tan2A and since it will be read D≥0
⇒h24a2r2−4(1+r)2(1−r)2≥0
h≤1−r2ar
Given b.c=k2, now
cosA=2bcb2+c2−a2⇒2k2cosA=b2+b2k4−a2
b4−(a2+2k2cosA)b2+k4=0 which is a quadratic equation in b2.
The triangle will not exists if discriminant is less than zero for above equation because then b will become a complex
number.
⇒(a2+2k2cosA)2−4k4<0
⇒[a2+2k2(1+cosA)][a2−2k2(1−cosA)]<0
⇒(a2+4k2cos22A)(a2−4k2sin23A)<0
⇒a2−4k2sin22A,0[∵a2+2k2cos22A>0]
⇒(a+2ksin2A)(a−2ksin2A)<0
⇒a−2ksin2A<0[∵]a+2ksin2A>0]
⇒a<2ksin2A
The diagram is given below:
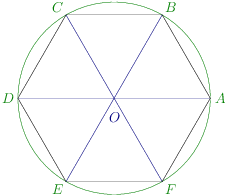
The diagram is a top view. Let O be the top point and O′ the center of ring which is 12 cm below
O in the diagram(not shown).
In triangle OO′A,AO′=5 cm, OO′=12 cm
AO=122+52=13 cm
Now sides of a regular hexagon are equal to the circumscribing circle. AB=5 cm.
cosAOB=2.13.13132+132−52=338313
Given, 2b=3a and tan22A=53
cosA=1+tan22A1=1+531=85
cosA=85=2bcb2+c2−a2
=2bcb2+c2−94b2
⇒98(5b2+9c2)=25bc
⇒98c2−185bc+58b2=0
⇒c=6885,6845
Thus, one value is double of the other.
Let the angles are k,2k,7k degrees. Then k+2k+7k=180∘⇒k=18∘
So greatest angle is 126∘ and smallest is 18∘.
Ratio of greatest to least side is given by sin126∘;;sin18∘
=cos36∘:sin18∘=5+1:5−1
Let AF=f,BG=g,CH=h
Area of △ABC= Area of △ABF + Area of △ACF
21bcsinA=21.2sin2Acos2A=2cf1sin2A+21bfsin2A
⇒2bccos2A=(b+c)f
f1cos2A=21(b1+c1)
Similarly, g1cos2B=21(a1+c1)
and, h1cos2C=21(a1+b1)
Adding these three we obtain desired result.
Since BD=DE=EC each will be equal to 35. Clearly the triangle is right angled because 32+52=52
cosC=54
In △ACE,cosC=2.CE.4CE2+42−AE2=2.35.4925+16−AE2
⇒9169−9AE2.403=54
⇒AE2=973
cosθ=2.AE.ACAE2+AC2−CE2=738
tanθ=sec2θ−1=6473−1=83
Let O be the centroid i.e. point of intersection of medians.
From geometry, we know that area of △ABC=3× area of △AOC
We also know that centroid divides median in the ratio of 2:1 i.e. AO=310
Applying sine rule in △AOC
sin8πOC=sin4πAO
OC=310sin4πsin8π
Area of △AOC=21AO.OCsinAOC
=21310.310.sin4πsin8πsin(2π+8π)
=925
∴ΔABC=975.
Let sides are a,b,c then a=7=49 cm, b=43=48 cm and c=13
cm.
Clearly, c is smallest and thus C will be smallest.
cosC=2.7.4348+49−13=23
⇒C=30∘
Let the triangle be ABC having right angle at C. Let D be the mid-point of AC.
Given that triangle is isoceles so AC=BC i.e. DC=21AC=21BC
Also, ∠CAB=∠BDA=45∘
Let ∠DBC=θ and ∠DBA=ϕ
tanϕ=BCDC=21
tanϕ=tan(45∘−θ)=1+tanθ1−tanθ
⇒tanϕ=31
∴cotθ=2,cotϕ=3
From the given ratios we have,
(1+m2)(1+n2)a+b=(1−m2)(1−n2)a−b=(1−m2)(1+n2)c
⇒ca+b=1−m21+m2,ca−b=1+n21−n2
⇒cos2A+Bcos2A−B=1−m21+m2,sin2A+Bsin2A−B=1+n21−n2
By componendo and dvidendo, we have
tan2Atan2B=m2,cot2Atan2B=n2
⇒tan22A=n2m2,tan22B=m2n2
⇒A=2tan−1nm,B=2tan−1mn
Δ=21bcsinA=21bc1+tan22A2tan2A
=m2+n2mnbc
Since a,b,c are roots of the equation x3−px2+qx−r=0 therefore we have
a+b+c=p=2s where s is perimeter.
ab+bc+ca=q and abc=r
Δ2=s(s−a)(s−b)(s−c)
=2p(2p−a)(2p−b)(2p−c)
Substituting the values of we obtain the desired result.
Let the third side be a cm. Applying cosine rule,
6=a2+42−2.a.4cos30∘
a2−43a+10=0
a=243±48−40=23±2
Both roots are positive, so two such triangles are possible.






